
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems to get into Exercises on the Z Transform.
So, without further ado, let's dive straight into it!
Z Transform and ROC Examples [Based on 22.4 from Ref1]
Let's determine the Z Transform, pole-zero plot and associated ROC for each of the following cases:

a.
The signal x1[n] is a common case, which is included in Z Transform tables. As such, it has a well-known Z Transform and ROC, which is given by:
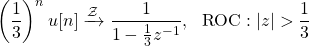
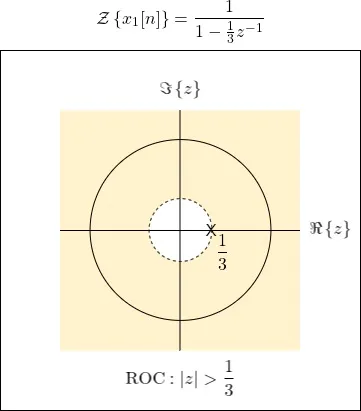
The root of the denominator is a pole, and at point 1/3 in the real-axis. So, at last, the pole-zero plot and ROC can be visualized as follows:
b.
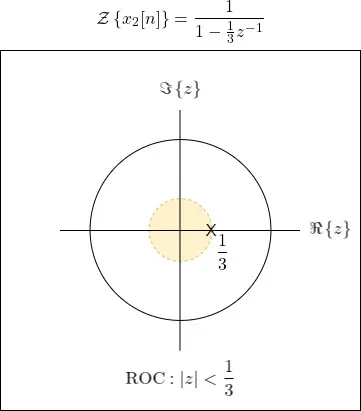
The second signal, x2[n] has the same exact algebraic expression for the Z Transform. The only difference is the ROC, which is now the inner circle. So, the Z Transform and ROC are as follows:

And visually we have:
ROC from Conditions [Based on 22.3 from Ref1]
Let's consider the following pole-zero plot of the Z Transform X(z) of a sequence x[n]:

Determine the associated region of convergence (ROC) for each of the following conditions:
- x[n] is right-sided
- x[n] is left-sided
- The Fourier transform of x[n] converges
- The Fourier transform of x[n] doesn't converge
1.
For a signal to be right-sided, the ROC must be of the form |z| > a. And, since the ROC can't include poles the ROC is:
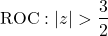
2.
Now, for it to be left-sided, it's ROC must be of the form |z| < a, and not include poles, which leads to:
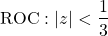
3.
In order to converge, the ROC must include the unit circle (|z| = 1). And, because it must be bounded by poles, the ROC can only be:
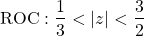
4.
For the FT of x[n] to not converge, the ROC must not contain the unit circle, which means that there are two possibilities:
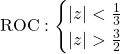
LTI System Analysis Example
Consider a discrete-time LTI system, with the following transfer function:
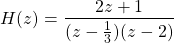
Let's specify and sketch the ROC (and pole-zero plot) for each of the following cases:
- The system is causal
- The system is stable
Poles and Zeros
First of all, in any of these cases the corresponding poles and zeros are as follows:
- The root of the numerator polynomial z = - 1/2 is a zero.
- The roots of the denominator polynomial z = 1/3 and z = 2 are the poles.
This leads to the following pole-zero diagram, which will be shared amongst the follow-up cases:

1. Causal
As we know, a system is causal when the ROC is the outside region of a circle. In the case of rational functions it must also be:
- outside of the most distant pole, and
- the degree of the numerator must not be larger then the degree of the denominator polynomial
So, in the case of this system, the ROC is:

or graphically:

2. Stable
For a system to be stable, the ROC must simply contain the unit circle.
As such, the ROC can be either of the following:

and so either the complete z-region, the region below the circle at 2 or the intermediate region of two circles (one at 1/3 and one at 2).
Graphically:

Let's note that it's impossible for this system to be both causal and stable!
RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io
Previous articles of the series
Basics
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
LTI Systems and Convolution
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Exercises on LTI System Properties → Superposition, Impulse Response and System Classification Examples
- Exercise on Convolution → Discrete-Time Convolution Example with the help of visualizations
- Exercises on System Representation using Difference Equations → Simple Block Diagram to LCCDE Example, Direct Form I, II and LCCDE Example
- Exercises on System Representation using Differential Equations → Equation to Block Diagram Example, Direct Form I to Equation Example
Fourier Series and Transform
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
- Continuous-Time Fourier Transform Properties → Linearity, Time-Shifting (Translation), Conjugate Symmetry, Time and Frequency Scaling, Duality, Differentiation and Integration, Parseval's Relation, Convolution and Multiplication Properties
- Discrete-Time Fourier Series & Transform → Getting into Discrete-Time, Fourier Series and Transform, Synthesis and Analysis Equations
- Discrete-Time Fourier Transform Properties → Differences with Continuous-Time, Periodicity, Linearity, Time and Frequency Shifting, Conjugate Summetry, Differencing and Accumulation, Time Reversal and Expansion, Differentation in Frequency, Convolution and Multiplication, Dualities
- Exercises on Continuous-Time Fourier Series → Fourier Series Coefficients Calculation from Signal Equation, Signal Graph
- Exercises on Continuous-Time Fourier Transform → Fourier Transform from Signal Graph and Equation, Output of LTI System
- Exercises on Discrete-Time Fourier Series and Transform → Fourier Series Coefficient, Fourier Transform Calculation and LTI System Output
Filtering, Sampling, Modulation, Interpolation
- Filtering → Convolution Property, Ideal Filters, Series R-C Circuit and Moving Average Filter Approximations
- Continuous-Time Modulation → Getting into Modulation, AM and FM, Demodulation
- Discrete-Time Modulation → Applications, Carriers, Modulation/Demodulation, Time-Division Multiplexing
- Sampling → Sampling Theorem, Sampling, Reconstruction and Aliasing
- Interpolation → Reconstruction Procedure, Interpolation (Band-limited, Zero-order hold, First-order hold)
- Processing Continuous-Time Signals as Discrete-Time Signals → C/D and D/C Conversion, Discrete-Time Processing
- Discrete-Time Sampling → Discrete-Time (or Frequency Domain) Sampling, Downsampling / Decimation, Upsampling
- Exercises on Filtering → Filter Properties, Type and Output
- Exercises on Modulation → CT and DT Modulation Examples
- Exercises on Sampling and Interpolation → Graphical/Visual Sampling and Interpolation Examples
Laplace and Z Transforms
- Laplace Transform → Laplace Transform, Region of Convergence (ROC)
- Laplace Transform Properties → Linearity, Time- and Frequency-Shifting, Time-Scaling, Complex Conjugation, Multiplication and Convolution, Differentation in Time- and Frequency-Domain, Integration in Time-Domain, Initial and Final Value Theorems
- LTI System Analysis using Laplace Transform → System Properties (Causality, Stability) and ROC, LCCDE Representation and Laplace Transform, First-Order and Second-Order System Analysis
- Exercises on the Laplace Transform → Laplace Transform and ROC Examples, LTI System Analysis Example
- Z Transform → Z Transform, Region of Convergence (ROC), Inverse Z Transform
- Z Transform Properties → Linearity, Time-Shifting, Time-Scaling, Time-Reversal, z-Domain Scaling, Conjugation, Convolution, Differentation in the z-Domain, Initial and Final value Theorems
- LTI System Analysis using Z Transform → System Properties (Causality, Stability), LCCDE Representation and Z Transform
Final words | Next up
And this is actually it for today's post!
From next time on, we will start getting into other various topics related to the Laplace and Z Transform...
See Ya!

Keep on drifting!

