
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems in order to cover Exercises on LTI System Properties.
So, without further ado, let's dive straight into it!
Discrete-Time Superposition [Based on P4.1 from Ref1]
Let's start simple by considering a discrete-time linear system with outputs y[n] and inputs x[n], as shown in the following Figure.
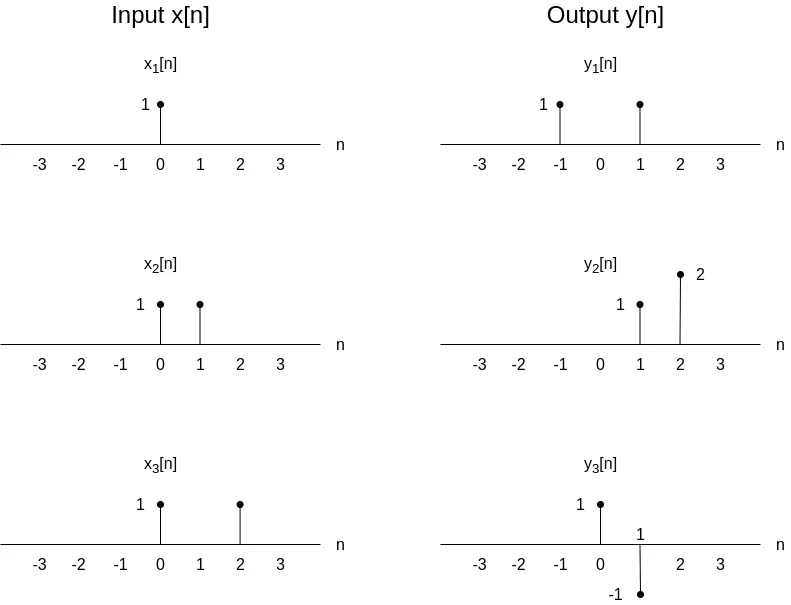
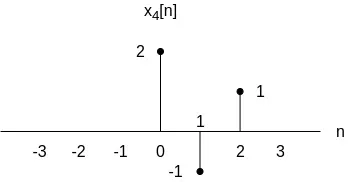
What is the response of the system, y4[n], for the following input:
Solution
We know that the system is linear, which means that is satisfies the principle of superposition:

As such, in order to find the response of the system for the given input x4[n], we shall first express it as a linear combination of x1[n], x2[n] and x3[n].
After that, the response can be easily calculated using the same "alloying" of the output.
One linear combination that we can come up with is the following:

which can be easily proofed as such:

Using superposition, the system response is:

which means that:
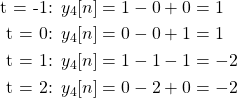
and so the response y4[n] can be visualized as such:

Discrete-Time System using Difference Equation Representation [Based on P5.2 from Ref1]
Consider a discrete-time system that is described by the following first-order difference equation:

Let's verify that the impulse response h[n] is equal to the unit step function u[n] and check if the system satisfies the memory-less, causal and stable properties.
Solution
In order to find the impulse response y[n] = h[n] of a given system, the impulse input x[n] = δ[n] is applied to the system.
Substituting these results in the following equation:
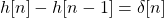
which can only be satisfied if h[n] = u[n].
For a system to be static (memory-less) the output has to only depend on present/current input.
In the case of this system y[0] is calculated as such:

where in turn the previous response y[-1] requires the previous input x[-1], and so the system is not memory-less.
Next up is causality. For a system to be causal the response has to only depend on present and past input, and not future input. This is of course satisfied in the case of this system, making the system causal.
Lastly, let's see if the system is stable. A system is stable when bounded input leads to bounded output, where bounded basically means that the signal has finite amplitude. The impulse response h[n] is equal to the unit step function u[n], which is a bounded signal. And so, the system can also be classified as stable.
Continuous-Time System using Differential Equation Representation [Based on P5.3 from Ref1]
Suppose a continuous-time system that is described by the following first-order differential equation:
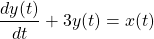
Let's verify that the impulse response is equal to h(t) = e-3tu(t) and then check if the system can be classified as memory-less, causal or stable.
Solution
Substituting h(t) with the given impulse response, the derivative of h(t) is:
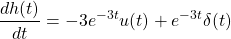
and so:
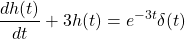
The right-hand side and δ(t) give the same result when within an integral, which means that the impulse response is correct.
The system is not memory-less, because the impulse response h(t) is not a multiple of δ(t), but the system is causal as h(t) is 0 for t < 0.
Lastly, the system is also stable, because h(t) is absolutely integrable:

RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io
Previous articles of the series
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
- Continuous-Time Fourier Transform Properties → Linearity, Time-Shifting (Translation), Conjugate Symmetry, Time and Frequency Scaling, Duality, Differentiation and Integration, Parseval's Relation, Convolution and Multiplication Properties
- Discrete-Time Fourier Series & Transform → Getting into Discrete-Time, Fourier Series and Transform, Synthesis and Analysis Equations
- Discrete-Time Fourier Transform Properties → Differences with Continuous-Time, Periodicity, Linearity, Time and Frequency Shifting, Conjugate Summetry, Differencing and Accumulation, Time Reversal and Expansion, Differentation in Frequency, Convolution and Multiplication, Dualities
Final words | Next up
And this is actually it for today's post!
Next time we will get into exercises on other topics that we covered!
See Ya!

Keep on drifting!

