
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems in order to cover the Laplace Transform.
So, without further ado, let's dive straight into it!
Getting into the Laplace Transform
Up to this point in the series linear time-invariant (LTI) system analysis has been based on the properties of Fourier analysis.
The properties of this Fouriers analysis are a direct consequence of representing signals as linear combinations of basic signals.
Choosing the eigenfunctions of LTI systems to be of the form  led to the Fourier transform synthesis equation.
And using this representation any given LTI system can be represented by the spectrum of eigenvalues as a function of ω, which is basically the ampltiude change that the system applied to each of those basic inputs.
led to the Fourier transform synthesis equation.
And using this representation any given LTI system can be represented by the spectrum of eigenvalues as a function of ω, which is basically the ampltiude change that the system applied to each of those basic inputs.


But, the Fourier transform comes with restrictions.
Thus, in order to generalize the Fourier transform for a broader class of signals and systems that it doesn't converge to, the Laplace transform was born.
The Laplace transform is using eigenfunctions which are complex exponentials of the form  , where s is a complex number.
Using this more general class allows for the representation of signals and systems in terms of the Laplace transform.
The response of an LTI system to a complex exponential of the form
, where s is a complex number.
Using this more general class allows for the representation of signals and systems in terms of the Laplace transform.
The response of an LTI system to a complex exponential of the form  is
is  .
.
 represents the change in amplitude, and is referred to as the system function.
In other words,
represents the change in amplitude, and is referred to as the system function.
In other words,  is the Laplace transform of the system impulse response.
is the Laplace transform of the system impulse response.
Of course the Laplace and Fourier transform are closely related to each other.
The variable s can be thought of as 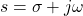 .
Therefore, when s is purely imaginary or
.
Therefore, when s is purely imaginary or  , the Laplace transform is basically reduced to the Fourier transform.
So, the Laplace transform is the Fourier transform of a signal after an exponential weighting of
, the Laplace transform is basically reduced to the Fourier transform.
So, the Laplace transform is the Fourier transform of a signal after an exponential weighting of  has been applied.
Because of that, the Laplace transform converges for signals for which the Fourier transform does not converge.
has been applied.
Because of that, the Laplace transform converges for signals for which the Fourier transform does not converge.
Laplace Transform
The Laplace transform is used for continuous-time signals and systems. Mathematically, the following changes can be applied to Fourier transform equation:
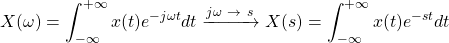
Similar to the Fourier transform the Laplace transform is also represented mathematically using the first letter in its name, which is L, and as such:

Using the Laplace transform, the impulse response (system response for complex exponential) is:

Using the definition of s as 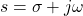 , we can re-write the equation of the Laplace transform as follows:
, we can re-write the equation of the Laplace transform as follows:

As such, the Laplace transform is basically the Fourier transform of  , or mathematically:
, or mathematically:
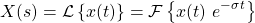
This also explains why one might converge, whilst the other may not.
Example
Let's take the commonly used exponential:

as an quick example.
From the Fourier transform pairs, we know that its Fourier transform is:

We changed the notation in order to make it easier to relate the Fourier transform with the Laplace transform, meaning that now:

Well, because 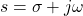 , when
, when  , the Laplace transform is similar and simply:
, the Laplace transform is similar and simply:

With this example we quietly introduced the concept of convergence.
Region of Convergence (ROC)
From what we saw up to this point, the Laplace transform is a function of a general complex variable s, which converges for a range of values. This range is referred to as the region of convergence (ROC) and is very important in associating the Laplace transform with a given signal. When talking about the Fourier transform any given signal had a unique algebraic expression, but in the case of the Laplace transform two different signals might have an identical algebraic expression, but differ at the ROC. So, in the case of the Laplace transform a signal is represented by both its mathematical expression and the range of values for which s is valid.
An easy way to deal with signals when using the Laplace transform is by representing them as a ratio of polynomials.

The roots of the numerator, 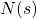 , are the zeros of the Laplace transform, whilst the roots of the denominator,
, are the zeros of the Laplace transform, whilst the roots of the denominator,  , are the poles.
That way its convenient to represent the Laplace transform in the complex s-plane, putting X's in the locations of poles and O's in the locations of zeroes.
This pole-zero diagram can help specify the algebraic expression for the Laplace transform.
Of course, the ROC must also be known.
, are the poles.
That way its convenient to represent the Laplace transform in the complex s-plane, putting X's in the locations of poles and O's in the locations of zeroes.
This pole-zero diagram can help specify the algebraic expression for the Laplace transform.
Of course, the ROC must also be known.
We have three choices for the ROC, which are:
- The ROC contains no poles,

- The ROC of
 consists of a strip parallel to the jω-axis in the s-plane
consists of a strip parallel to the jω-axis in the s-plane - The Fourier transform of
 converges and so ROC includes the jω-axis in the s-plane
converges and so ROC includes the jω-axis in the s-plane
Example
Let's consider the Laplace transform expression:

All three of the following pole-zero diagrams (and the ROC's they correspond to) are valid representations:

Some additional useful rules and properties:
- For signals of finite duration, the ROC is mostly the entire s-plane
- For right-sided signals with
 in the ROC, all values greater than σ0 are also in the ROC. When
in the ROC, all values greater than σ0 are also in the ROC. When  is rational, the ROC is basically to the right of the rightmost pole.
is rational, the ROC is basically to the right of the rightmost pole. - Similarly, for left-sided signals with
 in the ROC all values less than σ0 are also in the ROC, and when rational the ROC is to the left of the leftmost pole.
in the ROC all values less than σ0 are also in the ROC, and when rational the ROC is to the left of the leftmost pole. - For two-sides signal with
 in the ROC, the ROC is a strip in the s-plane.
in the ROC, the ROC is a strip in the s-plane.
Sometimes its easier to specify the Laplace by decomposing it into a partial fraction expansion.
For example, in the case of  from the previous example:
from the previous example:

Using such properties its sometimes easy to identify the ROC directly from the pole-zero pattern in the s-plane. Of course auxilary information about the signal in the time-domain has to also be known, like if the signal is right-sided, left-sided or two-sided. But, either way, the relation of the poles of the Laplace transform with certain properties of the signal in the time-domain are very important to include, while doing LTI system analysis using the Laplace transform.
RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io and GeoGebra
Previous articles of the series
Basics
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
LTI Systems and Convolution
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Exercises on LTI System Properties → Superposition, Impulse Response and System Classification Examples
- Exercise on Convolution → Discrete-Time Convolution Example with the help of visualizations
- Exercises on System Representation using Difference Equations → Simple Block Diagram to LCCDE Example, Direct Form I, II and LCCDE Example
- Exercises on System Representation using Differential Equations → Equation to Block Diagram Example, Direct Form I to Equation Example
Fourier Series and Transform
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
- Continuous-Time Fourier Transform Properties → Linearity, Time-Shifting (Translation), Conjugate Symmetry, Time and Frequency Scaling, Duality, Differentiation and Integration, Parseval's Relation, Convolution and Multiplication Properties
- Discrete-Time Fourier Series & Transform → Getting into Discrete-Time, Fourier Series and Transform, Synthesis and Analysis Equations
- Discrete-Time Fourier Transform Properties → Differences with Continuous-Time, Periodicity, Linearity, Time and Frequency Shifting, Conjugate Summetry, Differencing and Accumulation, Time Reversal and Expansion, Differentation in Frequency, Convolution and Multiplication, Dualities
- Exercises on Continuous-Time Fourier Series → Fourier Series Coefficients Calculation from Signal Equation, Signal Graph
- Exercises on Continuous-Time Fourier Transform → Fourier Transform from Signal Graph and Equation, Output of LTI System
- Exercises on Discrete-Time Fourier Series and Transform → Fourier Series Coefficient, Fourier Transform Calculation and LTI System Output
Filtering, Sampling, Modulation, Interpolation
- Filtering → Convolution Property, Ideal Filters, Series R-C Circuit and Moving Average Filter Approximations
- Continuous-Time Modulation → Getting into Modulation, AM and FM, Demodulation
- Discrete-Time Modulation → Applications, Carriers, Modulation/Demodulation, Time-Division Multiplexing
- Sampling → Sampling Theorem, Sampling, Reconstruction and Aliasing
- Interpolation → Reconstruction Procedure, Interpolation (Band-limited, Zero-order hold, First-order hold)
- Processing Continuous-Time Signals as Discrete-Time Signals → C/D and D/C Conversion, Discrete-Time Processing
- Discrete-Time Sampling → Discrete-Time (or Frequency Domain) Sampling, Downsampling / Decimation, Upsampling
- Exercises on Filtering → Filter Properties, Type and Output
- Exercises on Modulation → CT and DT Modulation Examples
- Exercises on Sampling and Interpolation → Graphical/Visual Sampling and Interpolation Examples
Final words | Next up
And this is actually it for today's post!
Next time we will get into how the Laplace Transform can be used to simplify calculations on Second-Order Systems...
See Ya!

Keep on drifting!

