[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems in order to cover System Representation in Continuous-Time using Differential Equations.
I highly suggest reading the previous article about Discrete-Time, as the representation is quite similar, in some sense.
So, without further ado, let's get straight into it!
Linear Constant-Coefficient Differential Equation
In Continuous-Time, Linear Time-Invariant (LTI) Systems are quite easily representable using linear differential equations with constant-coefficients (LCCDE).
Such equations are of the form:

where each derivative of the system response and input is in Leibniz notation.
Homogeneous Equation
In order to find the solution, let's first set the sum that contains the system response equal to zero.
That way its easy to end up with a homogeneous equation with solution yh:

Due to the nature of those equations, whenever some particular yp(t) satisfies the general equations, there has to exist some yh(t), for which their sum yp(t) + yh(t) satisfies the homogeneous equation.
Notation explained:
- yp(t): Particular solution
- yh(t): Homogeneous solution
Homogeneous Solution
The homogeneous solution has to be of the following exponential form:

Substituting this form in the homogeneous equation results in:

The equation:

has N roots, si, which give us the homogeneous solution:

Auxiliary Conditions
Combining such a homogeneous solution with a particular solution, its possible to calculate the solution of the differential equation.
In other words, the solution will be of the form:

For this to be true, N auxiliary conditions are needed, which are basically the values of the derivatives of the system response y for some initial time t = to:
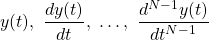
For linear systems the initial conditions are usually 0, whilst for causal LTI systems, at initial rest:

Explicit Recursive Solution
Assuming causality, when given:
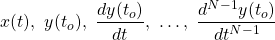
its possible to calculate y(to).
Similarly, this newly calculated value can be used in order to calculate y(to + 1). Thus, this procedure can be continued on indefinitely, and so recursively.
As such, at initial rest, where the rest solution is known from auxiliary solutions, any other solution will be calculated from:

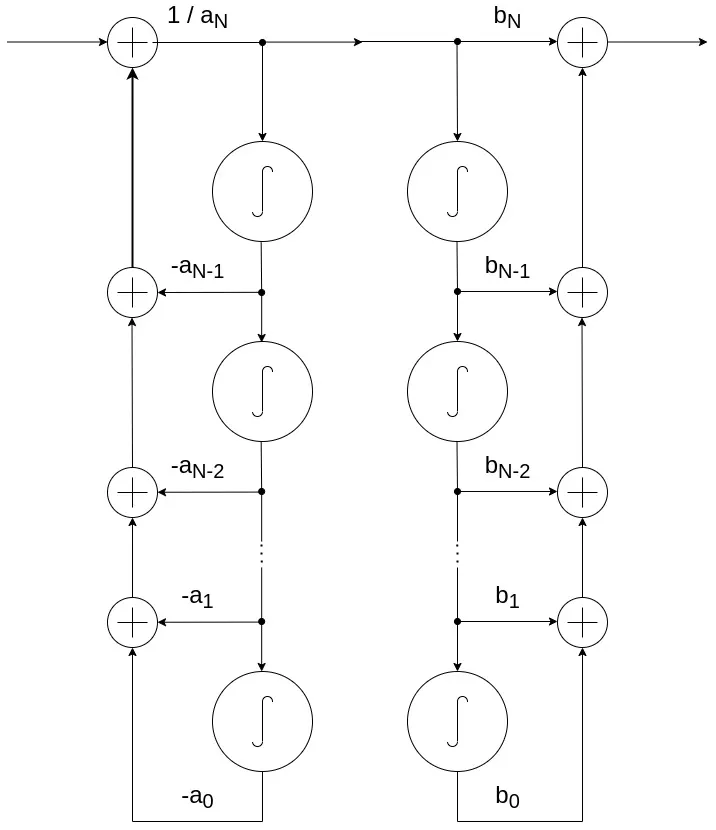
Block Diagram Representation
Replacing the delay with an integrator, the block diagram for continuous-time is basically the same as the block diagram for discrete-time. Integration is visualized using an integration block, whilst the various coefficients are put on top of the connection lines.
Direct Form I Implementation
In Direct Form I, a system in continuous-time can be represented as follows:

The two subsystems, or chains, can also be connected in reverse, resulting into the following representation:
Direct Form II Implementation
Combining the two chains of integrators into one chain, its possible to compact the design even more.
This form is known as the Direct Form II Implementation, and is visualized as follows:

RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io
Previous articles of the series
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
Final words | Next up
And this is actually it for today's post!
See Ya!

Keep on drifting!

