[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems in order to cover Exercises on Continuous-Time Fourier Transform.
So, without further ado, let's get straight into it!
Continuous-Time Fourier Transform Recap
Let's quickly refresh our knowledge on the Fourier Transform. The Fourier Transform is a way of representing signals as a sum of coefficients, but with the coefficients taken as samples of an envelope. The main advantage of using envelopes as the "seed" of the coefficients is that changing the form of the envelope yields a change in the shape of the signal over a period, but independent of the period.
The envelopes, and so the Fourier Transform (analysis) equation, are defined as follows:
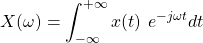
The Inverse Fourier Transform (synthesis) equation, which gives back the original signal is defined as:

The calculation can be skipped for many common signals through the use of tables of Fourier transform pairs.
Fourier Transform from Signal Graph [Based on 8.1 from Ref1]
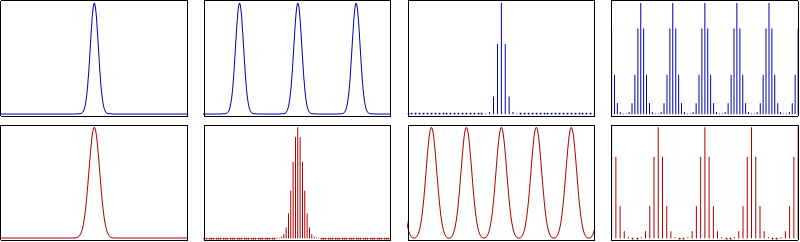
Let's consider signal x(t), which is a single triangular pulse of unit height. The pulse is symmetric about the origin and has a total width of T1.
- Sketch x(t)
- Sketch
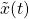 , which is a periodic repetition of x(t) with period To = 3T1 / 2
, which is a periodic repetition of x(t) with period To = 3T1 / 2 - Compute the Fourier Transform of x(t), X(ω). Sketch it for |ω| ≤ 4π / Τ1
- Compute the Fourier Series coefficients of
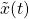 , ak. Sketch for k = 0, ±1, ± 2, ± 3
, ak. Sketch for k = 0, ±1, ± 2, ± 3
Solution
a.
The total width of the signal is T1 and because the signal x(t) is symmetrical it has to be sketched in the range (- T1 / 2, T1 / 2).
Its amplitude will be 1 at the origin, so the graph is as follows:

b.
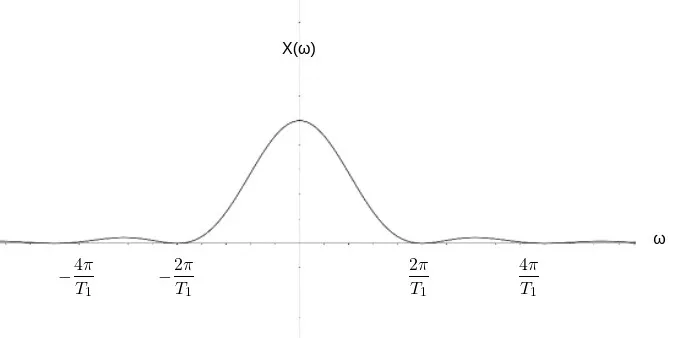
The signal 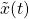 is a repetition of x(t) every To = 3 T1 / 2 time units.
Because the original signal has a width of T1, there will be zero amplitude for a total of T1 / 2 units before and after the signal.
Graphically, we thus have:
is a repetition of x(t) every To = 3 T1 / 2 time units.
Because the original signal has a width of T1, there will be zero amplitude for a total of T1 / 2 units before and after the signal.
Graphically, we thus have:

c.
From the tables, the Fourier Transform of a triangle function, like x(t), is known to be equal to the sinc function squared, or:

Proving this result is quite tedious as integration by parts is needed. A nice proof can be found here
Graphically, the squared sinc function looks like this:
d.
Similar to the Fourier Transform, the Fourier series coefficient is again a squared sinc function, but with a different amplitude.
More specifically, the calculation leads us to:
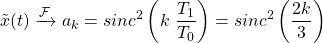
Graphically, the Fourier series is identical to the Fourier transform in all but the magnitude:

Its also easy to notice that the relation between ak and X(ω), which is:

is satisfied completely in the case of this example.
Fourier Transform from Signal Equation [Based on 8.2 from Ref1]
Consider the following signals:
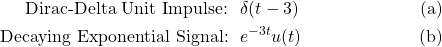
Let's find the Fourier transform of each of those signals.
Solution
a.
The unit impulse function is one of the common signals. From the table that can be found at Ref2, the generic result for δ(t-a) is:

So, in the case of a = 3, the result is the following complex exponential:

b.
The right-sided decaying exponential is also one of the common signal cases, which is defined as:

For a = 3, the result is as follows:

Output of LTI System [Based on 9.7 from Ref1]
The output of a causal LTI system is related to the input x(t) by the following LCCDE:
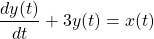
- Determine H(ω) = Y(ω) / X(ω)
- For x(t) = e-tu(t) determine the Fourier Transform of the output, Y(ω)
- Using the Inverse Fourier Transform calculate y(t)
Solution
a.
Let's start by taking the Fourier Transform of the LCCDE.
The signals x(t) and y(t) are simple as they give X(ω) and Y(ω) respectively.
But, in the case of dy(t) / dt, the differentiation property needs to be applied, which as we know yields jωY(ω).
Thus, the final result is:
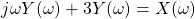
Next, let's take the common term Y(ω):
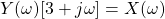
As such, H(ω) is equal to:

b.
The decaying exponential x(t) is one of the common cases, which gives:

Thus, the Fourier Transform of the output is equal to the multiplication of X(ω) and Y(ω):
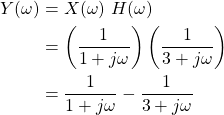
c.
The resulting output Y(ω) is a sum of common signals, which makes taking the inverse Fourier transform of it a piece of cake.
So, the output y(t) is:
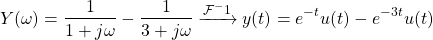
RESOURCES:
References
- Alan Oppenheim. RES.6-007 Signals and Systems. Spring 2011. Massachusetts Institute of Technology: MIT OpenCourseWare, License: Creative Commons BY-NC-SA.
- https://www.thefouriertransform.com/pairs/fourier.php
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io and GeoGebra
Previous articles of the series
Basics
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
LTI Systems and Convolution
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Exercises on LTI System Properties → Superposition, Impulse Response and System Classification Examples
- Exercise on Convolution → Discrete-Time Convolution Example with the help of visualizations
- Exercises on System Representation using Difference Equations → Simple Block Diagram to LCCDE Example, Direct Form I, II and LCCDE Example
- Exercises on System Representation using Differential Equations → Equation to Block Diagram Example, Direct Form I to Equation Example
Fourier Series and Transform
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
- Continuous-Time Fourier Transform Properties → Linearity, Time-Shifting (Translation), Conjugate Symmetry, Time and Frequency Scaling, Duality, Differentiation and Integration, Parseval's Relation, Convolution and Multiplication Properties
- Discrete-Time Fourier Series & Transform → Getting into Discrete-Time, Fourier Series and Transform, Synthesis and Analysis Equations
- Discrete-Time Fourier Transform Properties → Differences with Continuous-Time, Periodicity, Linearity, Time and Frequency Shifting, Conjugate Summetry, Differencing and Accumulation, Time Reversal and Expansion, Differentation in Frequency, Convolution and Multiplication, Dualities
- Exercises on Continuous-Time Fourier Series → Fourier Series Coefficients Calculation from Signal Equation, Signal Graph
Final words | Next up
And this is actually it for today's post!
Next time we will get into exercises on the discrete-time Fourier series and/or transform!
See Ya!

Keep on drifting!

