
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems in order to cover Continuous-Time Fourier Transform Properties.
So, without further ado, let's dive straight into it!
Why the Fourier Transform is so Useful
In the previous two articles we tried to represent continuous-time signals for use in LTI systems. This procedure inevitably took us to sums of basic signals, in the form of complex exponentials, which in turn are known as Fourier Series and can be used to represent periodic signals. Using envelopes as the basis of the sum allowed for the representation of aperiodic signals. These final mathematical equations are known as the Continuous-Time Fourier Transform analysis and synthesis equations, with the later being commonly referred to as the Inverse Fourier Transform.

As such, the Fourier Transform is basically a function that takes in a signal x(t) and turns it into X(ω), commonly denoted as:
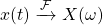
In a similar sense, the Inverse Fourier Transform is a function that takes in X(ω) and gives us the original signal x(t), commonly denoted as:

This "transformation" of x(t) into X(ω), and vice versa, has some very useful properties, that we will cover in the next sections. Of course, all these properties are also satisfied by the Fourier series, but I decided to only cover the Fourier Transform (at least for now).
Linearity
The simplest property comes directly from the analysis equation, as the Fourier Transform is a linear function. This linearity can be expanded to any linear combination of signals.
Mathematicaly, for n weighted signals linearity can be expressed as follows:
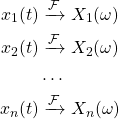
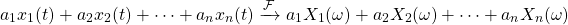
Time-Shifting (or Translation)
Another very useful property is time-shifting. Consider a signal x(t) that gets shifted through time by to, giving the signal x(t - to). As such, its Fourier transform will be phase-shifted, causing a different amplitude. The exact amount of amplitude change is proven to be an complex exponential that's related to to.
Let's skip the proof and get directly into the math:
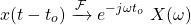
And because visualizations are always easier to understand, here is how the Fourier Transform changes when time-shifting the unit pulse function:

[Image 2]
Conjugate Symmetry
The next property has to do with conjugates of complex numbers.
For time functions with real values (no imaginary part) the Fourier transform satisfies the following property of conjugate symmetry:

This property allows us to easily specify if a given function is real, imaginary or complex.
The real part and magnitude of the Fourier transform of real-valued time functions is an even function of frequency, whilst the imaginary part and phase are odd functions of frequency. In addition to that, because of conjugate symmetry, only positive values of ω are necessary to be calculated for real functions.
Let's get into the mathematical representation of all this.
The Fourier transform X(ω) of any signal x(t) can be represented as a complex number in the following manner:

When x(t) is real then X(-ω) = X*(ω), which results in the real part being even and the imaginary part being odd:

Time and Frequency Scaling
Next up is the time and frequency scaling property of the Fourier Transform.
Scaling a signal x(t) by a factor a, results in a signal x(at), with the following Fourier Transform:

Thus, time-scaling by a results in frequency-scaling by 1 / a.
Its also worth noting that a = -1, which leads to the time-reversal of a signal, also leads to the inversion of the Fourier Transform:

Duality between the Time- and Frequency-Domain
Looking into the analysis and synthesis equations of the Fourier Transform its easy to notice that the equations are quite similar. This "symmetry" between the two equations results in a property known as Duality (**insert Slipknot reference here**).
For example, due to duality, frequency-shifting is of the form:

which is quite similar to the time-shifting equation!
But, where this really gets illustrated better, is in diagrams like the following:
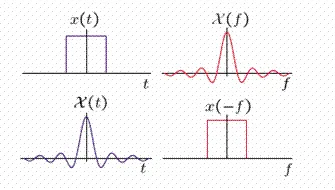
[Image 3]
The Fourier transform of a unit pulse with length To is:

But, its also possible to get a Fourier transform of unit pulse form with length wo as the output.
This is done by using the following signal:

Therefore, whenever one pair of Fourier Transforms is known, another "symmetric" one is also known!
Differentation and Integration
The properties wouldn't be complete if we didn't mention differentation and integration. Of course, the Fourier Transform can be used with differentials and integrals of signals.
Differentiating both sides of the Fourier Transform leads into the following differentiation property:

Similarly, the integration of both sides, leads into the integration property:

which is a little bit more complex.
Parseval's Relation
For any Fourier transform pair x(t) and X(ω) the following relation, known as the Parseval relation, is true:

Something similar is also true for the Fourier series that is used to represent periodic signals:

Convolution and Multiplication
Lastly, let's also cover the convolution and multiplication properties.
Considering an LTI system with input x(t) and impulse response h(t), the Fourier Transform of their convolution, which is the system output y(t), is equal to the multiplication of the individual Fourier Transforms:
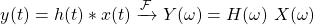
On the other hand, multiplying two signals x(t) and y(t) leads into a so called modulation, which is also why the multiplication of two signals is generally known as (amplitude) modulation.
Mathematically, the Fourier transform of the product of two signals is equal to the convolution of their individual Fourier transforms, multiplied by a factor 1 / 2π:

RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io
Previous articles of the series
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
Final words | Next up
And this is actually it for today's post!
Next time we will get Discrete-Time Fourier Series, which are used to represent Periodic Signals in Discrete-Time!
See Ya!

Keep on drifting!


