
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems in order to cover the Laplace Transform Properties.
So, without further ado, let's get straight into it!
Laplace Transform
In the previous article we covered how we end up with the Laplace Transform, and why it can be used to analyze systems that don't converge using the Fourier Transform. The Laplace Transform is basically a generalization of the Fourier Transform, where the exponent is a complex number. We also mentioned that the Laplace Transform can sometimes simplify the calculations for LTI Systems, and more specifically higher-order systems.
By definition, the Laplace Transform is calculated using:
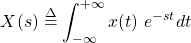
The inverse Laplace Transform is defined as follows:
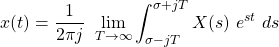
Of course the Laplace Transform has similar properties to the Fourier Transform, which of course include linearity, time- and frequency-shifting, time-scaling, conjugation, differentiation etc. And it's also interesting and neseccary to cover how the ROC is affected when such properties come into play! So, let's get into them...
Laplace Transform Properties
Linearity
Consider the following two Laplace Transforms:

For any linear combination:

the resulting Laplace Transform is given by:

where the ROC is the intersection of the two individual ROCs.
Time- and Frequency-Shifting
Let's consider the Laplace Transform:
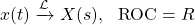
The Laplace Transform of the time-shifted x(t - t0) has the same ROC and is given by:
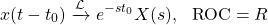
whilst the frequency-shifted es0t x(t) has a different ROC and is given by:

Time-Scaling
Time-scaling a signal by a> yields the following Laplace Transform:

As such time-inversion (multiply by -1) yields an inversion of the ROC:

Complex Conjugation
The complex-conjugate x*(t) has the same ROC as the original signal, and its Laplace Transform is defined as:

When the signal  is real, the result is basically
is real, the result is basically  .
.
Multiplication and Convolution
Similar to the Fourier Transform, Multiplication turns into Convolution, whilst Convolution turns into Multiplication. As such this pair of properties is defined as:

with the ROC at least including the union of the two individual ROCs:
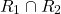
The actual formula for calculating the convolution is a little bit different than what we are used to, but let's not get into it now as it doesn't really matter anyway.
Differentation in Time-Domain
The derivative of a signal has a Laplace Transform that is given by:
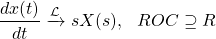
where the resulting ROC contains the original ROC.
Differentation in Frequency-Domain
The derivative in the Frequency-Domain yields the following property:
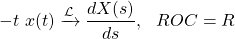
which is quite useful in lots of applications.
Integration in Time-Domain
Integration is more common to be used in the Time-Domain. The Laplace Transform of the integral of signal x(t) is given by:
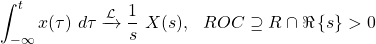
where the ROC includes the previous ROC and the positive values of the real part of s.
Initial and Final Value Theorems
Lastly, there are also two quite important theorems that have to be mentioned.
The initial value theorem is defined as:

where the following conditions have to be met:

and no pulses or high-order anomalies should be in the beginning of x(t).
In addition to this theorem, if  and
and  has a finite limit for
has a finite limit for  , the so called final value theorem defines that:
, the so called final value theorem defines that:

RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io and GeoGebra
Previous articles of the series
Basics
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
LTI Systems and Convolution
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Exercises on LTI System Properties → Superposition, Impulse Response and System Classification Examples
- Exercise on Convolution → Discrete-Time Convolution Example with the help of visualizations
- Exercises on System Representation using Difference Equations → Simple Block Diagram to LCCDE Example, Direct Form I, II and LCCDE Example
- Exercises on System Representation using Differential Equations → Equation to Block Diagram Example, Direct Form I to Equation Example
Fourier Series and Transform
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
- Continuous-Time Fourier Transform Properties → Linearity, Time-Shifting (Translation), Conjugate Symmetry, Time and Frequency Scaling, Duality, Differentiation and Integration, Parseval's Relation, Convolution and Multiplication Properties
- Discrete-Time Fourier Series & Transform → Getting into Discrete-Time, Fourier Series and Transform, Synthesis and Analysis Equations
- Discrete-Time Fourier Transform Properties → Differences with Continuous-Time, Periodicity, Linearity, Time and Frequency Shifting, Conjugate Summetry, Differencing and Accumulation, Time Reversal and Expansion, Differentation in Frequency, Convolution and Multiplication, Dualities
- Exercises on Continuous-Time Fourier Series → Fourier Series Coefficients Calculation from Signal Equation, Signal Graph
- Exercises on Continuous-Time Fourier Transform → Fourier Transform from Signal Graph and Equation, Output of LTI System
- Exercises on Discrete-Time Fourier Series and Transform → Fourier Series Coefficient, Fourier Transform Calculation and LTI System Output
Filtering, Sampling, Modulation, Interpolation
- Filtering → Convolution Property, Ideal Filters, Series R-C Circuit and Moving Average Filter Approximations
- Continuous-Time Modulation → Getting into Modulation, AM and FM, Demodulation
- Discrete-Time Modulation → Applications, Carriers, Modulation/Demodulation, Time-Division Multiplexing
- Sampling → Sampling Theorem, Sampling, Reconstruction and Aliasing
- Interpolation → Reconstruction Procedure, Interpolation (Band-limited, Zero-order hold, First-order hold)
- Processing Continuous-Time Signals as Discrete-Time Signals → C/D and D/C Conversion, Discrete-Time Processing
- Discrete-Time Sampling → Discrete-Time (or Frequency Domain) Sampling, Downsampling / Decimation, Upsampling
- Exercises on Filtering → Filter Properties, Type and Output
- Exercises on Modulation → CT and DT Modulation Examples
- Exercises on Sampling and Interpolation → Graphical/Visual Sampling and Interpolation Examples
Laplace and Z Transforms
- Laplace Transform → Laplace Transform, Region of Convergence (ROC)
Final words | Next up
And this is actually it for today's post!
Next time we will get into how LTI systems can be analyzed using the Laplace Transform...
See Ya!

Keep on drifting!

