
Hello it's a me again drifter1! Today we continue with yet another post about Physics and more specifically some more advanced examples in Newton Laws! This is the last post in the topic of Classical mechanics for now and I hope that you enjoyed the series so far!
To understand the examples I suggest you to read some of my previous (theory) posts like:
And maybe the previous examples in:
So, after this big introduction and suggestion list we can now get started!
Example 1:
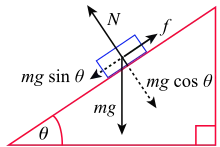
A man is pushing a box (of mass m) with a horizontal force F on top of an inclined plane of θ angle. Supposing that the box is moving with an constant velocity and that there is no friction, calculate the force as a function of m and θ.
Gravity is g = 9.8 m/s^2.
We've done similar examples inprevious posts, but there are some differences now.
Supposing that the angle is: 0 < θ < 90 degrees we analyze the weight into components.
mgcosθ vertically and mgsinθ horizontally.
In the vertical axis we have no motion (1st law) and so N = mgcosθ that would be useful if there was friction, that we don't have in this example.
Using the 1st law on the horizontal axis too (because velocity is constant) we have:
ΣF = 0 =>
F = mgsinθ =>
F = 9.8*msinθ N
m > 0 Kg and 0 < θ < 90 degrees
I know that this was not so special, but having variables is sometimes more difficult to understand! I know a lot of people who struggle with variables, cause defining and describing the problem in equations becomes more difficult.
Example 2:
 (digitizer drawing)
(digitizer drawing)
We have the upper situation, where an object of 10kg is standing on top of an inclined plane of an 30 degree angle. It is tied with another object of m mass using a thread. The pulley has no friction, the kinetic friction factor is 0.35 and the system is initial at rest. Calculate the mass m so that the object of 10kg is moving with an constant velocity on top of the inclined plane.
When having a pulley the force gets passed over using the thread.
That way the total force on top of the 10kg object (1st law) is:
ΣF = 0 =>
T = Wx + Ft (I)
where T is the thread tension, Wx the weight component and Ft the friction.
Analyzing the weight as always we can find that:
Wx = 10gsinθ
and
Ft = μk * N = μk * 10gcosθ (1st law vertically)
The forces applied to the second object are it's weight and the same tension T, because there is no acceleration and that way:
T = mg
From (I) we have:
mg = 10gsinθ + μk * 10gcosθ =>
m = 10sin30 + 0.35 * 10cos30 =>
m ~= 8.03 Kg
Example 3:

A truck is transporting a 20kg box that is first at rest. The friction factors are μs = 0.15 and μk = 0.1. At some stop sign (initial at rest) the truck starts accelerating with an constnat acceleration of 2 m/s^2. We suppose that the truck's door is open and that the box is 2.8m away of it. Will the box fly out of the truck, and if yes how much time passes until the box fells out of the truck?
Gravity is g = 10 m/s^2
Let's first calculate the maximum static friction.
Fs <= μs * N = μs * W = μs*m*g = 30 N
By applying Newton's second law on the truck's motion we get:
F = ma => F = 2m.
This means that a force of F = 2 * 20 = 40 N is applied to the box.
We can clearly see that Fs < F and so the box will start moving and will fly out of the truck.
After sliding the box will have a kinetic friction of:
Fk = μk * N = 0.1*20*10 = 20 N.
This means that the actual force that accelerates it is F - Fk = 20 N and so:
20 = ma => a = 1 m/s^2, where a is the constant acceleration of the box
Because the acceleration is constant we can use the const acceleration equation:
x = x0 + uo*t + a*t^2 =>
2.8 = 0 + 0 + 1 * t^2 =>
t = root (2,8) => t = 1.67 seconds.
Example 4:

A box of 150 kg is being dropped from a plane. The plane is flying at a height of 8,500 m with an velocity of 120 m/s to the ground. A constant horizontal air force of 250N (in the opposite direction of the plane's motion) is applied to the box. Calculate when and where the box will crush to the ground, supposing that t = 0 is the time and x = 0 is the position where it was dropped off the plane.
The initial velocity of the box is equal to the plane's velocity and because the force is applied in the opposite direction the box will start slowing down (and maybe even accelerating later on to that direciton).
Using Newton's 2nd law we have:
F = ma =>
250 = 150 * a =>
a = 5/3 m/s^2
which is the deceleration of the box.
The motion in the vertical axis is a constant acceleration linear motion, where only gravity plays a role. By using the simple equation for such a motion we get:
x = x0 + uo*t + g*t^2 =>
0 = 8,500 + 0 -10*t^2 =>
t^2 = 850 =>
t ~= 29.15 seconds
The position of the box will be:
x = x0 + uo*t + a*t^2 =>
x = 0 + 120*29.15 - 5/3*29.25^2 =>
x ~= 2072 m after the dropping point
Let's check if this makes sense.
Because the deceleration is 5/3 ~= -1.66 m/s^2, let's find the time taken to drop the velocity to zero using the basic equation u = uo + at.
t = u0/a => t = 120 / 1.66 = 72 seconds.
The time taken to hit the ground is less then 72 seconds and so the velocity was in the same direction as the plane and never inversed!
Example 5:

A box of mass m (weight w) is dragged by a force F and moves with a constant velocity on top of a horizontal plane. The force F is directing upwards with an angle θ to the plane. The kinetic friction coefficient is μk.
Calculate:
a) The force F as a function of θ, μk and w
b) Find the angle θ so that the force F needed is the least possible, but the motion is still with constant velocity
a)
Let's analyze the force F into component vectors.
Fx = Fcosθ (horizontally)
and
Fy = Fsinθ (vertically)
Applying Newton's 1st law for each axis we get:
ΣFy = 0 =>
Fy + N = W =>
N = W - Fsinθ (vertically)
ΣFx = 0 =>
Fx = Ft =>
Fcosθ = μk * N =>
Fcosθ = μk * (W - Fsinθ) =>
Fcosθ = μk * W - μk *Fsinθ =>
Fcosθ + μk *Fsinθ = μk * W =>
F (cosθ + μk*sinθ) = μk * W =>
F = (μk * W) / (cosθ + μk*sinθ)
b)
To find the least possible F the denominator must be max, cause μk and W stay the same and only θ changes (division with greater value gives smaller result)
So, we have to find the max of: cosθ + μk*sinθ in the range of 0 < θ < 90
To do so we have to find the first derivative of that function f.
f(θ) = cosθ + μk*sinθ
f'(θ) = -sinθ + μk*cosθ
The points where the derivative gets to 0 are the max/min of that function.
-sinθ + μk*cosθ = 0 =>
μk = sinθ/cosθ = tan(θ) =>
θ = arctan(μk)
So, the best angle has an tangent equal to the kinetic friction coefficient/factor.
Image sources:





And this is actually it!
I hope that the Physics series is interesting enough for you Steemians and that continuing with new branches will get even more people excited about Physics in general! After Classical mechanics we might get into Electromagnetism, but I first want to continue with some Mathematics that I have left out of my blog for quite some time now!
Bye!