
[Custom Thumbnail]
All the Code of the series can be found at the Github repository:
https://github.com/drifter1/compiler
Introduction
Hello it's a me again @drifter1! Today we continue with my Compiler Series, a series where we implement a complete compiler for a simple C-like language by using the C-tools Flex and Bison. In this article we will continue with the implementation of Register Allocation, getting into how we use all the knowledge that was covered in the parts 2-4.Requirements:
Actually you need to read and understand all the topics that I covered in the series as a whole, as these articles will give you access to knowledge about:- What Compiler Design is (mainly the steps)
- For which exact Language the Compiler is build for (Tokens and Grammar)
- How to use Flex and Bison
- How to implement a lexer and parser for the language using those tools
- What the Symbol Table is and how we implement it
- How we combine Flex and Bison together
- How we can pass information from the Lexer to the Parser
- How we define operator priorities, precedencies and associativity
- What Semantic Analysis is (Attributes, SDT etc.)
- How we do the so called "Scope Resolution"
- How we declare types and check the type inter-compatibility for different cases that include function parameters and assignments
- How we check function calls later on using a "Revisit queue", as function declarations mostly happen after functions get used (in our Language)
- Intermediate Code Representations, including AST's
- How we implement an AST (structure and management)
- Action Rules for AST nodes and more
- The target system's architecture and its assembly language (MIPS)
- Register Allocation & Assignment and how we implement it
- How we generate Assembly code for various cases
Difficulty:
Talking about the series in general this series can be rated:- Intermediate to Advanced
- Medium
Actual Tutorial Content
Graph Coloring Register Assignment
Now that we have filled the Adjacency Graph using the Variable Array as help, we can finally get into Register Assignment using Graph Coloring. So, let's now first cover what Graph Coloring is. Afterwards, we will get into a simple greedy (dump) algorithm with which we can solve the problem and the implementation of this greedy Coloring that will return the colors (registers) for our nodes (variables).What is Graph Coloring
Graph Coloring is the problem of assigning colors to certain elements of a graph, following certain constraints. Talking about the most common graph coloring problem which is Vertex Coloring, we are given m colors that we have to "apply" to the vertices, in such a way that two adjacent vertices don't share the same color.As you can see we can quite easily transform the Register Assignment problem into a Graph coloring problem, defining variables as nodes and their colors as registers, which is basically what we did up to this point...
A Greedy Algorithm
For graph coloring problems, we define the so called chromatic number, which tells us the smallest number of colors that are needed to color a specific graph G. Trying to calculate/find such a solution is of polynomial time complexity, because graph coloring is a NP-Complete problem.Instead of finding the most optimal solution, we can use a simple and basic algorithm that just finds a solution. The only limiation of the algorithm is that it can't use more then d+1 colors, where d is the maximum degree of a vertex. So, the worst output of this Greedy algorithm would be using (d+1)-colors.
The steps of this algorithm are:
- Color the first vertex with the first color
- For the remaining vertices:
- Color the currently picked vertex with the lowest numbered color that has not been used in adjacent vertices to it (neighbours).
- When all previously used colors appear on adjacent vertices, then we assign a new color to it.
- Return the color assignments
You can find a Java implementation of this and a more optimal Backtracking algorithm in my article:
Java Graph Coloring Algorithms (Backtracking and Greedy)
greedyColoring() Function
Let's now define a greedy coloring function that returns a colors array, that contains the colors-registers for each node-vertex. The index of each color in the colors array directly corresponds to the index of each variable in the varArray "var-name", that we called g_index. At first all the colors will be "-", which means unassigned.To show us which colors are available for picking, we will define a boolean (integer 0-1) "available" array, that will have its values initialized to 1 before each iteration, making all the colors available.
To start the algorithm we set the color of the first vertex to 0 (colors[0] = 0). After that we simply have to loop through all the remaining vertices, processing the adjacent vertices by flaging the colors of those vertices as unavailable, and coloring the current vertex with the first available color. Lastly, we simply return the color assignment array "colors".
In Code all this can be implemented as:
int *greedyColoring(){
AdjList *l;
int i;
int V = g->vertexCount;
// color array
int *colors;
colors = (int*) malloc(V * sizeof(int));
// initialize all vertices to '-1', which means unassigned
for(i = 0; i < V; i++){
colors[i] = -1;
}
// assign first color (0) to first vertex
colors[0] = 0;
// boolean array that shows us which colors are still available
int *available;
available = (int*) malloc(V * sizeof(int));
// starting off, all colors are available
for(i = 0; i < V; i++){
available[i] = 1;
}
// assign colors to the remaining V-1 vertices
int u;
for (u = 1; u < V; u++) {
// process adjacent vertices and flag their colors as unavailable
l = g->adj[u];
while (l != NULL) {
i = l->index;
if (colors[i] != -1) {
available[colors[i]] = 0;
}
l = l->next;
}
// find the first avaiable color
int cr;
for (cr = 0; cr < V; cr++) {
if (available[cr] == 1){
break;
}
}
// assign the first avaiable color
colors[u] = cr;
// reset values back to true for the next iteration
for(i = 0; i < V; i++){
available[i] = 1;
}
}
return colors;
}generate_statements() Function
And this is it! We are now at the last stand of the Register Allocation-Assignment article! Now, at last we have to define a new function that calls the main_reg_allocation() function on the two AST Trees, creating and managing the varArray and AdjGraph structures. Next, it prints out those structures using their corresponding functions: printVarArray and printGraph, and last but not least it calls the greedyColoring() function. The result array "colors" can then be used to assign registers (reg_name) for the symbol table entries of variables, and also for the temporary variables that we added during the process of Register Allocation.In Code this looks like this:
void generate_statements(FILE *fp){
/* print .text */
fprintf(fp, "\n.text\n");
/* Main Function Register Allocation */
initGraph();
main_reg_allocation(main_decl_tree);
main_reg_allocation(main_func_tree);
printVarArray();
printGraph();
/* Main Function Register Assignment */
int i;
int *colors = greedyColoring();
printf("Colors:\n");
for(i = 0; i < var_count; i++){
printf("%s: %d\n", var_name[i], colors[i]);
}
// assign register-color value as reg_name
list_t *l;
for(i = 0; i < var_count; i++){
l = lookup(var_name[i]);
l->reg_name = colors[i];
}
/* print main: */
fprintf(fp, "main:\n");
}Of course, this function has to be called inside of the main assembly code generation routine "generate_code".
Console Output
At first I should note that I commented out some of the main_reg_allocation() calls in the various cases, as they created unnecessary temporary variables. To see what exactly gets stored into temporary variables I also added some more messages...Running our compiler for the "edited" full_example.c file, and disregarding the parsing-messages, the console output of our compiler now is:
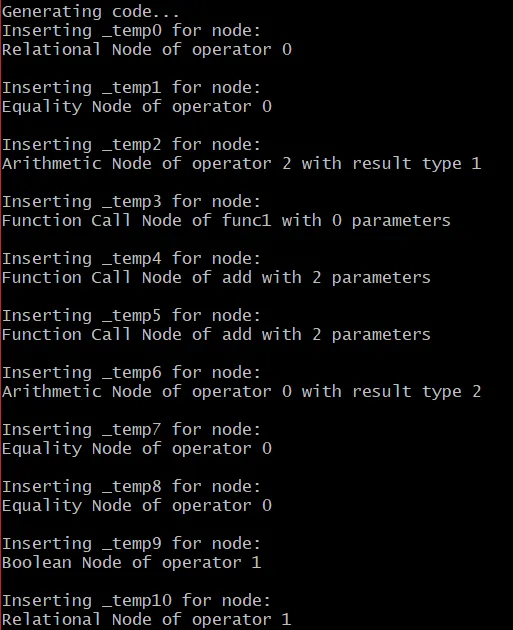
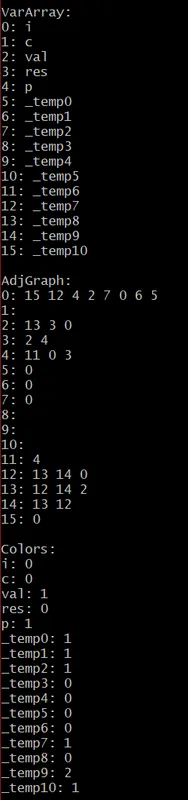
Adding the ".text" and "main:" fprintf() messages, the output file "out.s" now is:
.data
# variables
c: .byte 'c'
i: .word 0
p: .word 0
val: .double 2.500000
res: .double 0.500000, 1.500000, 2.500000, 3.500000, 4.500000, 5.500000
# messages
msg1: .asciiz "\n"
msg2: .asciiz "\n"
msg3: .asciiz "iteration: 3\n"
msg4: .asciiz " "
msg5: .asciiz "\n"
.text
main:
Result Discussion
So, what does the console output tell us? The first part, shows us where exactly the 10 "new" temporary variables get created, so that the various intermediate results can be stored inside of registers. More specifically, we have:
Afterwards we can see the filled-out VarArray and AdjGraph structures and the assigned colors-registers for the variables. I don't think that we have to explain how the graph gets filled or even the graph coloring steps. Just go to GitHub to check out the Code for yourself. Maybe you could run some of the simple examples to understand the procedure better...
RESOURCES
References:
Images:
All of the images are custom-made!Previous parts of the series
General Knowledge and Lexical Analysis
- Introduction
- A simple C Language
- Lexical Analysis using Flex
- Symbol Table (basic structure)
- Using Symbol Table in the Lexer
Syntax Analysis
- Syntax Analysis Theory
- Bison basics
- Creating a grammar for our Language
- Combine Flex and Bison
- Passing information from Lexer to Parser
- Finishing Off The Grammar/Parser (part 1)
- Finishing Off The Grammar/Parser (part 2)
Semantic Analysis (1)
- Semantic Analysis Theory
- Semantics Examples
- Scope Resolution using the Symbol Table
- Type Declaration and Checking
- Function Semantics (part 1)
- Function Semantics (part 2)
Intermediate Code Generation (AST)
- Abstract Syntax Tree Principle
- Abstract Syntax Tree Structure
- Abstract Syntax Tree Management
- Action Rules for Declarations and Initializations
- Action Rules for Expressions
- Action Rules for Assignments and Simple Statements
- Action Rules for If-Else Statements
- Action Rules for Loop Statements and some Fixes
- Action Rules for Function Declarations (part 1)
- Action Rules for Function Declarations (part 2)
- Action Rules for Function Calls
Semantic Analysis (2)
- Datatype attribute for Expressions
- Type Checking for Assignments
- Revisit Queue and Parameter Checking (part 1)
- Revisit Queue and Parameter Checking (part 2)
- Revisit Queue and Parameter Checking (part 3)
- Revisit Queue and Parameter Checking (part 4)
- Revisit Queue and Assignment Checking (part 1)
- Revisit Queue and Assignment Checking (part 2)
- Revisit Queue and Assignment Checking (part 3)
Machine Code Generation
- Machine Code Generation Principles
- MIPS Instruction Set
- Simple Examples in MIPS Assembly
- full_example.c in MIPS Assembly (part 1)
- full_example.c in MIPS Assembly (part 2)
- Generating Code for Declarations and Initializations
- Generating Code for Array Initializations and String Messages
- Register Allocation & Assignment Theory
- Implementing Register Allocation (part 1)
- Implementing Register Allocation (part 2)
- Implementing Register Allocation (part 3)
Final words | Next up on the project
And this is actually it for today's post! I hope that I explained everything as much as I needed to. From next time on we will get into how we generate code for the various statements, starting off with code for the various expressions...Next up on this series, in general, are:
- Machine Code generation (MIPS Assembly)
- Various Optimizations in the Compiler's Code
So, see ya next time!
GitHub Account:
https://github.com/drifter1
Keep on drifting! ;)
