
[Custom Thumbnail]
All the Code of the series can be found at the Github repository:
https://github.com/drifter1/circuitsim
Introduction
Hello it's a me again @drifter1! Today we continue with the Electronic Circuit Simulation series, a tutorial series where we will be implementing a full-on electronic circuit simulator (like SPICE) studying the whole concept and mainly physics behind it! In this article we will talk about Sparse Matrices and how they can be used to optimize our Simulator. The Python Implementation will be discussed in a second part...Requirements:
- Physics and more specifically Electromagnetism Knowledge
- Knowing how to solve Linear Systems using Linear Algebra
- Some understanding of the Programming Language Python
Difficulty:
Talking about the series in general this series can be rated:- Intermediate to Advanced
- Intermediate
Actual Tutorial Content
Sparse Matrix Theory
A sparse matrix (or array) is a matrix in which most of the elements have the value zero. It's the exact opposite of a dense matrix that has mostly nonzero elements. The number of zeros divided by the total number of elements is called Sparsity: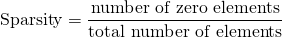
In general a matrix is considered sparse when its sparsity is greater than 0.5.
So, how exactly can we use this concept? Well, storing such matrices and manipulating them on a computer can be done using specialized algorithms and data structures, which take advantage of their sparse nature. Using the standard dense-matrix structures and algorithms we waste processing power and memory on the zeros. Also let's not forget that very large sparse matrices are infeasible to operate with using standard dense-matrix algorithms and structures. Running our simulator for Netlists of millions of components we would never be able to store Matrix A as it would need way too much memory. Even writing the matrix in some file we would still have to loop through billions of entries and lots of zeros which would still take to much time. That's exactly why we only used simple Netlists up to now...
How does a sparse matrix get stored?
Typically a matrix is stored as a two-dimensional array. Each entry of this array represents an element ai, j which we access using the two indices: i (the row index) and j (the column index). Any m×n matrix thereby requires memory proportional to m×n. Talking about sparse matrices, we use other structures (not arrays) that only store the non-zero entries. Such structures save lots of memory, but also make accessing the individual elements more complex. More specifically, the so called formats at which we store spare matrices can be divided into two groups:- Those that allow for efficient modification (e.g. DOK, LIL, COO)
- Those that allow for efficient access and matrix operations (CSC, CSR)
Let's explain how each of them works to see which one will help in our specific optimization...
Dictionary of Keys (DOK)
DOK is a dictionary structure that maps (row, column)-pairs to the value of the elements. Any element that misses from the dictionary is supposed to have the value zero. This format is quite effective for the incremental construction of a sparse matrix in random order, but very bad for iterating over the non-zero values in some order. So, this format is only used for constructing the matrix that later on can be converted to a more efficient format of processing.List of Lists (LIL)
Another great format for constructing a sparse matrix is LIL, which stores one list per row, with each entry containing the column index and value. That way the entries can be looked up much faster as they are sorted by the column index.Coordinate list (COO)
COO stores a list of (row, column, value) tuples. The entries are first sorted by row index and then by column index, to improve the random access times. This makes it another good format of matrix construction.Compressed Sparse Row Format (CSR)
CSR or CRS (compressed row storage) or Yale format represents a sparse matrix using three one-dimensional arrays that contain:- A - nonzero values
- IA - extents of rows
- JA - column indices
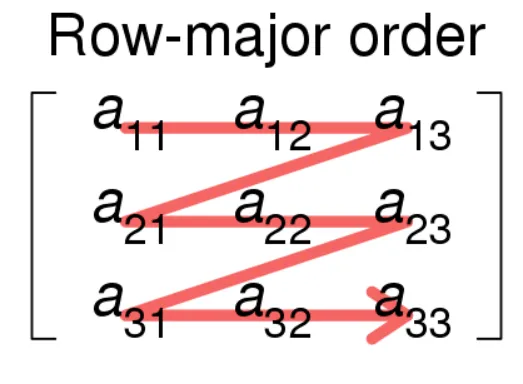
[Image 1]
After looping through the original matrix M, the A array will contain NNZ nonzero entries, whilst the JA array will contain the column index of each of the elements of A, therefore also having a length of NNZ. Supposing that the original matrix M was m × n, the IA array will have a length of m+1. The IA array gets filled recursively as:
IA[0] = 0
IA[i] = IA[i - 1] + (nonzero elements on the (i-1)-th row of M)Wikipedia has the following amazing example:

[Image 2]
Compressed Sparse Column Format (CSC)
Compressing the Columns instead of the Rows in COO, we end up with CSC or CCS (compressed column storage). In this format we read in column-major order: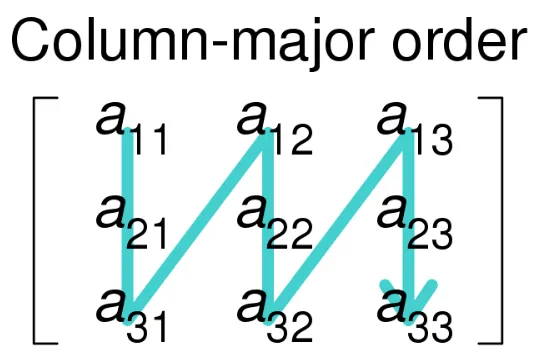
[Image 1]
Looping top-to-bottom and left-to-right we again store in three arrays:
- A - nonzero values
- IA - row indices
- JA - extends of columns
JA[0] = 0
JA[j] = JA[j - 1] + (nonzero elements on the (j-1)-th column of M)The CSC-arrays for the previous example are:
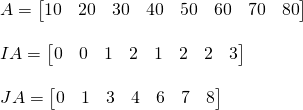
The original matrix had less rows than columns, making CSR more memory efficient (2 less entries) than CSC, but in the case of our simulator we want to turn a square matrix into a sparse matrix, which basically makes both formats equivalent in memory use.
As you might have guessed already, we have to use some of the structures that allows us to access the entries efficiently for matrix operations. (Don't forget that we have to solve a linear system in the end!) CSC is quite efficient for arithmetic operations and matrix-vector products, which makes it perfect for our use-case! The Python Implementation using SciPy will be explained in the second part. I wanted to do an all-in-one article, but we already have way too much information in one article...
RESOURCES
References:
- https://en.wikipedia.org/wiki/Sparse_matrix
Images:

- https://en.wikipedia.org/wiki/Sparse_matrix
Mathematical Equations were made using quicklatex
Previous parts of the series
Introduction and Electromagnetism Background
Mesh and Nodal Analysis
- Mesh Analysis
- Nodal Analysis
- Modified Mesh Analysis by Inspection
- Modified Nodal Analysis by Inspection
Modified Nodal Analysis
- Incidence Matrix and Modified Kirchhoff Laws
- Modified Nodal Analysis (part 1)
- Modified Nodal Analysis (part 2)
Static Analysis
- Static Analysis Implementation (part 1)
- Static Analysis Implementation (part 2)
- Static Analysis Implementation (part 3)
Final words | Next up on the project
And this is actually it for today's post and I hope that you enjoyed it!In the next article, which is basically part 2 of today's article, we will talk about how we use sparse matrices in Python, and also optimize our Static Analysis Simulator... So, see ya next time!
GitHub Account:
https://github.com/drifter1
Keep on drifting! ;)
