[Custom Thumbnail]

All the Code of the series can be found at the Github repository:
https://github.com/drifter1/circuitsim

Introduction

Hello it's a me again @drifter1! Today we continue with the Electric Circuit Simulation series, a tutorial series where we will be implementing a full-on electronic circuit simulator (like SPICE) studying the whole concept and mainly physics behind it! In this article we will modify the Nodal Analysis Method by Inspection, to create the linear system more easily.

Requirements:

Physics and more specifically Electromagnetism Knowledge
Knowing how to solve Linear Systems using Linear Algebra
Some understanding of the Programming Language Python

Difficulty:

Talking about the series in general this series can be rated:

Intermediate to Advanced

Today's topic(s) can be rated:

Intermediate

Actual Tutorial Content

Nodal Analysis Method (Recap)

To recap really quick, Nodal (Node-Voltage) Analysis is based on Kirchhoff's Current Law (KCL), and so calculating the voltage in the various nodes of an electronic circuit (all except one, which is the reference or ground node).

The steps of this method are:

Identify the nodes of the circuit and choose one to be the ground node
Assign labels to each node
Write KCL Equations
Solve the linear system
Solve for other element currents and voltages

Modifying by Inspection

In the 5th article of the series we solved an example "by hand" and using "manual" Python Code explaining each step of the method very in-depth. By the end of this article, during the Python Implementation we found out that the A-matrix contains only Conductances (Inverse of Resistance), whilst the b-matrix contains only Currents, which gave us quite the preview to what we will be analyzing today even further. So, today's topic is actually what exactly comes into each "cell" or coefficient of the linear system.

The example circuit that we solved back then was:

To solve the circuit we basically create the following linear system:

[not so easy to see what we are looking for]

By inspecting the resulting Linear System of this example we see that:

The A-matrix contains only Conductances and:

the diagonal has a positive sign, whilst the rest is negative
each line and row is about a specific node
the diagonal contains the total "self" conductance of each node
the non-diagonal entries contain the mutual conductance between the nodes

The b-matrix contains only Currents and:

each row talks about a specific node
we put a positive sign if the current flows into the node
we put a negative sign if the current flows out of the node

This example contains a voltage source and so creating the linear system automatically "by Inspection" is not that easy! More specifically, I had to apply the method that we will cover next time! In general, Nodal Analysis is suited for electronic circuits with current sources only, whilst Mesh Analysis is more suited for circuits with voltage sources only. This exact problem, will be solved next time, where we will somewhat "combine" the two methods into one. Either way, to generalize for any circuit, let's define some "rules" for the creation of the resistance and voltage matrix, and therefore the whole linear system...

Conductance Matrix

The general form of the Conductance matrix for n-nodes is:

Each entry gets filled based on the following rules:

If the entry is referring to the same node (E.g. G_a,a), we fill it with the total "self" conductance of the corresponding node
If the entry is referring to different nodes (E.g. G_a,b), we fill it with the "negative" mutual conductance of the two nodes

Current Matrix

The general form of the Current matrix for n-nodes is:

Each entry gets filled based on the following rules:

The entry is equal to the sum of all current sources that flow in or out of the corresponding node
The sign of each current in the sum depends on "how" the current flows :

positive sign if the current flows into the node
negative sign if the current flows out of the node

Linear System

So, the general form of the whole linear system is:

Manual Python Implementation

Let's now solve another example that contains only resistances and current sources, by just filling the cells of the linear system's matrices using this new modified method!

Suppose that we have the following circuit:

[Image 1]
(where the upper-left node is called A, whilst the upper-right node is called B)

with the following resistance and current values:

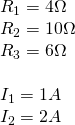
The linear system for this circuit looks like that:

The Python code that solves this problem looks like this:

import numpy as np

'''
Electronic Circuit is
  ┌───┬ R3 ┬───┐
↑ I1  R1   R2  I2 ↓
  └───┴─┬──┴───┘
        ⏚

with following values:
'''
R1 = 4
R2 = 10
R3 = 6
I1 = 1
I2 = 2

'''
Node 0: Connecting I1-R1-R2-I2 (node at the bottom)
Node A: Connecting I1-R1-R3    (upper left node)
Node B: Connecting I2-R2-R3    (upper right node)
'''

# Modified Nodal Analysis By Inspection
a = np.array([[1/R1 + 1/R3, -(1/R3)],[-(1/R3), 1/R2 + 1/R3]])
b = np.array([I1, -I2])
print("A:\n", a, "\n")
print("b:\n", b, "\n")

# Solve System
x = np.linalg.solve(a,b)
print("x:\n", x)

Running this code we get the following:

So, the node voltages are:

RESOURCES

References:

http://www.eeeguide.com/nodal-analysis-examples/
http://mathonweb.com/help/backgd5a.htm

Images:

https://www.swarthmore.edu/NatSci/echeeve1/Ref/mna/MNA1.html

Mathematical Equations were made using quicklatex

Previous parts of the series

Final words | Next up on the project

And this is actually it for today's post! I hope that I was able to explain everything as much as needed!

Next up on this series we will modify Nodal Analysis again to automate the generation of the Linear System for Static (or DC) Analysis. We will basically combine the two methods into one that solves all problems!

So, see ya next time!

GitHub Account:

https://github.com/drifter1

Keep on drifting! ;)

Electronic Circuit Simulation - Modified Nodal Analysis by Inspection [Python]