Hola estimados Steemians de STEM-ESPANOL y comunidad de Steemit en general el día de hoy les comparto un artículo que aborda una de las aplicaciones de las Ecuaciones Diferenciales Ordinarias, es muy común que en nuestras clases los estudiantes pregunten cual es la aplicación del contenido que están estudiando y su utilidad, en este caso es conveniente recordar que las ecuaciones diferenciales se basan en derivadas que expresan matemáticamente la razón a la que una variable cambia respecto a otra.

Fotografía del Cerro Santa Ana tomada desde mi Nokia X2-00 - Elaboración Propia
La rama de la ecología que estudia los cambios que sufren las poblaciones de distintas especies de seres vivos en el tiempo es la dinámica de poblaciones la cual se enfoca en estudiar los cambios en cuanto a número, características, hábitos e interacciones entre las diferentes especies en un mismo hábitat. Uno de los escenarios donde se puede analizar el crecimiento de las poblaciones de animales es en el Cerro Santa Ana ubicado en la Peninsula de Paraguana donde existen diversas especies animales interactuando entre si tales como los conejos de monte y las serpientes, dichas especies se usarán como ejemplo en el presente artículo.
En la naturaleza existen ecosistemas en los cuales la interacción entre dos especies afecta de forma directa a sus poblaciones, en diversas situaciones se podría establecer una relación depredador-presa en este caso las poblaciones de ambas especies pueden ser expresadas mediante un modelo matemático que incluye derivadas de funciones desconocidas por lo cual su expresión matemática se reduce a ecuaciones diferenciales ordinarias, este modelo fue propuesto de forma paralela por Alfred James Lotka y Vito Volterra entre los años 1925 y 1926.
En este punto se puede mencionar como antecedente al modelo depredador-presa que el crecimiento poblacional ya fue estudiado por Thomas Malthus en su obra Ensayo sobre el principio de la población (1798) planteando las denominadas ecuaciones de Malthus sobre el aumento demográfico de las poblaciones en la cual establece que si P(t) es la población en el año t que crece de forma exponencial, la tasa de aumento sería igual a
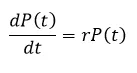
Si bien esta ecuación fue pensada para ser aplicada a poblaciones humanas también puede ser extrapolada al crecimiento demográfico de las poblaciones animales en diversos ecosistemas.
Por ejemplo, en el caso de analizar el escenario donde las serpientes se alimentan de conejos, si x(t) se usa para denotar la población de serpientes en el tiempo t y y(t) a las población de conejos, adicionalmente asumiendo que no hay conejos y que estos representan la fuente de alimento principal de las serpientes al carecer los serpientes de fuente de alimento su población debería decrecer en el tiempo a una tasa (razón de cambio) que es proporcional a la población de serpientes, como la razón de cambio o tasa a la que varía el número de serpientes en el tiempo t puede expresarse como la derivada de x en función de t se cumple que:
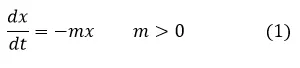
Donde m es una constante que mide el decrecimiento de las serpientes en ausencia de alimento.
Sin embargo, cuando hay conejos en el ecosistema se puede establecer que mientras más conejos o serpientes existan mayor número de interacciones tendrán, es decir, sus interacciones o encuentros son iguales a xy, este hecho permite establecer que el número de serpientes aumenta de forma proporcional al número de encuentros que tengan con su fuente de alimentos, es decir aumentan a razón de nxy, combinando este resultado con la ecuación (1) se obtiene
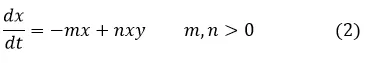
Esta ecuación diferencial ordinaria expresa la razón de cambio (tasa a la que aumenta o disminuye la población) de serpientes en el tiempo en función de las poblaciones de ambas especies existentes, sin embargo, aún debemos analizar como varia la población de los conejos en el tiempo.
En el modelo Depredador-Presa de Lotka-Volterra se asume que la presa tiene una fuente de alimento ilimitado o tan grande que no limita su población (como el pasto) por lo cual su tasa de crecimiento si se asume que no existen depredadores debe ser proporcional al número de individuos de la población (lo cual concuerda con la ley establecida por Malthus), es decir
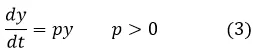
Sin embargo, como las serpientes están presentes la población de conejos disminuye a una tasa proporcional al número de interacciones serpientes-conejos (xy), expresando este hecho de forma matemática se obtiene
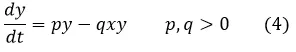
Las ecuaciones diferenciales dos y cuatro constituyen lo que se suele denominar Modelo Depredador-Presa de Lotka-Volterra
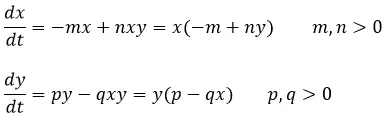
Este sistema de ecuaciones diferenciales es de especial interés debido a que no puede resolverse de forma analítica en términos de funciones elementales por lo cual se suelen usar otro tipo de métodos. Un ejemplo de aplicación de este modelo lo podemos observar en los alrededores al cerro Santa Ana en el cual para el año 2013 según las estimaciones de los habitantes de la zona existía una población de aproximadamente 400 conejos y 400 serpientes, midiendo el tiempo t en semanas y asumiendo unos valores para los parámetros constantes de las poblaciones que se correspondan con la tasa de crecimiento semanal los cuales son aproximadamente de
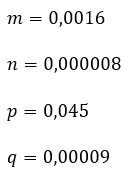
Se establece el siguiente sistema de Ecuaciones Diferenciales Ordinarias

Como este sistema de ecuaciones diferenciales no puede ser resuelto de forma analítica se hará uso de un método numérico para aproximar los valores de la solución.
MÉTODO DE EULER
Más allá de los métodos basados en el análisis matemático utilizados para resolver Ecuaciones Diferenciales Ordinarias los cuales permiten encontrar una solución exacta en los casos en que pueden ser aplicados, también existen una serie de métodos numéricos utilizados para aproximar los valores de la solución.
El lector se preguntara ¿Cuál es la necesidad de utilizar un método numérico si puede obtenerse la solución exacta mediante el cálculo diferencial e integral?, pues bien, en el gran universo de ecuaciones diferenciales ordinarias existentes solo un pequeño número pueden ser resueltas de forma analítica obteniendo la solución exacta, debido a esto han sido desarrollados una serie de métodos numéricos que se utilizan para abordar este tipo de situaciones.
Uno de los métodos más utilizados para resolver este tipo de problemas de forma numérica es el denominado Método de Euler, el cual pertenece a una conocida familia de métodos iterativos que permiten aproximar las soluciones de Ecuaciones Diferenciales Ordinarias sin necesidad de encontrar la solución en términos de funciones elementales.
El método de Euler es uno de los más populares debido a su precisión y a la simplicidad con que es programado, adicionalmente el método solo requiere una condición inicial, la fórmula utilizada en este método es la siguiente:
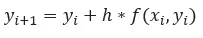
Donde h representa el tamaño del intervalo usado el cual debe tomar un valor pequeño. Basicamente lo que hace este método es estimar el valor de Yi+1 mediante el valor anterior Yi al cual se le suma el tamaño del intervalo h multiplicado por la pendiente f(Xi,Yi) en dicho punto permitiendo de esta forma obtener una aproximación bastante precisa a la solución de la ecuación diferencial ordinaria en el nuevo punto.
En base al modelo planteado anteriormente

Utilizando el Sistema de Álgebra Computacional wxMaxima se puede resolver mediante el siguiente código:
f(x,y):=x * (-0.0016+0.000008 * y)$ / * Ecuación diferencial a resolver * /
g(x,y):=y * (0.045-0.00009 * x)$ / * Ecuación diferencial a resolver * /
x0:400$ y0:400$ / * Condición inicial X0 y Y0 * /
deltax:20$ / * Valor final del intervalo Xn y tamaño de paso * /
fpprintprec:9$ / * Número de cifras decimales */
xn:x0$ n:0$ yn:y0$
while n<=50 do
(
print("",n," ",float(xn)," ",float(yn),"
n:n+1,xn:float(xn+f(xn,yn) * deltax),yn:float(yn+g(xn,yn) * deltax)
);
Generando los siguientes resultados:
| Semana | Serpientes | Conejos |
| 0 | 400.0 | 400.0 |
| 1 | 412.8 | 462.784 |
| 2 | 430.156358 | 520.964536 |
| 3 | 452.246747 | 565.744488 |
| 4 | 478.711828 | 587.423087 |
| 5 | 508.38607 | 578.555978 |
| 6 | 539.178484 | 537.755475 |
| 7 | 568.316162 | 471.628173 |
| 8 | 593.015471 | 392.664483 |
| 9 | 611.295954 | 314.00094 |
| 10 | 622.446084 | 244.794206 |
| 11 | 626.907201 | 188.875141 |
| 12 | 625.79132 | 146.109205 |
| 13 | 620.395417 | 114.445623 |
| 14 | 611.90301 | 91.3933658 |
| 15 | 601.269934 | 74.7336456 |
| 16 | 589.218911 | 62.7318675 |
| 17 | 576.277955 | 54.1187621 |
| 18 | 562.827052 | 47.998542 |
| 19 | 549.138967 | 43.7530643 |
| 20 | 535.410762 | 40.9642715 |
| 21 | 521.786851 | 39.357803 |
| 22 | 508.375493 | 38.7644491 |
| 23 | 495.260581 | 39.0951469 |
| 24 | 482.510208 | 40.3259256 |
| 25 | 470.183109 | 42.4902344 |
| 26 | 458.33376 | 45.6769693 |
| 27 | 447.016727 | 50.0331769 |
| 28 | 436.290698 | 55.7708187 |
| 29 | 426.222562 | 63.1771493 |
| 30 | 416.891845 | 72.6281147 |
| 31 | 408.395797 | 84.6035877 |
| 32 | 400.855411 | 99.701966 |
| 33 | 394.422609 | 118.649258 |
| 34 | 389.288758 | 142.29371 |
| 35 | 385.694452 | 171.570639 |
| 36 | 383.940045 | 207.413104 |
| 37 | 384.395435 | 250.573327 |
| 38 | 387.50586 | 301.311783 |
| 39 | 393.787285 | 358.91744 |
| 40 | 403.800032 | 421.067563 |
| 41 | 418.082766 | 483.154404 |
| 42 | 437.023883 | 537.923343 |
| 43 | 460.652774 | 576.021768 |
| 44 | 488.367249 | 588.083059 |
| 45 | 518.691578 | 568.297098 |
| 46 | 549.256795 | 517.91061 |
| 47 | 577.195125 | 445.946296 |
| 48 | 599.908565 | 365.749358 |
| 49 | 615.818079 | 289.500659 |
| 50 | 624.636659 | 224.552348 |
Evolución de la poblacion de Serpientes y Conejos según el Modelo Depredador-Presa
Se puede observar como la población de ambas especies en un principio tiende a aumentar, sin embargo, cuando hay muchas serpientes la población de conejos empieza a disminuir drásticamente debido a que son cazados, al llegar a un nivel de población muy bajo de conejos las serpientes empiezan a morir debido a no disponer de fuente de alimento y la población de conejos logra recuperarse poco a poco empezando un nuevo ciclo cuando la población de serpientes vuelve a crecer, de esta forma se generan oscilaciones cíclicas en el valor de las poblaciones de ambas especies de animales. La siguiente gráfica permite visualizar los cambios de las poblaciones de ambas especies en el tiempo:
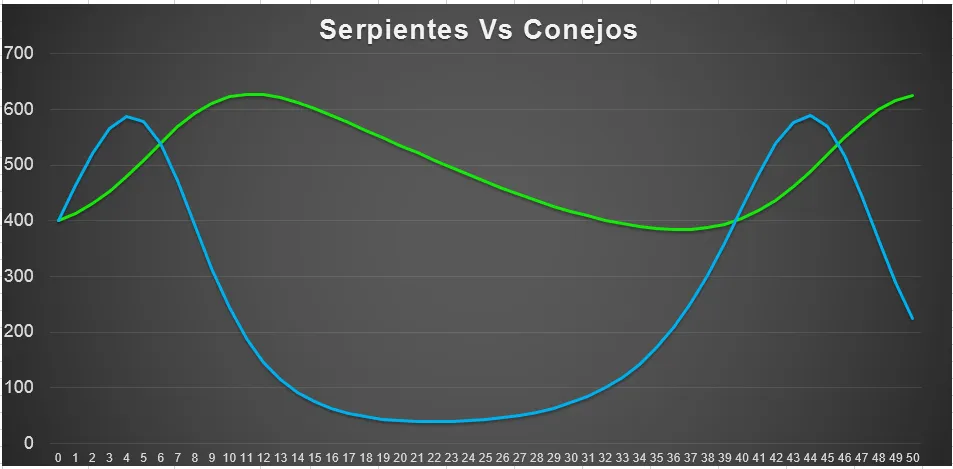
Gráfica de la población de Serpientes (verde) y conejos (azul) en el tiempo
CONCLUSIONES
A pesar de que el modelo Depredador-Presa de Lotka-Volterra no puede ser resuelto de forma exacta, al aplicar el método de Euler se puede resolver de forma numérica obteniendo una solución que en la práctica es suficientemente precisa, la precisión de la solución puede aumentarse al tomar un valor del tamaño de paso h más pequeño.
Los modelos de predicción de la evolución de las poblaciones en sistema Depredador-Presa permiten obtener resultados bastante aproximados a los valores reales, sin embargo, como todo modelo esta sujeto a cierto margen de error porcentual.
REFERENCIAS BIBLIOGRÁFICAS Y MATERIAL CONSULTADO PARA LA ELABORACIÓN DE ESTE ARTÍCULO
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editoria Limusa Willey.
Gámez (1999) Modelo Depredador-Presa Aplicaciones al control biológico, disponible en https://w3.ual.es/~mgamez/articulos/TesisMGC.pdf
Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.
Zill y Cullen (2008) Ecuaciones Diferenciales, 3° Edición, Editorial McGraw-Hill pág. 95-98.
