Saludos estimados lectores de Steemit y miembros de la comunidad científica #stem-espanol y #stemsteem en artículos anteriores he abordado algunas de las aplicaciones de las ecuaciones diferenciales ordinarias en problemas de la vida cotidiana, sin embargo, las ecuaciones diferenciales utilizadas en las ocasiones anteriores han sido todas ecuaciones diferenciales de primer orden, es decir, solo trabajan con derivadas de primer orden (las primeras derivadas de funciones).
Sin embargo, cuando en una ecuación diferencial ordinaria aparecen derivadas de segundo orden (también llamadas segundas derivadas) nos encontramos en presencia de una ecuación diferencial de segundo orden, este tipo de ecuaciones tienen una gran variedad de aplicaciones; en el presente artículo se estudiará su aplicación en el movimiento armónico simple, para lo cual en primer lugar se introducirán algunos conceptos previos.
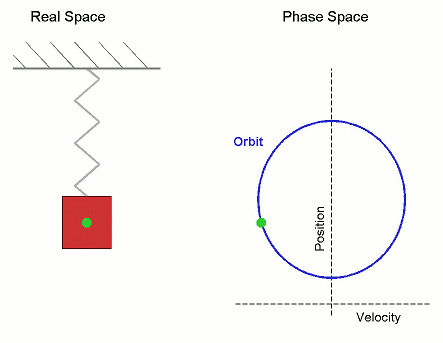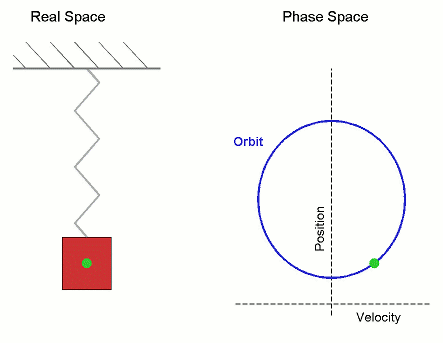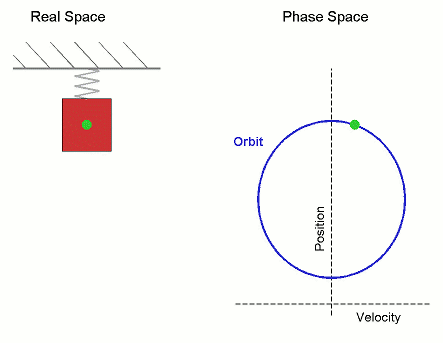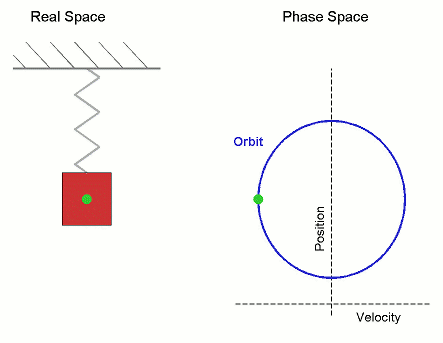
Animación gif sobre el movimiento armónico simple en el espacio real y el espacio fásico, Imagen de Dominio Público. Autor: Mazemaster
Disponible en el siguiente enlace.
Diversos tipos de movimientos pueden ser modelados usando Ecuaciones Diferenciales, por ejemplo el movimiento del péndulo de un reloj sigue un modelo que en física suele denominarse “Movimiento Armónico Simple” este movimiento se basa en oscilaciones periódicas que surgen como resultado de la interacción de dos fuerzas opuestas, según Resnick, Halliday y Krane (1993) el Movimiento Armónico Simple consiste en
Una superposición de oscilaciones armónicas, las cuales pueden describirse en términos de funciones seno y coseno.
Claros ejemplos de este movimiento lo representan la oscilación de un péndulo simple, la vibración de un resorte, entre otros. En este sentido la vibración de un resorte que actúa sobre un cuerpo que se desliza ya sea horizontalmente (en una superficie que no tenga fricción) o verticalmente puede describirse como un Movimiento Armónico Simple. En relación a este tipo de movimiento el físico inglés Robert Hooke (1635-1703) estableció una ley que en la actualidad se conoce como la Ley de Elasticidad de Hooke la cual plantea que:
Si un resorte se estira (o se comprime) L unidades respecto de su posición natural, entonces el resorte arrastra hacia si mismo (o empuja) con una fuerza de magnitud
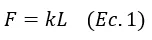
Donde k es una constante positiva, denominada constante del resorte, la cual se mide en unidades de fuerza por unidades de longitud y depende de factores tales como el grosor del resorte y su composición.

Resorte en posición de equilibrio. Imagen elaborada por @ydavgonzalez utilizando el editor de imágenes GIMP
La fuerza ejercida por el resorte se denomina fuerza restauradora. Sin embargo, como se mencionó anteriormente la dinámica del Movimiento Armónico Simple está regida por dos fuerzas que se contrarrestan entre si produciendo este movimiento, en el caso de un resorte suspendido horizontalmente al cual está atado un bloque de masa M las dos fuerzas que interactúan entre ellas son las Fuerza Restauradora y el Peso del objeto, tomando como referencia la definición de Peso que plantean Anton, Bivens y Davis (2010)
La fuerza gravitacional ejercida por la tierra sobre un objeto se llama peso del objeto (o en un sentido más estricto, peso terrestre), de la segunda ley del movimiento de Newton se sigue que un objeto con masa M tiene un peso w de magnitud Mg donde g es la aceleración debida a la gravedad.
Sin embargo, en el ejemplo analizado en este artículo se toma como referencia para la dirección positiva el movimiento hacia arriba del resorte, en este sentido la fuerza de la gravedad terrestre está en dirección negativa (hacia abajo), lo cual se expresa como:
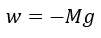
Es importante destacar que este modelo matemático ignora la resistencia del aire y las fuerzas de fricción internas del resorte, de esta forma se analiza el movimiento desde la perspectiva de las dos fuerzas principales involucradas, el peso y la fuerza restauradora.
Para establecer el modelo matemático apropiado se debe determinar una función que permita obtener la posición del objeto y(t) en función del tiempo t, por el momento solo tenemos expresiones para calcular las fuerzas involucradas, razón por la cual en primer lugar se determinará la fuerza total resultante F(t) que actúa sobre el objeto, la cual es igual a la suma de la fuerza restauradora Fr(t) y el peso w (negativo)
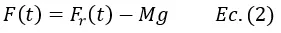
Teniendo en cuenta la segunda ley de newton se puede expresar la fuerza total resultante como el producto de la masa del objeto por la aceleración con la que se mueve, lo cual al sustituir se obtiene
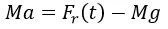
Recordando que sí y(t) expresa la posición de una partícula en función del tiempo, entonces la primera derivada de y(t) representa la velocidad de dicha partícula y la segunda derivada de y(t) representa la aceleración en un instante de tiempo t, se puede sustituir la aceleración por y’’(t) obteniendo
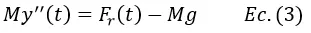
Ahora, al estudiar las fuerzas que actúan sobre el resorte cuando este se encuentra en reposo (aceleración igual a cero), se puede apreciar que se cumple la expresión
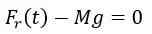
En el momento en que el resorte esta reposo el objeto de masa M se encuentra en el denominado punto de equilibrio (E), al sustituir el valor de la fuerza resultante total (Fr) por el establecido mediante la Ley de elasticidad de Hooke para el punto de equilibrio se obtiene
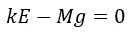
Que equivale a
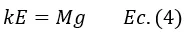
Donde E es el punto en el cual el resorte está en equilibrio, cuando el resorte se estira hasta el punto y(t) entonces se puede decir que se ha desplazado el extremo del resorte E-y(t) por lo tanto aplicando la ley de Hooke la fuerza restauradora en dicho punto será igual a:
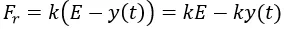
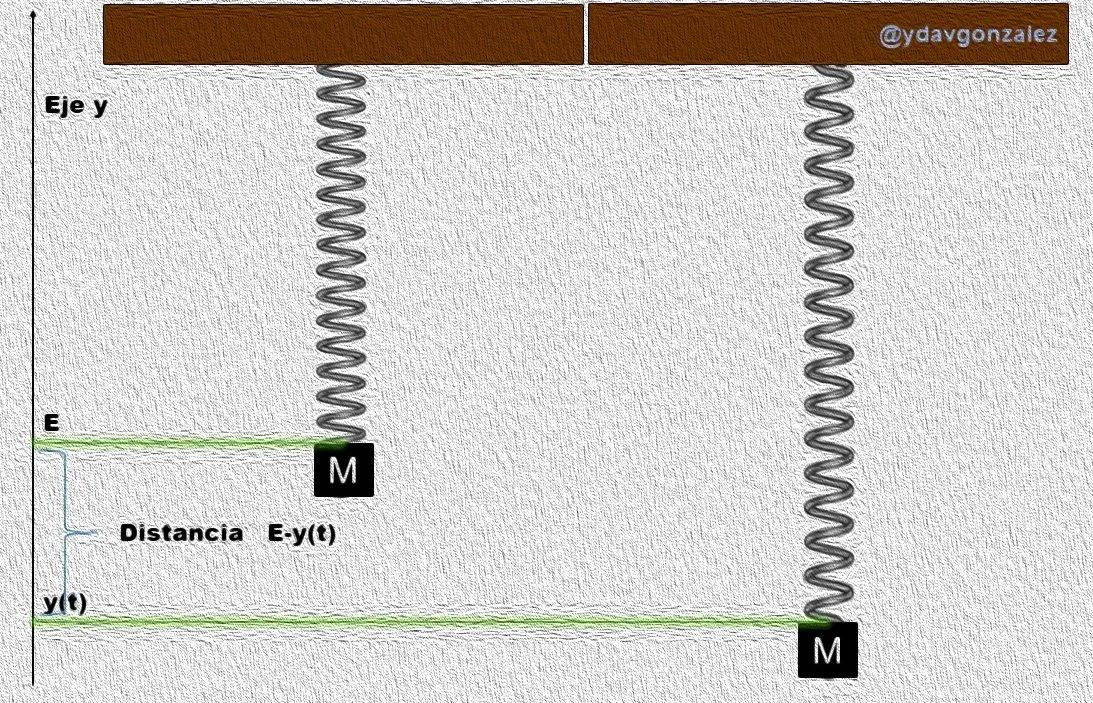
Movimiento del resorte en vibración. Imagen elaborada por @ydavgonzalez utilizando el editor de imágenes GIMP.
Sustituyendo la ecuación número 4 en la fórmula anterior
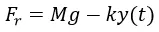
Esta expresión permite calcular la fuerza restauradora que actúa sobre el resorte en función del tiempo t, al sustituir esta fórmula en la ecuación para la Fuerza total resultante se obtiene
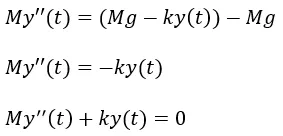
Al dividir entre la masa M resulta
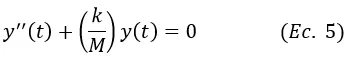
La cual es una Ecuación Diferencial Ordinaria de segundo orden Homogénea con Coeficientes Constantes, que expresa el desplazamiento del resorte en función del tiempo y cuyo método de solución se discute a continuación.
Ecuaciones Diferenciales Ordinarias de Segundo Orden Homogéneas con Coeficientes Constantes
En el cálculo diferencial e integral se denomina ecuación diferencial ordinaria de segundo orden a una ecuación diferencial de la forma general:
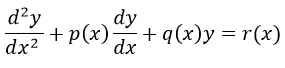
O expresado en notación de y primas
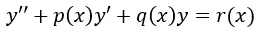
Donde p(x), q(x) y r(x) son funciones solo de x, el término segundo orden hace referencia al hecho de que la derivada de mayor orden que aparece en la ecuación es una segunda derivada, existe una amplia teoría que estudia estas ecuaciones, sin embargo, el caso más elemental ocurre cuando r(x) es igual a cero y los coeficientes p(x) y q(x) toman valores constantes, es decir, una ecuación diferencial de la forma
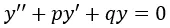
Se denomina Ecuación Diferencial Ordinaria de Segundo Orden Homogénea con Coeficientes Constantes, el método para resolver dicha ecuación es relativamente sencillo.
Paso1: Se encuentra la ecuación auxiliar (ecuación polinómica de segundo grado), la cual se representa como
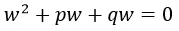
Donde w es la incógnita a calcular, esta ecuación se resuelve obteniendo dos valores de w.
Paso 2: En función de los valores de w obtenidos se establece la solución general de la ecuación diferencial según se muestra en la siguiente tabla:

Tabla N° 1: Solución general de la Ecuación Diferencial Ordinaria de segundo orden homogénea con coeficientes constantes. Fuente: Elaboración propia.
Se puede apreciar que la solución general se muestra como la combinación lineal de dos soluciones linealmente independientes por lo tanto posee dos constantes de integración c1 y c2 cuyos valores pueden determinarse mediante el análisis de las condiciones iniciales del problema.
En algunos casos la solución puede incluir números complejos (Para una introducción a los números complejos pueden leer este artículo de @vjap55). Ahora se determinará la solución a la ecuación diferencial que rige la vibración de un resorte en movimiento armónico simple según se dedujo en la sección anterior
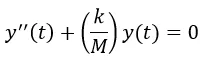
La ecuación auxiliar asociada sería
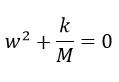
Que al resolver
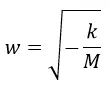
Como el valor de la constante del resorte k es siempre positivo al igual que la masa, el término dentro de la raíz será negativo y la raíz cuadrada será un número imaginario razón por la cual estamos en el tercer caso en el cual
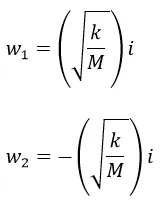
La solución general correspondiente según la fórmula
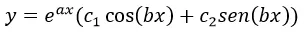
Donde
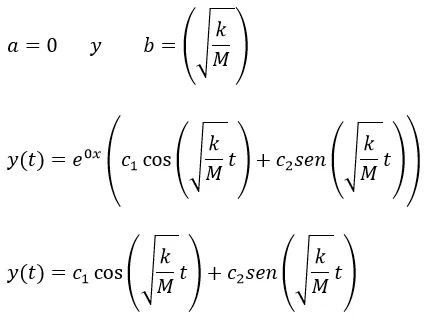
Esta expresión permite determinar la posición del resorte en cualquier instante de tiempo t, para calcular el valor de las constantes presentes se asume que el resorte se suelta desde el reposo en el instante de tiempo 0, entonces se cumple que su posición inicial es y0 y su velocidad (y') es 0 debido a que esta en reposo.

Sustituyendo la primera condición inicial en la solución general
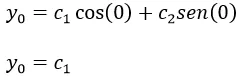
Para sustituir la segunda condición inicial calculamos la derivada de y
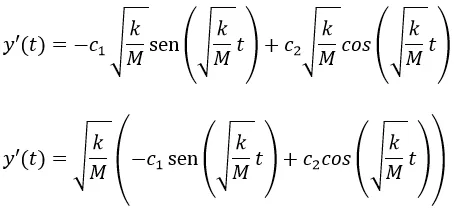
Al sustituir
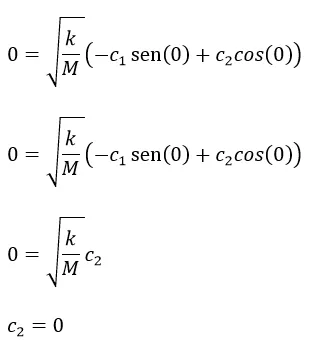
Sustituyendo los valores de C1 y C2 en la solución general resulta
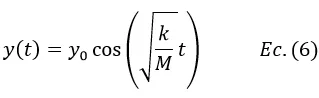
De esta forma se ha obtenido una expresión que permite calcular la posición de un resorte que se suelta desde el reposo en el tiempo t en función de la constante del resorte, la masa del objeto sujetado al extremo y el tiempo.
Como el valor de la función coseno oscila entre 1 y -1 entonces el resorte se desplaza desde y0 hasta –y0, es decir, y0 unidades arriba y abajo del punto de equilibrio E describiendo un movimiento armónico simple de amplitud a=|y0|.
Por otra parte, como el valor del argumento de la función coseno varia de 0 a 2π radianes y luego se repite de forma cíclica el período de la oscilación viene dado por
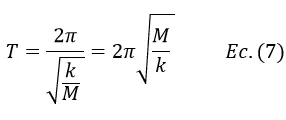
La frecuencia de la oscilación es igual a
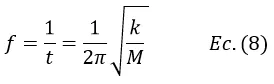
Con estas expresiones se puede determinar la posición del objeto en el extremo del resorte, el periodo de la oscilación y su frecuencia.
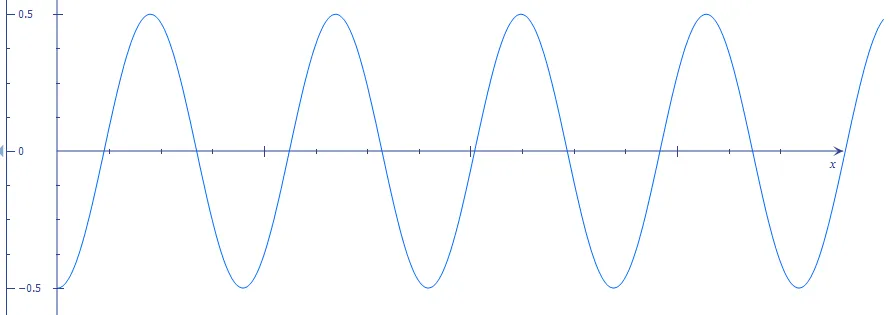
Movimiento del resorte en vibración en función del tiempo (se puede apreciar la oscilación de forma cíclica). Imagen elaborada por @ydavgonzalez utilizando el programa Matemáticas de Microsoft.
Ejemplo:
Suponga que un bloque se encuentra estirando un resorte 0,8 m para alcanzar el estado de equilibrio, suponga asimismo que el bloque se estira 5 m hacia abajo de su posición de equilibrio y que se suelta en el instante de tiempo t=0. Encuentre la función de posición del bloque, la amplitud, frecuencia y período del movimiento de oscilación.
Aunque no se tiene la masa del bloque ni la constante de elasticidad de Hooke se puede determinar el valor del cociente k/M teniendo en cuenta que según la ecuación número 4 obtenida anteriormente
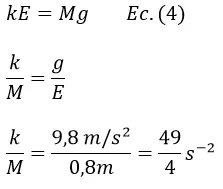
Para determinar la función de posición del bloque se sustituye el valor encontrado en la ecuación número 6
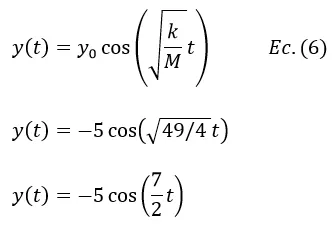
Por razones de simplicidad se omiten las unidades de las magnitudes teniendo en cuenta que para la función posición la unidad correspondiente sería el metro. La amplitud de la vibración es igual
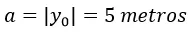
El período se calcula mediante la ecuación número 7
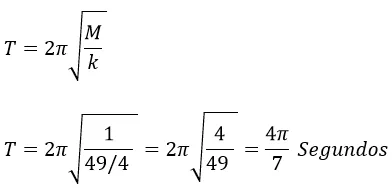
La frecuencia se calcula mediante el siguiente procedimiento
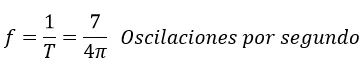
Como se puede apreciar en base a la solución de la ecuación diferencial ordinaria de segundo orden se puede estudiar el movimiento del resorte en vibración mientras describe un movimiento armónico simple.
Conclusiones
En base a los resultados obtenidos en el estudio del movimiento armónico simple y la vibración de un resorte modelada tomando como base la ley de elasticidad de Hooke se pueden establecer las siguientes conclusiones:
- Las ecuaciones diferenciales ordinarias tienen una gran variedad de aplicaciones para resolver modelos matemáticos que representan problemas físicos.
- Para poder considerar la vibración de un resorte como un movimiento armónico simple se deben ignorar las fuerzas de fricción involucradas.
- La resolución de una ecuación diferencial ordinaria de segundo orden implica resolver una ecuación polinómica de segundo grado que puede tener raíces complejas.
- En el artículo se puede evidenciar como usando la segunda ley de Newton y la ley de elasticidad de Hooke se logra modelar la vibración de un resorte con expresiones matemáticas sencillas.
- Los modelos matemáticos basados en las leyes del Movimiento Armónico Simple describen una gran variedad de movimientos presentes en la naturaleza, más allá de la vibración de un resorte.
Espero que este artículo les haya sido útil, recuerden que las matemáticas pueden ser aplicadas a diversos fenómenos físicos lo cual nos permite tener una mayor comprensión de las leyes que rigen nuestro universo, saludos y es un placer ser miembro de la comunidad científica de #stem-espanol y #steemstem.
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editoria Limusa Willey.
González (2018), Aplicación de las Ecuaciones Diferenciales Ordinarias en la Datación de Fósiles mediante el Isótopo Radiactivo Carbono-14 y su resolución mediante el Método de Runge-Kutta de 4° orden. Disponible en el siguiente enlace.
González (2018), Modelado matemático mediante ecuaciones diferenciales ordinarias aplicado al estudio de la dinámica de poblaciones de un sistema depredador-presa (especies presentes en el cerro Santa Ana). Disponible en el siguiente enlace.
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.
Zill y Cullen (2008) Ecuaciones Diferenciales, 3° Edición, Editorial McGraw-Hill pág. 95-98.

Imagen de Dominio Público. Elaborada por @carloserp-2000 y @iamphysical.
