Cuando revisamos las cifras de contagios por COVID-19 podemos inferir que han disminuido en los países que tienen más del 80% de su población objetivo vacunada, y en los que no cuentan con vacunas a nivel nacional las cifras podrían seguir oscilando hasta con tendencia alcista. Se puede dar el caso que tengamos unas gráficas con pendiente negativa (a la baja) y que se pueda dar una correlación lineal entre el número de contagiados y el porcentaje de personas vacunadas, el primer caso mencionado antes, pero cuando existe una dispersión amplia de datos es poco probable que se pueda interpretar como una tendencia hacia arriba o hacia abajo y mucho menos proponer una correlación entre los parámetros señalados.

Este será mi tema a analizar en este artículo, Modelos y ajuste de datos experimentales, que busca analizar la tendencia de un variable dependiente de un parámetro que se considera de referencia.

En algunas ocasiones es muy común escuchar "no tienen ninguna relación", como por ejemplo cuando se hace la gráfica de la altura de 30 niños del salón de clases y la longitud promedio del cabello de cada uno de ellos. Una niña puede medir 1,20 metros de estatura y su cabello extremadamente largo de unos 50 centímetros de largo, mientras que otra chica de esa misma altura puede tener un cabello corto de unos 27 cm y tal vez un niño de esa altura puede tener su cabello al ras de su cabeza con 3 milímetros y su compañero lo tendría de unos 5 cm de largo, en fin no está definida una tendencia de los datos experimentales, que nos pueda encaminar a proponer una conclusión entre estos 2 parámetros, no existiendo una correlación entre ellos.

Correlación:

La dispersión de los puntos experimentales, la data de estatura de los niños y la longitud del cabello, es muy notable, es decir están separados uno del otro, por lo que para una misma estatura podemos tener hasta 6 valores diferentes de la variable "largo del cabello", no existiendo proporcionalidad entre los 2 parámetros.

A manera de ejemplo, podemos realizar un ajuste lineal sobre todos esos pares de puntos ordenados para demostrar visualmente la enorme dispersión que se tiene entre estas 2 variables:

Modelo y ajuste de datos

En un país tan deprimido económicamente como Venezuela, la recesión ha impactado negativamente las actividades de las empresas de producción de insumos automotriz que en el siguiente ejemplo analizaremos el decrecimiento de las fábricas de válvulas para motores durante los últimos 18 años, de manera sostenida y vertiginosa. Veamos si existe una tendencia y si podemos encontrar alguna correlación en este fenómeno que impacta la economía de un país.

La tendencia es a disminuir el número de empresas fabricantes de válvulas para automóviles al transcurrir los años, por lo que existe una correlación de datos en forma negativa. Cuando realizamos un ajuste lineal para determinar la relación de dependencia entre estas 2 variables resulta lo siguiente:

El "valor inicial" dado por la intersección con el eje Y es 20,2 ± 0,9, la tasa de desaparición de empresas viene dada por la pendiente, 1,08 ± 0,09, mientras que la desviación estándar es de 1,5. Es importante destacar que la tendencia no es muy pronunciada y existe una pequeña, pero notable, dispersión de los datos y de allí ese valor de 1,5. También es notorio observar que el método de ajuste a los datos se realiza por mínimos cuadrados, a detallar en la siguiente publicación y que consiste en trazar una línea recta que pase por la mayor cantidad de datos experimentales, además se establece en lo posible discriminar la misma cantidad de puntos sobre (4) la línea recta al igual que los datos que quedan por debajo (4) de ese ajuste.

¿Qué sucede si en vez de hacer un ajuste de regresión lineal aplicamos un modelo de polinomios o exponencial?

Observamos que no hay un cambio significativo con relación al ajuste lineal. además que el segundo coeficiente (C) de la expresión polinómica de orden 2 es 0,005 con un error de ± 0,02. A pesar que tanto el ajuste lineal como el polinomial tienen la misma desviación estándar, el coeficiente de determinación del ajuste R² es mayor en la regresión lineal R² = 0,9671 que en la polinómica R² = 0,9359. Esto da cuenta de la efectividad del ajuste a los datos experimentales en cuanto a los valores de la variable "número de fábricas de válvulas para vehículos" a partir de la variable independiente "años (2003 al 2021)".

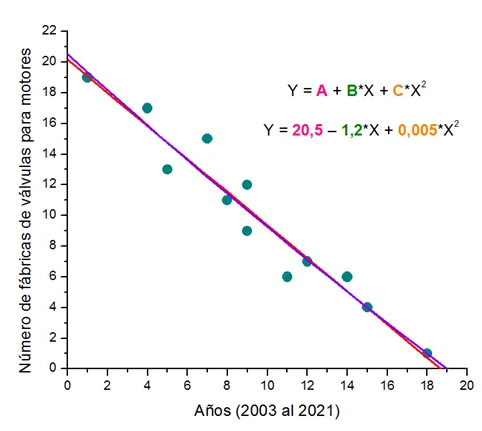
Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en esta publicación pueden ampliarse si consultas las referencias:

• Imagen de geralt: Portada para "dispersión de datos"
• Blog: Ajuste de datos mediante curvas
• Guía: Mínimos cuadrados
• Nota: Gráfico de dispersión en R
• Nota: Diagrama de dispersión

Las funciones matemáticas son expresiones que relacionan
las variables de una igualdad,
así que invariablemente encontraremos alguna solución