Patrones numéricos — Triángulo de Blaise Pascal
Triángulo de Tartaglia o Triángulo Numérico
Si bien es cierto que las pirámides constituyen un enigma de la cultura y civilización ancestral, los lados que la conforman pueden ser tratadas como triángulos dispuestos de manera inclinada respecto a la vertical, por lo que en esta publicación veremos una distribución numérica que tiene una disposición triangular sin ni siquiera tratarse de una figura geométrica sino de una herramienta matemática conocida como el Triángulo de Pascal, aplicado en el Cálculo de Números Combinatorios y Teoría de Probabilidades.
Triángulo de Pascal
Al inicio de nuestra civilización existió la necesidad de ir ordenando las eventualidades que se regían por un patrón, es así como se establecieron los distintos calendarios para ajustarse a las variaciones diarias entre cada día de luz y cada noche de oscuridad. A pesar que antes del año 1654 ya era conocido y aplicado en distintos países lo que se conoce como el Triángulo Aritmético de Blaise Pascal, no es sino después de esta fecha que se estableció una disposición en forma de triángulo que sigue un patrón numérico que puede ser aplicado en Probabilidad, Combinaciones, Polinomios y hasta en la Secuencia de Fibonacci.
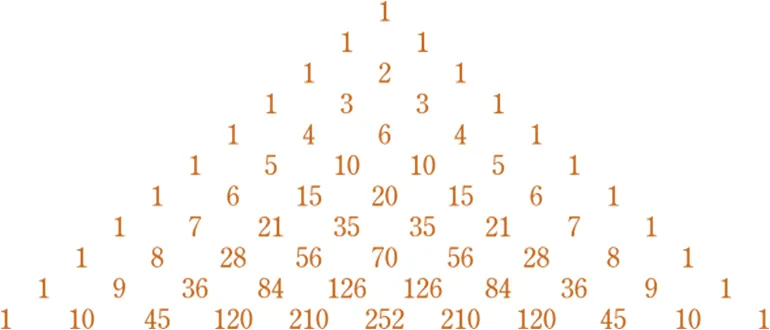
Representación gráfica del Triángulo de Pascal para un número limitado a 10 eventos con el exponente n = 10. Autor: Kazukiokumura
Puede verse como una expansión binomial de la forma (a + b)n, donde los coeficientes del polinomio resultan ser los elementos que conforman cada fila del Triángulo de Pascal.
Por tanto, la construcción de esta distribución numérica para n = 2, sería:
(a + 1)2 = 1 a2 + 2 a + 1
que corresponde con la fila: 1 2 1
mientras que si n= 3, se tiene:(a + 1)3 = 1 a3 + 3 a2 + 3 a + 1
que corresponde con la fila: 1 3 3 1mientras que si n= 3, se tiene:

Combinatoria Triángulo de Pascal
Si utilizamos inteligentemente este tipo de configuración numérica podemos determinar el número de formas distintas en que se pueden combinar cierto número de elementos (k) de un conjunto (n).


Cálculo combinatorio de una selección de 3 círculos de diferentes colores. Autor: @ycam
De acuerdo al cálculo de combinaciones, existen 10 formas diferentes de elegir 3 círculos de distintos colores entre un conjunto de 5: verde, morado, rojo, naranja y azul.
Probabilidad Triángulo de Pascal
Este patrón numérico se emplea en muchos problemas de Probabilidades para eventos que tienen sólo 2 opciones de ocurrencia, como por ejemplo, si tenemos una botella de agua y la lanzamos al aire, ¿cuál es la probabilidad de que la botella caiga parada al menos una vez?

Correspondencia de la Probabilidad de que una botella de agua lanzada al aire caiga parada (p).
Innumerable pueden ser las distribuciones y patrones dentro del Triángulo de Pascal, que se ha ampliado y masificado su utilización en diversas áreas de las ciencias Física, Matemáticas e Ingeniería.
Material bibliográfico recomendado:
(1) Combinaciones. AAA Math
(2) Estadística para todos. El triángulo de Pascal o Tartaglia
(3) Historia y aplicaciones. Pascal Triangle
(4) Triángulo de Pascal. Artículo en Wikipedia
Visita mi BLOG para ver temas interesantes sobre Matemáticas e Ingeniería

