
Fracciones equivalentes
Amplificación y simplificación de fracciones Matemáticas sin secretos: Es una forma de presentar los ejemplos y ejercicios matemáticos de forma amena y sencilla, de tal manera que la etimología y la exposición de cualquier tema no se convierta en un trauma para el aprendiz de las Ciencias Matemáticas y aminorando los procedimientos engorrosos que muchas veces nos encontramos durante el proceso de enseñanza-aprendizaje. Veamos en este artículo una explicación de las fracciones equivalentes, como aquellas que pueden representarse por números fraccionarios distintos, pero que expresan el mismo resultado o fracción.Fracciones
División:Otra manera de distinguir los números fraccionarios es a través de la representación matemática de la división no es más que la fracción o parte de un todo o conjunto total, así que si tenemos un total de 50 manzanas y queremos repartirlas entre 5 personas, deseamos saber ¿cuántas manzanas le tocarían a cada persona?
La respuesta inmediata es 10 manzanas para cada persona. Sin embargo, cuando queremos representar esta repartición como un número fraccionario, recurrimos al formato gráfico:

Amplificación de fracciones
Cuando tengamos un número fraccionario podemos obtener otra fracción equivalentes al multiplicar tanto el numerador como el denominador por una misma cantidad. Esta operación de "multiplicar" se le denomina amplificación de fracciones. Veamos el siguiente ejemplo:


Simple y sencillo, multiplicamos la fracción original por 2 y obtenemos una fracción equivalente:
Podemos "fraccionar" la unidad en tantas "partes" como queramos hacerlo, siempre que consideremos la multiplicación por el mismo número entero, tanto en el denominador como el numerador.
Simplificación de fracciones
En el caso de un número fraccionario cualquiera, se procede obtener otra fracción equivalentes al dividir, tanto el numerador como el denominador por una misma cantidad. Esta operación de "dividir" se le conoce como simplificación de fracciones. Note que es un procedimiento similar al de amplificación de fracciones, pero mejor veamos el siguiente ejemplo:
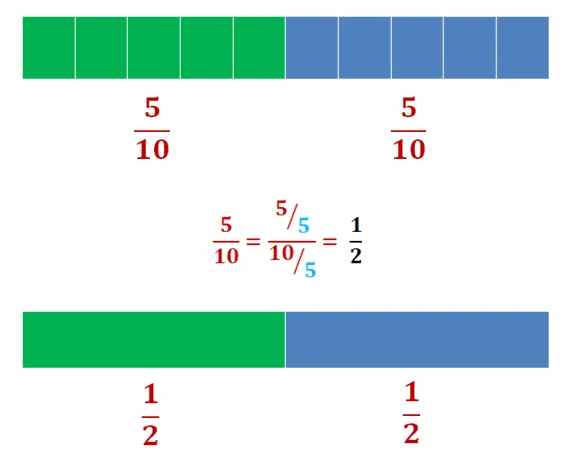
Las fracciones equivalentes pueden facilitar las operaciones aritméticas y algebraicas de los números racionales, ya vimos que no representan pasos extraordinarios para realizar la amplificación o simplificación de las fracciones originales.
También debemos tener presente que existe una representación de las fracciones impropias de manera que el número mixto nos indica la distribución de varias partes de los elementos que conforman el conjunto total, en este caso tendremos que el numerador es un número mayor que el denominador.
Fuentes
- ¿Sabes qué es una fracción equivalente?, smartick blog
- Números fraccionarios, ecured
- ¿Cuáles son las partes de un número fraccionario y ejemplos?, aleph blog
- Imagen de portada, Manuelzapata04

