Ya es bien sabido que la Matemática se constituye en una herramienta inseparable a las distintas disciplinas de las ciencias naturales, en especial guarda estrecha relación con la Física y se aplica para explicar los diferentes fenómenos u acontecimientos que ocurren en nuestra naturaleza. Un ejemplo muy sencillo es cuando se analiza el movimiento de un automóvil que se desplaza de una ciudad a otra con una velocidad constante de 80 Km/h en un periodo de tiempo de 4 horas, por lo que se puede determinar el valor de la distancia recorrida en diferentes intervalos de tiempo mediante la aplicación de ecuaciones físicas o haciendo uso de la integral definida.

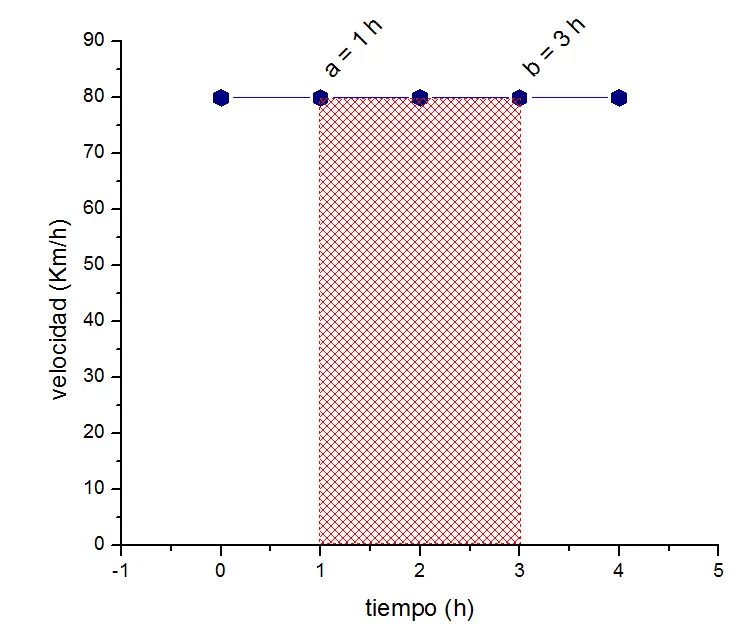
Y es que podemos utilizar ejemplos simples y sencillos de cualquier función que relacione una dependencia entre variables susceptibles a ser medidas, como por ejemplo, el desplazamiento de un vehículo con velocidad constante, por lo que en una gráfica de velocidad y tiempo se espera que sea una línea horizontal que me indica una velocidad constante de 80 Km/h en un intervalo de tiempo de 4 horas, pero podemos seleccionar cualquier intervalo de tiempo intermedio y esperar obtener el mismo valor de la velocidad.

Esta situación sólo aplica a ciertos rangos de tiempo, por lo que la función puede estar acotada o aplicar restricciones sobre el tipo de movimiento con velocidad contante o variable, por lo que puede obtenerse una gráfica que represente una situación más amplia, en un rango de tiempo extenso, que involucre varias situaciones reales como las velocidades en ambos sentidos de una trayectoria, tal como se observa en la siguiente figura:

Función:

v(t) = d·t, con las especificaciones del ejemplo en cuestión que la velocidad es constante, v(t) = k a) v(0) = d₀/0 b) v(1) = d₁/1 c) v(2) = d₂/2 d) v(3) = d₃/3 e) v(4) = d₄/4 v en (Km/h), d en (Km) y t en (h).

Como el parámetro velocidad es constante, entonces:

Gráfica velocidad en función del tiempo

podemos determinar el área bajo la curva a partir de una figura geométrica, como un rectángulo, multiplicando la BASE: (t) por la ALTURA: (v).

Este resultado tiene unidades de distancia o si trabajamos con la forma vectorial, se corresponde con el desplazamiento del automóvil durante la primera hora de viaje, así que en 1 hora recorrió 80 Km. Es compatible con la velocidad de 80 Km/h, recorre 80 kilómetros en 1 hora, ¡es lógico!

Sustituyendo en la relación b) v(1) = d₁/1

Integral definida

Toca el turno del concepto fundamental de la integral definida para determinar la distancia recorrida en intervalos de tiempo definidos, recordando que en este caso en particular, la velocidad es constante y para facilitar la notación matemática usaremos d = r para la forma vectorial y d = r cuando se trate de un escalar como la distancia recorrida.

Integrales:

la notación básica es ʃ dx = x + C, siendo la x una variable. En nuestro caso v(t) = k ʃ v(t) dt = v ʃ dt = v t + C
con la observación que debemos incluir los límites de la integración, que estará definida por los extremos t_final menos t_inicial

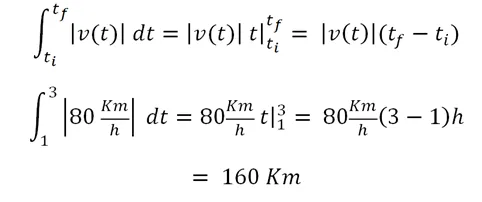
Por supuesto que este resultado es en un intervalo de tiempo, entre 1 h y 3 h, es decir que en 2 horas recorrió 160 Km. Nuevamente es lógico pensar que si en 1 hora recorre 80 Km, entonces en 2 horas recorre 160 Km y si sumamos los intervalos entre 0 h y 1 h (80 Km) más el intervalo 1 h y 3 h (160 Km), pues obtendremos los 240 kilómetros recorridos en 3 horas de viaje.

Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de janjf93: Portada con el tema de Integrales Definidas
• Video YouTube: Integrales definidas
• Wikipedia: Integración

Las funciones matemáticas son expresiones que relacionan
las variables de una igualdad,
así que invariablemente encontraremos alguna solución