En el siguiente artículo se explicará de forma detallada uno de los elementos claves en el diseño de redes Microondas, específicamente analizaremos el Inversor, entendiéndose este como un elemento pasivo en las redes propiamente dichas ; así mismo profundizaremos aspectos técnicos como lo son sus propiedades, formas e interpretaciones que existen para caracterizar este dispositivo a través de sus matrices de parámetros Z, Y y S.
En concreto el funcionamiento de un inversor es bastante simple, lo definimos como un elemento el cual al aplicarle en su terminal de entrada una impedancia o admitancia conocida, será capaz de proveer una impedancia o admitancia inversamente proporcional en su terminal de salida.
Aclaración: No existen inversores que convierten impedancia a admitancia, simplemente teniendo una de estas puede generar un valor inversamente proporcional para cada caso en específico.

Figura 1. INVERSOR DE IMPEDANCIA/ADMITANCIA --- Fuente: Elaboración propia.
Zin es la Impedancia de la entrada y ZL la impedancia del otro extremo, lo mismo para Yin y YL.
En cuanto a sus propiedades podemos primeramente identificar que consta de una red de dos accesos como se ilustra en la Figura 1, además se le suma que es una red pasiva sin perdidas, es decir no disipa energía; es del tipo reciproca por lo que no se verá afectado el resultado si la carga es aplicada en el acceso 1 o 2, posee parámetros de simetría puesto que los elementos S11 y S22 (Z11 Y Z22 según sea el caso) coincidirán en magnitud y como punto de inflexión muy importante, el parámetro S11 debe ser un valor real. Basándonos en todas estas propiedades podemos decir que estamos en presencia de un inversor.
Ahora bien, la forma que tenemos para caracterizar estos elementos viene dada por el cálculo de la constante de proporcionalidad de la inversión la cual evidenciaremos como K cuando nos refiramos a la Impedancia y J cuando especifiquemos una admitancia, en ambos casos se considerara un valor real y positivo.

Atendiendo a las dimensiones de cada caso en específico, K y J adoptaran valores de Impedancia y admitancia respectivamente.
Interpretaciones de las Matrices de Parámetros Z ,Y, S
Las matrices de un inversor vienen dadas de las siguientes maneras:

Figura 2. MATRICES DE PARÁMETROS Z Y PARÁMETROS Y --- Fuente: Elaboración propia.
De las cuales podemos interpretar las siguientes premisas:
Los elementos Z11 Y Z22 serán iguales a 0, por lo que si tenemos una red pasiva, recíproca y sin perdidas automáticamente se concluye que estamos en presencia de una red inversora pues seguramente el Z21 será imaginario puro y efectivamente el valor de Z12 (Al existir reciprocidad en la red) será igual al Z21 coincidiendo así con el valor de la constante de proporcionalidad que se denota como K.
Entonces conocida K, el cálculo de la matriz de impedancia se hace inmediato. De forma análoga ocurre con la matriz de Y.
En cuanto al análisis para la matriz de dispersión S, tenemos un razonamiento bastante parecido:
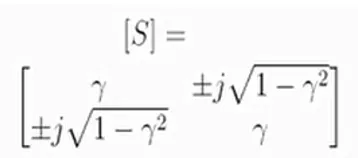
Figura 3. MATRIZ DE PARÁMETROS S --- Fuente: Elaboración propia.
Se hace énfasis nuevamente que si tenemos un red con las propiedades previamente analizadas es decir, pasiva, reciproca y sin perdidas, los elementos S21 Y S12 serán iguales, así mismo S11 Y S22 por simetría consideran y además si corresponden con un valor real , nuevamente entendemos que la matriz representa un inversor.
Como en el ejemplo de la matriz Z, podemos relacionar el valor ɣ directamente con las constantes de proporcionalidad K y J, la cual viene dada por la siguiente expresión:
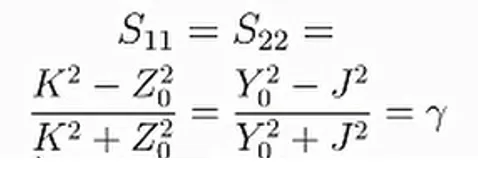
Nuevamente, conocida J o K el cálculo de los parámetros de la matriz S se hace inmediato.
Fabricación de Inversores
Partiendo de Elementos Concentrados
Para la fabricación de redes inversoras se consideran las propiedades de reciprocidad, sin perdidas y pasiva, por lo que partiendo de un diseño con elementos concentrados que reúnan estas características se puede proceder sin muchas complicaciones; en cuanto a estos elementos podemos destacar bobinas y condensadores básicamente.
Ahora bien estableciendo un diseño en el dominio de la Impedancia pudiéramos realizar un circuito de equivalente en T con tres elementos y además pudiera ser representando en una matriz Z, quedándonos de la siguiente manera:

Figura 4. EQUIVALENTE DE UN INVERSOR PARA UN ARREGLO EN T --- Fuente: Elaboración propia.
Muy importante siempre lograr que el Z11 y Z22 sean iguales a 0 (principio del inversor) por lo que las expresiones que gobiernan al equivalente en T en cada uno de sus elementos, al ser Z11 Y Z22 nulos, pudiéramos sintetizar el diseño visto desde sus componentes reactivos como vemos a continuación
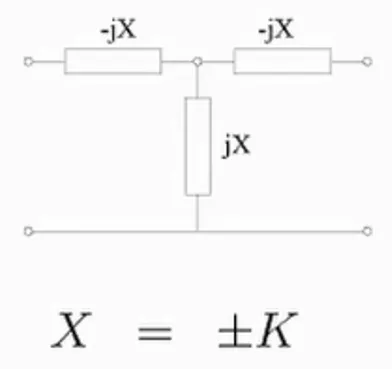
Figura 5. EQUIVALENTE EN T ; VISTA DE COMPONENTES REACTIVOS --- Fuente: Elaboración propia.
Recordemos entonces que Z12 es un valor imaginario proporcional a la constante de inversión K. Por tanto los tres valores reactivos resultantes serian equivalentes en modulo y cambiarían de signo respectivamente.
La reactancia en el elemento inferior podrá ser positiva o negativa, es decir, puede tener comportamiento capacitivo o inductivo, sabiendo que si condicionamos a los 2 elementos de la parte superior con caracteres capacitivos (condensadores) el tercer elemento deberá ser una bobina, y viceversa.
El mismo razonamiento lo aplicamos para el caso de las admitancias, esta vez partimos de un equivalente en pi.

Figura 6. EQUIVALENTE EN PI DE UN INVERSOR --- Fuente: Elaboración propia.
A partir de este equivalente pudiéramos calcular el valor de los elementos concentrados que sintetizarían a un inversor.

Figura 7. EQUIVALENTE EN PI DE UN INVERSOR ; VISTA DE COMPONENTES REACTIVOS --- Fuente: Elaboración propia.
Partiendo de Elementos Distribuidos
También es posible diseñar inversores a partir de elementos distribuidos, como lo son las líneas de transmisión.
Por definición recordemos que una línea de transmisión de longitud λ/4 es un inversor de impedancia; la relación existente para una línea de λ/4 entre la impedancia de entrada y la impedancia de carga será inversamente proporcional mientras que para el caso de la impedancia característica será directamente proporcional al cuadrado de la misma.
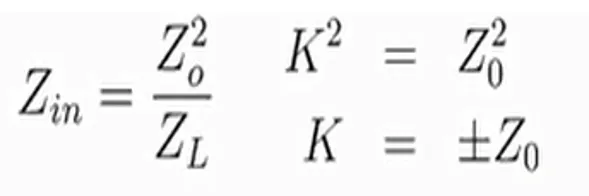
Donde:
Zin= Impedancia de entrada
Zo=Impedancia característica
Si equiparamos este razonamiento con las formas de caracterizar a un inversor, las cuales detallamos anteriormente, vemos que el valor de K coincide con Zo.
A continuación se evidencian los modelos para un inversor empleando línea de transmisión:
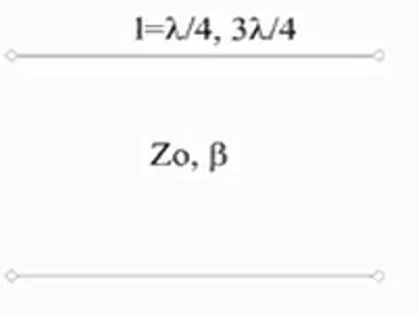
Figura 8. MODELO DE INVERSOR APARTIR DE UNA LÍNEA DE TRANSMISIÓN --- Fuente: Elaboración propia.
Como se puede apreciar, independientemente la longitud adicional que tenga una línea de λ/4 su comportamiento será del tipo inversor sin excepción y esto se interpreta de forma que si identificamos una línea en la carta de Smith y agregamos λ/2 es como si diéramos una vuelta completa y volvemos al mismo punto.
El modelo de una línea de transmisión visto en un equivalente de elementos concentrados puede ser interpretado por medio de una matriz de impedancia tal cual lo vimos anteriormente:

Pero ahora Z12 estaría representado por:
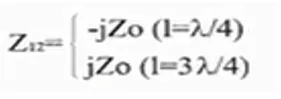
Z12 será de signo negativo para una línea de λ/4 y positivo para una línea de λ/4 a los cuales se le añaden λ/2.
Fabricación mixta; Elementos Concentrados y Distribuidos
De igual forma puede darse el caso que empleemos las líneas de transmisión y los elementos concentrados para la elaboración de redes inversoras.
Combinando elementos que guarden las propiedades anteriormente analizadas podemos emplear un diseño mixto; pues bien, una red candidata que cumpla estos parámetros seria:
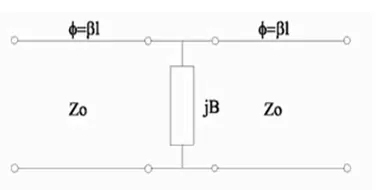
Figura 9. MODELO MIXTO DE INVERSOR: ELEMENTOS CONCENTRADOS Y DISTRIBUIDOS --- Fuente: Elaboración propia.
Vemos en la imagen elementos sin perdidas, recíprocos y pasivos, la susceptancia B (parámetro Z12 imaginario) en paralelo con 2 líneas de longitudes iguales para respetar la simetría validan este arreglo como un candidato a un inversor.
Ahora bien cómo podemos evidenciar , la red descrita cumple a cabalidad las premisas de un inversor, solo estaría faltando que el parámetro S11 de la Matriz S sea real.
Para calcular el parámetro S11 de esta red consideramos la siguiente expresión:

Dónde: w será la frecuencia angular, v la velocidad de propagación de la línea y l la longitud de la línea.
Vemos que la fase de S11 ya ha sido localizada, donde el argumento fasorial está relacionado con el valor de la susceptancia y Φ sería la longitud eléctrica de las líneas.
Entonces para que S11 fuese real una solución sería que Φ y el otro argumento sean iguales, de esta manera obtendríamos un valor negativo pero real, por lo que estaríamos cumpliendo con la condición de inversor.
Por tanto tenemos la siguiente expresión que iguala estos términos:
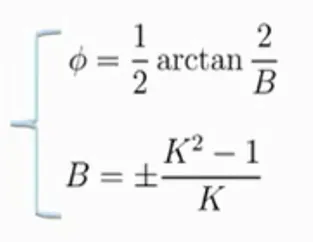
Una vez establecida la simetría y adicionalmente agregamos un valor de susceptancia B que guarde una relación con Φ mediante la expresión descrita, podríamos considerar vinculación entre la susceptancia y la constante de proporcionalidad K, es decir, están directamente involucradas.
Entonces, una vez que hemos deducido las ecuaciones, pudiéramos sustituir el valor de K que emplearíamos y así determinar el valor de la susceptancia, para finalmente calcular la longitud de las líneas.
Análisis de casos específicos
Considerando lo anteriormente dicho, se nos presentan dos situaciones: El primer caso sería cuando el valor de la susceptancia tuviese carácter capacitivo, la susceptancia propiamente dicha será positiva y considerando la relación que estudiamos entre la línea eléctrica y B , recordemos:
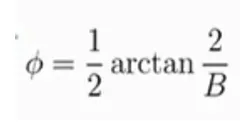
se infiere que el valor de la longitud será positivo, todo normal hasta aquí.
El asunto de reflexión seria el segundo caso, es decir, si el valor de la susceptancia tuviese carácter inductivo, por lo que B seria negativa y por ende la longitud del cable seria negativa , físicamente irracional, mas sin embargo esto sirve para interpretar lo siguiente:
Si se pudiera conectar el inversor por ambos terminales a líneas de transmisión de longitudes grandes de manera tal que el valor negativo se entiende como un recorte de las líneas externas que conecta, seria procedente o implementable en principio.
Sintetizando los arreglos que hemos analizado, procedemos a definir cuál sería el más óptimo, por lo que valoraremos la respuesta en frecuencia de la fase del parámetro S11, recapitulemos entonces la expresión que rige a S11:
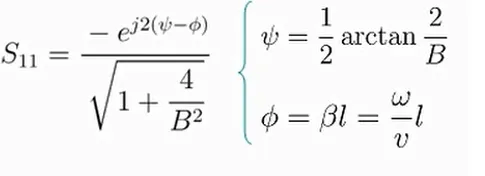
Teniendo esta ecuación para S11 se procede con el análisis en frecuencia; dado el signo menos en la expresión original y los términos fasoriales , operamos de la siguiente forma:

Y simplemente sustituimos los ángulos correspondientes:
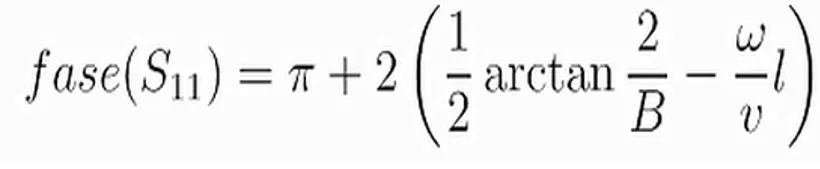
Ahora bien, tomemos en cuantas dos situaciones:
La primera seria cuando la constante K fuese muy pequeña

Resulta entonces que el valor de la susceptancia B seria el in verso de K .
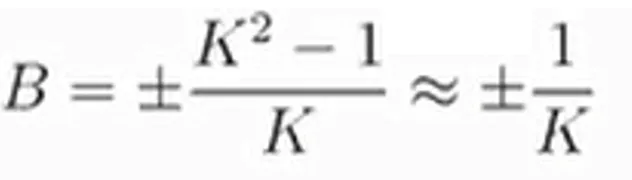
Se asume entonces que el valor de la susceptancia en términos absolutos será mucho mayor a la unidad.

Para la situación opuesta, es decir, que el valor de K sea mucho mayor a la unidad :
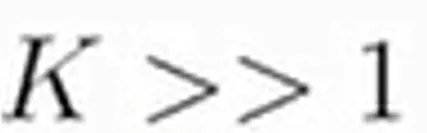
En este caso vemos que los valores de B se aproximarían a los de K .

Y al igual que en el caso anterior los valores absolutos de B serían mucho mayor a la unidad.
Asumiendo que estamos en cualquiera de estas dos situaciones y que la susceptancia sería un valor mucho más grande que la unidad, resultaría que la expresión de Φ en función de B se aproxima como el inverso de B :

Recordemos que la arcontangente del argumento cuando el argumento es muy pequeño se aproxima al argumento propiamente dicho.
Sustituyendo entonces nos queda una expresión más simplificada:

Y así tendríamos la expresión que gobierna la fase de S11.
Llegado a este punto nuevamente tenemos dos vertientes:
1) qué pasa si la susceptancia tiene carácter inductivo?, es decir , es una bobina :
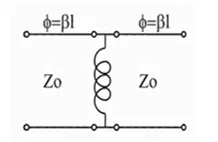
Figura 9. EQUIVALENTE PARA UN INVERSOR INDUCTIVO EN PARALELO --- Fuente: Elaboración propia.
La dependencia con la frecuencia de una bobina esta dada por:
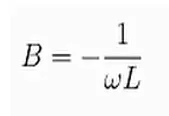
Donde L es la magnitud de la bobina y w es la pulsación angular, sustituyendo en la ecuación de fase de S11 nos queda:

Cuando será esto un inversor?
Partiendo de los análisis previos habíamos dicho que la longitud debería ser negativa, la cual viene dada por el producto del valor de la Bobina y la velocidad de propagación en la línea:
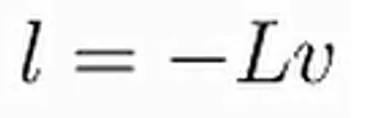
Asumiendo que podemos conseguir longitudes negativas mediante la resta de líneas de transmisión externas, resulta que la fase del S11 siempre va a ser real, a cualquier frecuencia, por lo que se concluye para este caso que la configuración de bobina en paralelo se comportara como un inversor de banda ancha (a cualquier frecuencia)
2) qué pasa si la susceptancia tiene carácter capacitivo?, es decir , es un condensador:
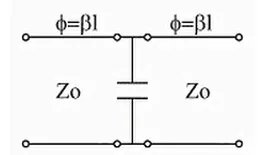
Figura 10. EQUIVALENTE PARA UN INVERSOR CAPACITIVO EN PARALELO --- Fuente: Elaboración propia.
La susceptancia para un condensador está dada por:
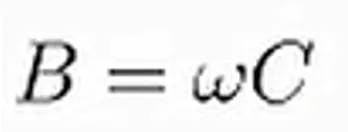
Donde C es la magnitud del condensador .
Sustituyendo en la expresión de la fase:

De manera que aunque la longitud en este caso será positiva solo a una determinada frecuencia se anulara el término de la derecha, por tanto S11 solo será real a una frecuencia en específico, es decir que a esa frecuencia tendríamos un inversor, de banda estrecha específicamente.
Dado los comportamientos en frecuencia se evidencia que el arreglo de bonina en paralelo es superior al de condensador en paralelo puesto que el primero actúa en todas las frecuencias.
Espero esta información haya sido de su agrado, estaré contribuyendo con más material de calidad y aporte científico para la comunidad, por lo cual espero sus impresiones y demás opiniones.
Referencias
DISEÑO DE INVERSORES DE IMPEDANCIAS DE MICROONDASlineas-de-transmicion-rodolfo-neri-vela.
MICROONDAS-UPV
Microwave impedance measurements and standards
