Saludos cordiales mis estimados lectores, un gusto el volver a compartir con ustedes una nueva entrega!
En esta oportunidad he decidido hacer un paréntesis en medio de mis continuas publicaciones referentes a las comunicaciones ópticas. La temática a abordar en este texto estará basada en el estudio de los números complejos, pero con un enfoque didáctico que contrasta mucho con las formas “tradicionales” que se tienen para el análisis de este amplio conjunto de números.
El análisis matemático ha servido a lo largo de la historia para formular objetivamente variedad de fenómenos que se desarrollan en los distintos niveles de la naturaleza, en ocasiones las interpretaciones de los teoremas resultan un tanto abstractas para el entendimiento y como si esto no fuera poco, muchas veces se han de recurrir a números que “no existen” para definir uno que otro caso en específico, por ejemplo, en Telecomunicaciones y en la ingeniería en general, emplear números complejos para definir el comportamiento de los campos electromagnéticos, fluctuaciones de voltaje, corriente y señales, son algunos de los casos que sirven para ilustrar el ejercicio de este conjunto.
Sin embargo, resulta muy interesante plantearse la pregunta: ¿Qué son estos números realmente?, esto suena muy trivial en realidad, pero en honor a la verdad, comencemos a explorar este fascinante campo:
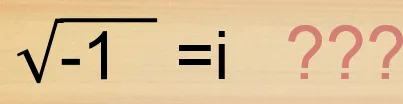
Figura N°0 Elaboración Propia
En nuestra formación académica, específicamente en el ciclo básico profesional en el área de cálculo y matemáticas, nos han convencido de que los números complejos surgen cuando nos topamos con una función del tipo x^2+1=0 y que al resolver esta ecuación se tiene que x vale √(-1) , pero la raíz cuadrada de un numero negativo no existe, por tanto se le atribuye la letra “i” (o j según el autor). En fin, una concepción bastante profana, si bien es cierto que estrictamente hablando esto es así, solo se está viendo una cara de la moneda.
Para efectos de la explicación que a continuación se presenta, tenga en cuenta solo las rotaciones de un vector que para este contexto se identificaran con la letra R; en la figura 1 se muestra un plano cartesiano xy (el de toda la vida), paralelo al eje x se tiene un vector cuya magnitud es 1 y por tanto su módulo será 1, esta flecha nos servirá como una referencia inicial y lo denominaremos ‘vector de partida’:
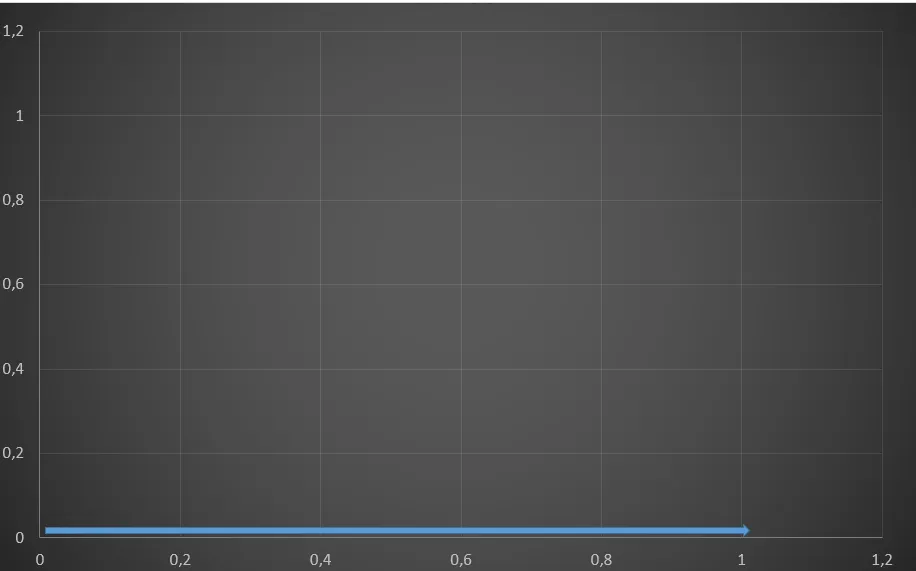
Figura N°1 Vector de Partida – Elaboración Propia
Partiendo de esta disposición inicial se pueden desprender muchas cosas interesantes. Se plantea en principio la operación: rotar 90 °:
Al aplicar una rotación de 90° (en sentido anti horario) se obtiene el vector resultante:
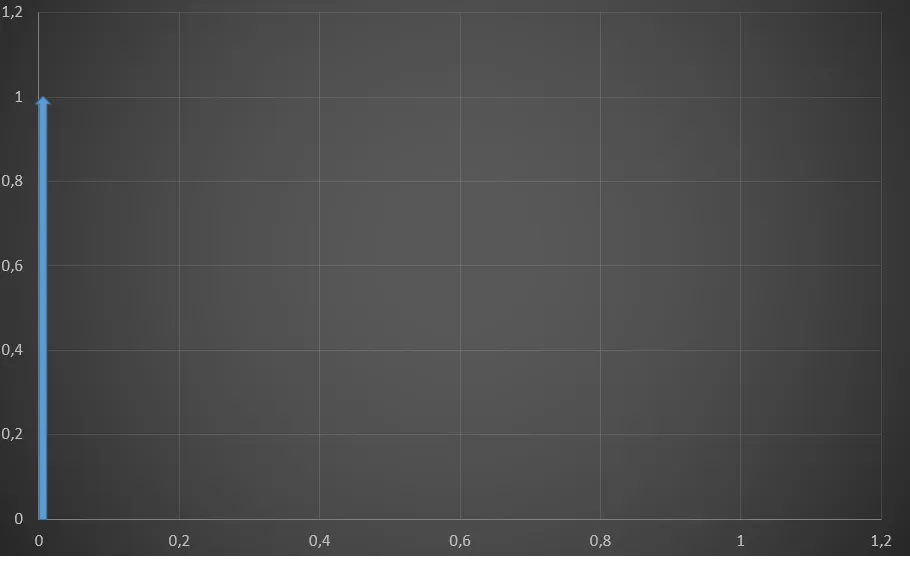
Figura N°2 Rotación de 90°– Elaboración Propia
De forma analítica se puede decir entonces:

Donde R representa la operación rotación.
Como se ha podido apreciar es una operación sumamente sencilla, para el siguiente caso se efectúa la operación rotar 180°. De forma análoga al primer caso, se tiene que:
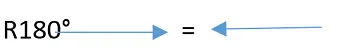
Ahora bien, dada cualquier operación de rotación, esta puede ser expresada en función de argumentos de 90°, por ejemplo: R180°=R90°R90°
Efectivamente, esta operación de rotar 180° se traduce en aplicar dos veces la operación rotar 90°, visto de otra forma:

Si se observa con un poco más de detenimiento el vector rotado, se puede decir que basta con multiplicar por -1 el vector de partida, con esta operación se estaría cambiando el signo de la componente vectorial y en definitiva el vector resultante sería el mismo pero en dirección contraria, sintetizando:
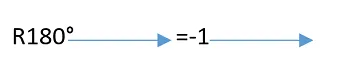
Si se considera otra operación, concretamente rotar 270°, rápidamente se obtiene:
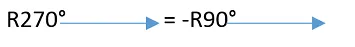
Reescribiendo:
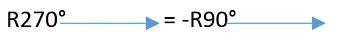
Es decir, girar 270° es equivalente a girar 90° y cambiar de signo el sentido del vector resultante.
Finalmente, la operación R360°(la más sencilla) seria no hacer nada, o más formalmente multiplicar por 1 al vector de partida.
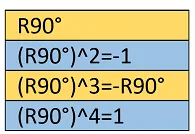
Tabla N°1 Resumen de operaciones de rotación – Elaboración Propia
Nótese que hasta el momento lo único que se ha hecho es expresar operaciones de rotaciones vectoriales en función de ángulos de 90°, pero bien pudiera plantearse: ¿se pueden hacer rotaciones de 45° expresadas con ángulos de 90°? Y la respuesta es un rotundo SI.
Partiendo del vector de referencia que se ha definido en principio, se tiene que:
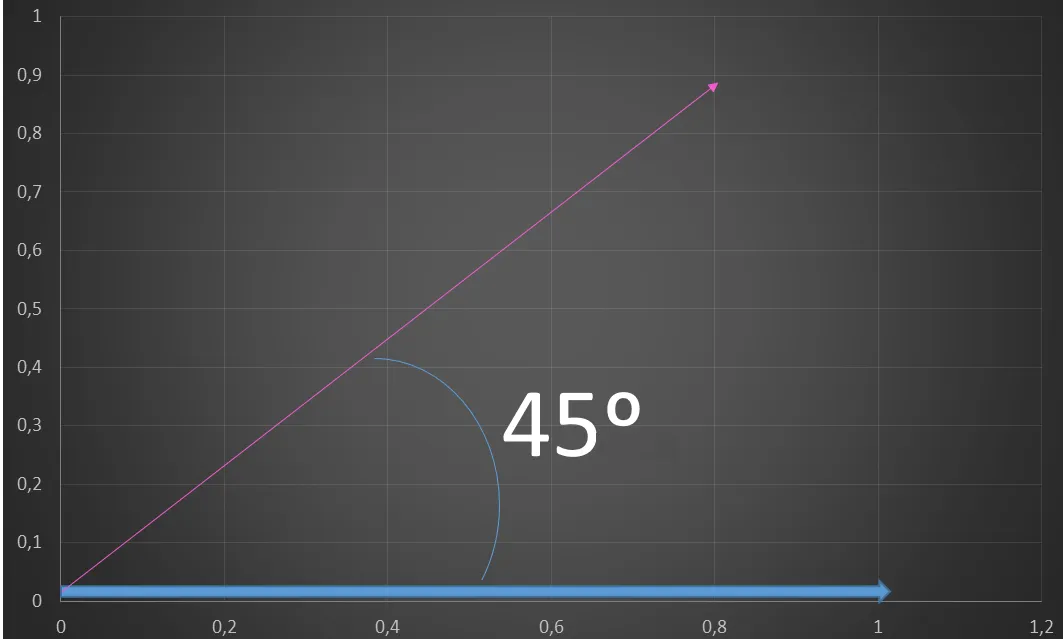
Figura N°3 Rotación de 45°– Elaboración Propia
Pero, ¿qué significa este vector?, si se aplica una suma de vectores de forma gráfica se sabe que:
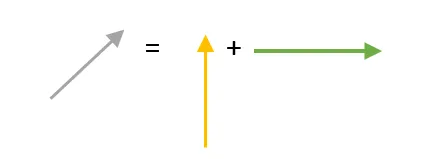
Se debe cumplir entonces:
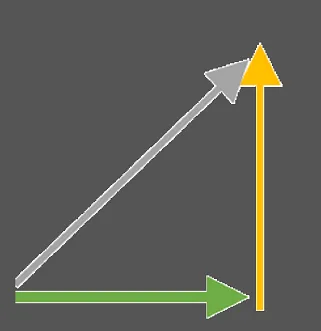
Figura N°4 Suma grafica de Vectores – Elaboración Propia
Por tanto rotar 45° el vector de partida puede ser expresado de la siguiente forma:
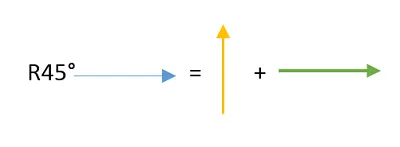
¿Y cuánto valen las flechas del segundo término de la igualdad?
Aplicando un poco de geometría y observando la figura 4 se asume un triángulo rectángulo, por tanto el vector resultante se deduce como la hipotenusa y las otras dos flechas serian cateto opuesto y adyacente respectivamente; como el ángulo que forma la hipotenusa y el cateto opuesto es de 45° los lados del triángulo serán iguales (cateto opuesto y ateto adyacente), recordar que esta hipotenusa mide 1 (por la conveniencia que se estableció en principio), por Pitágoras se tiene que:
h2=co2+ca^2 ; (co=ca) , (h=1)
h= hipotenusa; co= cateto opuesto; ca=cateto adyacente
Desarrollando se tiene entonces que cada vector equivale a 1/√2
Sustituyendo en la fórmula de R45° :
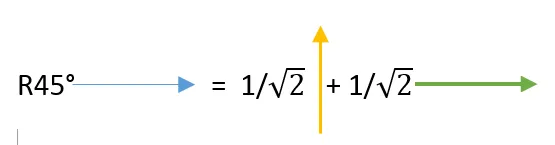
Llegado a este punto se puede generalizar la expresión en función de vectores cuyas magnitudes sean 1:
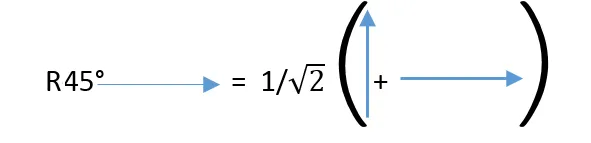
Cabe destacar el uso de los colores para cada flecha; al aplicarse factor común se han obtenido dos vectores cuyas magnitudes son 1, resultando así en vectores que ya han sido analizados, es decir, se ha logrado expresar una rotación de 90° más un vector de partida.
Sustituyendo:

Se ha demostrado que una rotación de 45° puede estar compuesta por elementos que comprendan rotaciones de 90°. Antes de proseguir con el desarrollo, se estudia un último ejemplo solo para corroborar la consistencia del análisis, asumamos la operación R30°:
Para determinar el valor de los lados de este nuevo triangulo, aplicamos trigonometría básica:
Determinando el cateto opuesto
cosθ= co/h
co= cosθ= cos(30°)
Determinando el cateto adyacente:
senθ= ca/h
ca= sen30°
Obtenidos los valores de cada vector se procede como en los casos anteriores:
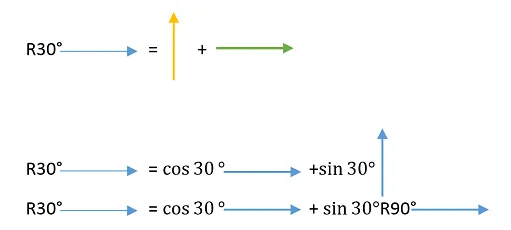
Simplificando las flechas nos queda una expresión más resumida:
R30°= cos30°+ sin(30°)R90°
Entonces, para expresar cualquier rotación basta con generalizar de la siguiente manera:
Rθ= cosθ + sinθ R90°
Analizado lo anterior, retomemos la función que da origen a toda esta polémica: x^2+1=0 , pues bien, ya es sabido que las raíces cuadradas negativas no existen, pero si planteamos la operación desde una óptica similar al de las rotaciones surge lo siguiente:
x^2=-1 : en este caso la pregunta es que numero multiplicado por sí mismo da como resultado -1
En el dominio de las rotaciones vectoriales la pregunta se reformula : ¿Qué operación multiplicada por si misma da -1? . Con el estudio de este texto se pudiera asumir entonces que esta operación sería R90°, al aplicar dos veces esta operación a un vector de partida se tendrá el mismo vector pero con sentido opuesto, o como se decía anteriormente, será como multiplicar por -1, por consiguiente, resulta valido decir que la solución a la ecuación x^2+1=0 es x= R90°. Por convención matemática esta operación R90° es definida como “i” y no es más que la representación de dicha operación aplicada a un vector.
Así como en las disposiciones iniciales de este texto donde analizamos el comportamiento de las rotaciones, el número imaginario i tiene sus propiedades:

Tabla N°2 Propiedades del Numero i – Elaboración Propia
Entonces …
¿Qué es un número complejo?
Un número complejo es un número r multiplicado por una rotación de ángulo θ :
Z=rRθ.
Concretamente esta es una de las maneras que se tienen para escribir un complejo y lleva el nombre de “Forma Polar”.
y esto, ¿qué significa?
Simplemente es una operación, la cual rotara conforme a un ángulo y el vector resultante estará definido en magnitud por el valor de r. por ejemplo: Z=5R50°
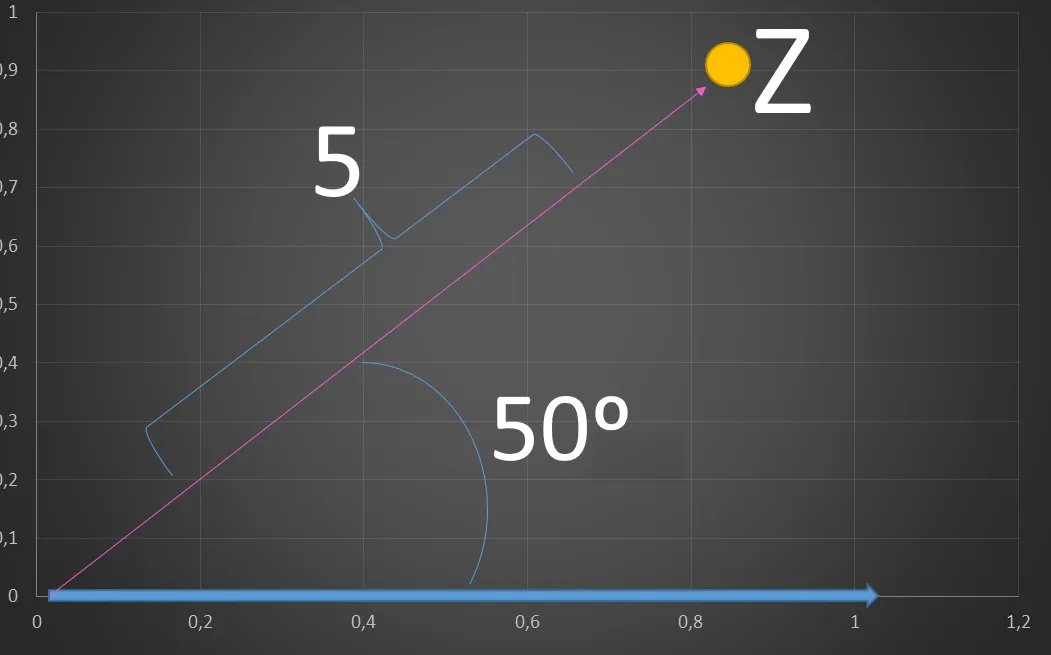
Figura N°5 Representación Gráfica de Z=5R50° en el plano complejo– Elaboración Propia
Ese punto amarillo en la gráfica seria el número complejo Z.
Un complejo también se puede plasmar en función de coordenadas cartesianas o rectangulares para que adopte la forma Z= a+ib, donde a representa la parte real y b la parte imaginaria. Para determinar los coeficientes a y b se retoman las deducciones de trigonometría que se realizaron previamente:
a=rcosθ ; b=rsinθ
Z= 5(cos50°+ i sin(50))
Z= 3,214 + i3,83
Visto en la gráfica de coordenadas rectangulares:
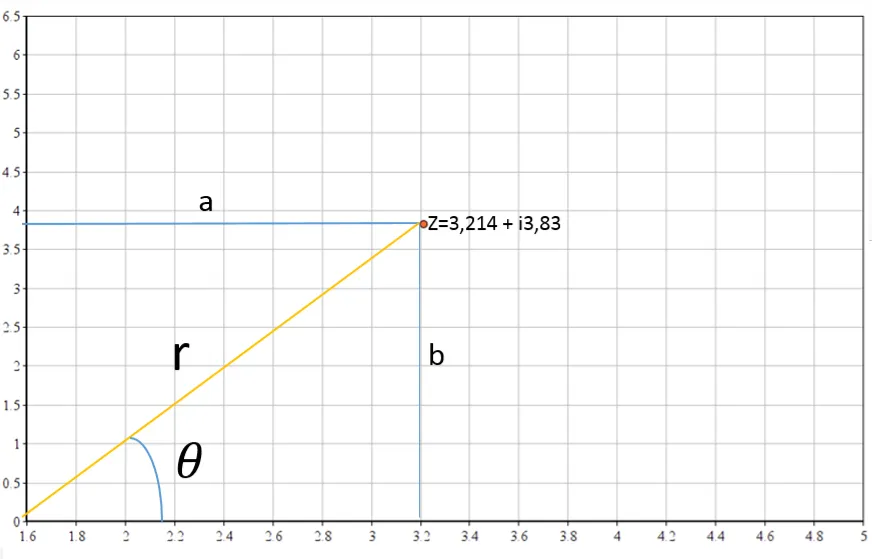
Figura N°6 Representación Gráfica de Z= 3,214 + i3,83 en el plano cartesiano– Elaboración Propia
Si se desea retornar a la forma polar, es decir, Z=rRθ se debe calcular el valor de r que como se podrá observar es una hipotenusa y el valor del ángulo el cual esta está definido por la tangente inversa de la componente imaginaria y la componente real:
r=√(a2+b2 )
θ=tan^(-1)(b/a)
¿Y con esto está todo cubierto?
Resulta que los números complejos pueden ser acomodados haciendo uso de una expresión sumamente elegante y que facilita el cálculo de las operaciones entre este conjunto, antes de develar esta función (seguramente ya muchos la sepan) se consideran algunas propiedades de la función seno y la función coseno:
sinθ=θ θ≪1
cosθ= 1 θ≪1
El próximo ingrediente a tomar en cuenta será el famosísimo número “e”, el cual se define como:
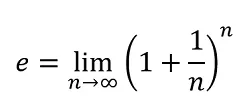
Esta es una función que se aproxima al valor del número e (2,71828…) y depende de cuán grande sea n. Una de las variantes que tiene la función exponencial es la siguiente:
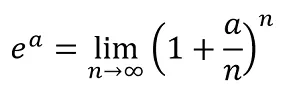
En otras palabras, cualquier “cosa” que se eleve al número e tiene la forma (1+a/n)^n
Donde ‘a’ representa cualquier número, para el caso que nos interesa pudiera ser también un numero imaginario.
Retomamos la ecuación que definía una rotación vectorial en función de senos y cosenos, esta vez expresada en radianes:
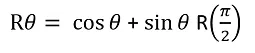
Para el caso de una rotación de 30°, que en radianes seria π/6 , esto se puede rescribir en fracciones iguales que equivalgan a la operación en cuestión, por ejemplo en 3 partes iguales (10°+10°+10°), nos queda entonces:
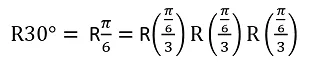
Pues bien, para cualquier división de ángulo se establece la forma:
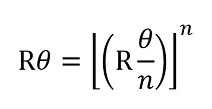
Entendidas estas concepciones se procede a unificar lo aprendido:
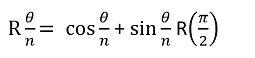
Cuando n tiende a infinito θ/n será muy pequeño, por tanto el coseno será aproximadamente 1 y el seno tomara el valor del argumento (θ/n) como se decía anteriormente. Sustituyendo:
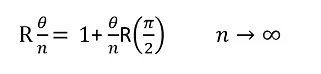
Para girar el ángulo completo:
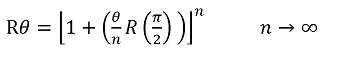
-¿Y a que se parece esto? -, justamnte a : 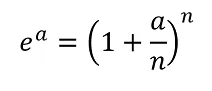
Finalmente:
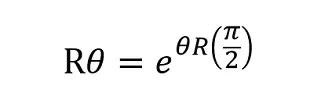
Expresándolo en función de R90°:
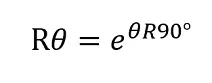
Y para verlo en la notación por excelencia (la más reconocida):
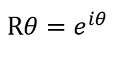
Por tanto, la parte imaginaria de un número complejo se lee:
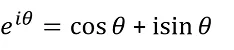
Para expresar un número complejo de la forma Z=rRθ:
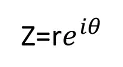
O bien:
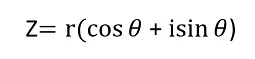
Y con esto se ha podido explicar la relación del número e con los números complejos así como la interpretación que se le da a este conjunto de números y su procedencia.
Existen múltiples formas de llegar a las conclusiones que se obtuvieron en este texto, unas más rigurosas que otras, lo cierto del caso es que con este análisis resulta muy fácil la comprensión de un tema que en principio parece tan abstracto, pero si se plantean bien las cosas (y con un toque de didáctica) todo resulta muy claro.
Nos vemos en una próxima oportunidad, un saludo y muchos éxitos…!
Referencias
Una Introducción a los Números Complejos
El numero e en el calculo elemental - Escuela de Matemática (UCV)
El numero e en el calculo elemental - Escuela de Matemática (UCV)

