Hello its me again Drifter Programming! Today we get into Java Graphs again talking about the Maximum Flow Problem and how we solve it using the Ford-Fulkerson Algorithm! This algorithm depends on and uses an Graph Traversal algorithm (DFS or BFS) and so I suggets you check out those first if you haven't already! I will implement the main algorithm using the Breadth-First-Search (BFS) algorithm. So, without further do let's get started!
Max Flow Problem:
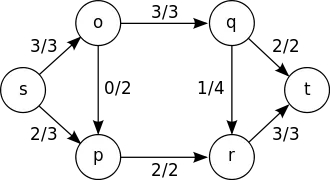
Suppose a flow network were each edge has a maximum flow capacity. The max flow problem is all about finding the maximum flow that we can get when going from a single-source vertex to a destination vertex. An edge can't exceed it's capacity.
This information can be useful in computer networks to find the maximum bandwidth that an connection can have or even at finding the maximum water capacity of an water supply network!
This problem can be represented as an Graph again were each Edge has a maximum flow capacity or weight and we then try to find the maximum flow using an algorithm. I will use the Adjacency Matrix representation that we also used in the Floyd Warshall algorithm, but I will change the initialization of the Edges (edge doesn't exist) to zero instead of MAX_VALUE or infinity. In the same way we will use the BFS Algorithm, but change it so that it checks for an path from one specific source vertex to an destination vertex and also stores the path information in an parent array.
The main algorithm is the Ford-Fulkerson Algorithm that does the following:
- It gets a graph and source and destination vertices as Input
- It creates an residual graph initialized equal to the input graph and initializes maxflow=0
- It loops as long as BFS (or DFS) returns a path from source to vertex and
- Finds the maximum path flow
- Updates the residual graph and reverse edges along the path
- Adds the path flow to the maxflow
4. Lastly returns the max flow
There is also another algorithm based on this one called Edmonds-Karp, but I will not cover it. You can check out some information here in wikipedia.
Ford-Fulkerson Java Implementation:
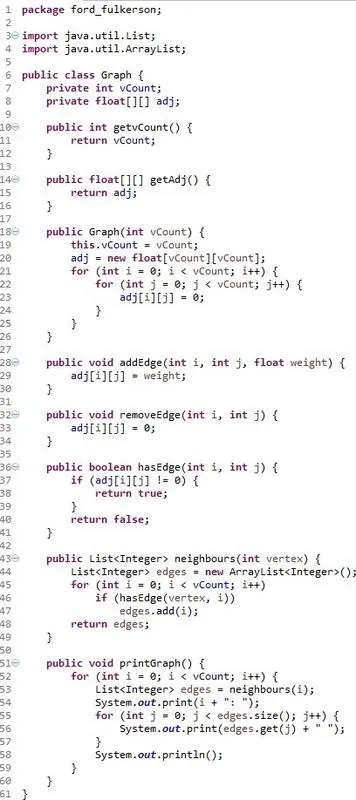
As I already told you we will use the Graph from last time, but tweak it so that it initializes edges as 0 instead of Infinity. So, we only need a Graph class that will do all the Graph work for us. The main algorithms BFS and Ford-Fulkerson will be inside of the TestGraphs class as always.
So, the classes look as following:
Graph Class:
BFS Algorithm:

Ford-Fulkerson Algorithm:

The rest of the TestGraphs class:
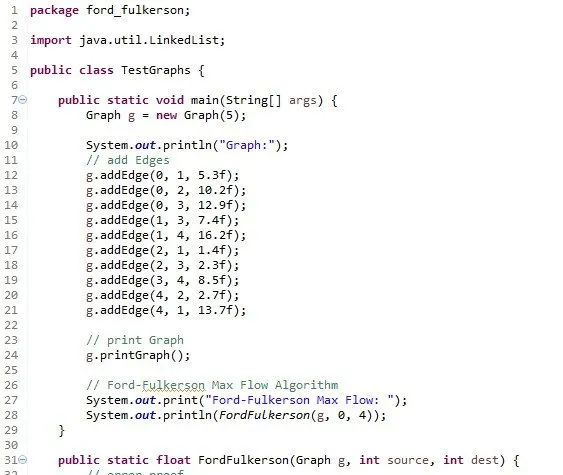
The Console prints out:

And this means that the maximum flow from 0 to 4 is 15.2.
You can download the code in the following links at pastebin:
TestGraphs class that contains the algorithms also
You again can put them in a package with the name I put or remove the declaration.
And this is actually it for today!
I have two more algorithms that have to do with finding Hamiltonian and Eulerian Circuits in a Graph, but I haven't implemented them yet and so it might take some time! If you have any suggestions for other algorithms that I should cover don't be shy just tell me! :)
Bye!
