
Image source:
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into the motion of charged particles inside of a magnetic field. To understand the motion, you also have to understand Magnetic fields and so I suggest you to go and read my previous posts about that first. So, without further do, let's get started!
Small recap
Until now we covered Magnetism, Magnetic fields and Gauss's law for Magnetic Flux. We saw that Magnetism has a lot of similarities with Electricity. Magnets are magnetic dipoles which are build up of a North and South that act similar to positive and negative charges. The problem is that we can't create monopoles (till now) and those monopoles don't exist in nature. This means that magnetic "charge" comes always as a pair and so the magnetic field looks similar to the electric field of a dipole with two equal but opposite charges. Magnetic field lines are closed loops and start from a north pole and terminate on a south pole. The density of the field lines shows us the actual strength of the magnetic field measured in Tesla, which sometimes is also called density of magnetix flux. The magnetic field vector is always tangent to the field lines.
The magnetic flux through a closed surface is always zero and we don't have another "non-zero" equation like in electric flux. The formula looks like this:

Magnetic fields apply magnetic forces on charged particles. The force of an electric field was parallel or anti-parallel to the motion of a charged particle and didn't depend on the velocity of that particle. Magnetic force on the other hand is orthogonal to the magnetic field vector and lines and does depend on the velocity. To determine the direction of the force we use the so called right hand rule.
Charged particle motion
Straight-line motion:
The actual motion of a charged particle depends on the perpendicular direction of his motion and the magnetic field vector. When such a charge is moving parallel to the magnetic field and so the velocity of that charge is tangent to the field lines, then the total net force is zero and the particle moves in a straight line (Newton's 1st law). You can understand it better if you think of the equation that gives us the magnetic force:

where:
- F is the force acting on a charged particle
- B is the magnetic flux density
- q uis the magnitude of charge
- v is the velocity of the charge
- θ is the angle of the velocity and magnetic field
When the magnetic field and velocity are parallel or anti-parallel then sinθ = 0, which means that there is no force.
Worth noting is that a static charged particle (stationary) experiences also no forces inside of magnetic field, because the magnetic force is proportional to the velocity. In electric fields this was not true, cause the electric force doesn't depend on the velocity of the charge.
Spiral motion:
When the velocity and force are perpendicular (θ = 90°) then the force will act either left or right to the motion/velocity of the particle and so the particle will move around in circles. The part of the velocity of a particle parallel (or anti-parallel) to the magnetic field is not affected, but the part that's perpendicular circles around it. This motion depends on the energy of the particle (charge), the velocity and the strength of the magnetic field. When a particle is moving very fast it might be deflected only a little before "leaving" the field. If the magnetic field is strong and especially if the particle loses energy, by colliding with other particle for example, then the particle might be trapped by the magnetic field. All this causes a Spiral motion.

Image source: https://commons.wikimedia.org/wiki/.../
The magnetic field "goes inside" and so the motion of the particles is perpendicular to the magnetic field. Using the right hand rule the positive charge of course "turns" left and the negative charge "turns" right, with both following a circular/spiral path.
Thinking about the work of a force we can cleary see that the magnetic field does not "work", which means that the kinetic energy and speed of the charged particle remain constant. The magnetic force is always perpendicular to the motion and so the work is: W = Fcosθ which gives us zero for θ = 90° (sin90° = 0). The magnetic force F is always perpendicular to the direction of travel and distance travelled by a charged particle. All this means that no energy is gained or lost when a particle moves through a magnetic field.
From circular motion we know that the centripedal force is:

The magnetic force provides such a force, cause it's the cause of a circular motion and so:

Solving the above equation for the radius r we have:

which shows us that the radius of the circular motion depends on the mass, velocity and charge of the particle and also on the magnetic field strength. The radius is clearly proportional to the velocity if the mass and charge remain constant.
The cyclotron frequency is given by:

The time period is T = 1/f and so:

You can clearly see that the so called Larmor frequency and period does not depend on the velocity of the particle in motion. And so when the velocity changes, what changes is the radius of the circular motion.
Helical motion:
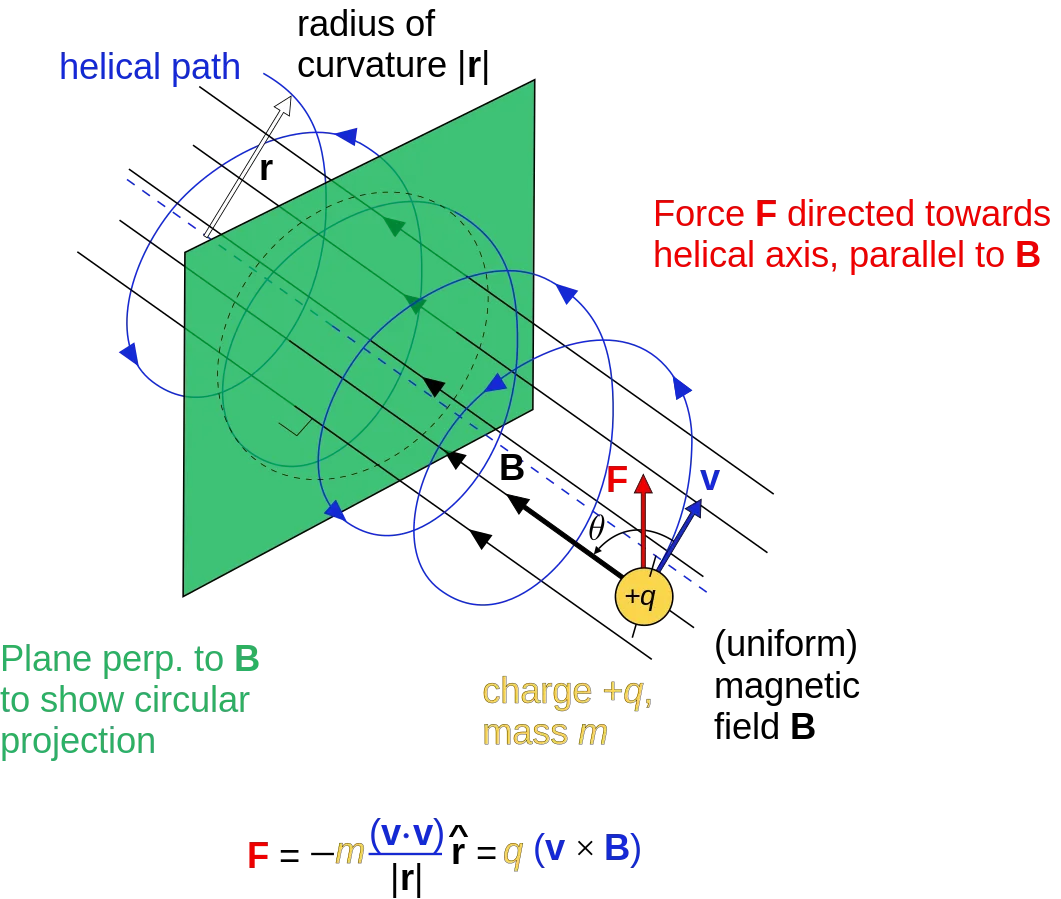
Image source: 
Last but not least we can also have a Helical motion which is the result of the velocity vector being non-perpendicular to the magnetic field vector. In this case the kinetic energy and speed of the particle remain constant, but the direction is altered by the perpendicular magnetic force. The component of the velocity parallel to the magnetic field remains unaffected and we only consider the component perpendicular to the field to make our calculations. All this means that the equation are exactly the same as with perpendicular motion, but we have to use the correct components. If the strength of the field increases in the direction of the motion that the field exerts a force to slow charges that reverses their direction. This is known as a magnetic mirror.
Sum-up:
Let's sum up what we talked about today:
- a stationary particle or particle that moves parallel to a magnetic field experiences no force and so stays at rest or keeps on moving in a straight-line motion (Newton's 1st law says hi)
- the force on charged particles acts at 90° (perpendicular) to both the field lines and direction of the particle's motion.
- magnetic force does no work and so a charge does not gain or lose energy.
- when the particle is moving perpendicular to the magnetic field then it follows a spiral path
- when the particle moves with an angle then the force is only proportional to the velocity component perpendicular to the magnetic field and so the parallel component is not affected by the field. This causes a helical motion.
- the radius of the circular "part" of the motion depends on the velocity, but the actual frequency and period only depend on the mass, charge and magnetic flux density.
REFERENCES:
- https://courses.lumenlearning.com/boundless-physics/chapter/motion-of-a-charged-particle-in-a-magnetic-field/
- http://galacticinteractions.scientopia.org/2012/02/09/charged-particles-and-magnetic-fields/
- http://farside.ph.utexas.edu/teaching/302l/lectures/node73.html
- http://www.saburchill.com/physics/chapters/0055.html
- https://www.miniphysics.com/motion-of-moving-charge-in-uniform.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism
And this is actually it for today's post and I hope that you enjoyed it!!
Next time we will get into applications of charged particle motion!
C ya!
