
Custom thumbnail that contains:
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into the Power and Wattage of Electronic Circuits. To understand this topic I highly recommend that you know a lot about current, resistance, potential and emf already. So, without further do, let's get straight into it!
Power
In physics, power is the amount of energy transferred per unit time and so the rate of work. It's a scalar quantity and calculated in J/s (SI) which is known as watt (W). Another measure of power is horsepower (hp) which is commonly used in motor vehicles. Because power is the rate of work it can be written as:

where:
- P is the power
- W the work
- t the time.
[1]
But, this is just a general definition of power, what happens in electronic circuits?
Wattage
Electric power is the rate at which electrical energy is transferred by an electronic circuit. The SI unit is of course the same as before and so 1 J/s = 1 watt. Another term for electric power is: Wattage, which means "electric power in watts".
[2]
Let's consider the following diagram:
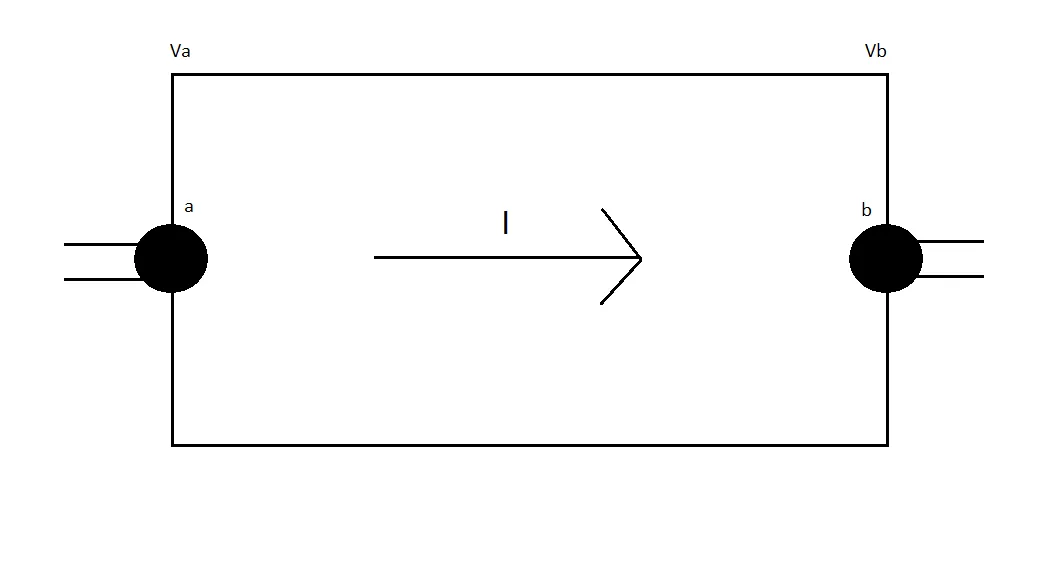
There is potential difference Vab = Va - Vb between the terminals a and b, and an electric current I flows from a to b. The total work produced to each charge q of the current is equal to q*Vab (cause potential is equal to W/q as we know from previous posts). Supposing that Vab is positive then the work of the electric force is +qVa, cause we go from the higher potential Va to the lower potential Vb. With current I and in time dt the total charge "passing" is dQ = Idt (from the definition of current). The work that is produced to this charge is:

This work of course represents the energy that is transferred to the unit of the circuit. The actual rate in which this energy is transferred is the power that we discussed a minute ago. And so the power of an electronic circuit is given by:

If the unit we are referring to is a resistor with resistance R then because of Ohm's law the power can be calculated with 3 equivalent equations:
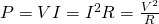
where:
- V is the potential difference or Voltage across the resistor (in Volts)
- I is the electric current flowign through the resistor (in Amperes)
- R is the resistance of the resistor (in Ohm's)
Of course the voltage must be greater then zero, which means that the potential a is greater then the potential of b and so we have a voltage-drop that closely relates to the power.
[3]
But, what is this energy that gets produced and used up? Well the energy of course is heat dissipation. Resistors reduce the current in circuits and protect it from overdrawing by dissipating the kinetic energy of the moving electrons in current as thermal energy or heat. The actual origin of this power dissipation are the inelastic collisions of the conducting electrons with the molecules of the conductive material.
[4]
Lastly, let's also relate all this with the EMF! In the previous post we said that the voltage or potential difference between to points a and b of a EMF component is:

where:
- ε is the EMF or electromotive force
- I the electric current
- r the internal resistance of the EMF
We know that the power is given by the equation P = VI and so let's multiply the upper equation with I to get the power of the EMF energy supply unit...

where:
- "εI" is the rate in which work is produced to the charges moving and so represents the ratio in which the non-electric energy stored in the battery is converted to electric energy inside of the source.
- "I^2r" is the ratio in which energy is dissipated by the internal resistance r of the EMF.
That way the whole equation gives us the actual power output of the source and so the ratio in which the energy source supplies electrical energy to the rest of the circuit.
Another cool way of proving this equation is explained in the following article:
Electromotive Force and Power in Circuits
REFERENCES:
- https://en.wikipedia.org/wiki/Power_(physics)
- https://en.wikipedia.org/wiki/Electric_power
- https://www.electronics-tutorials.ws/resistor/res_7.html
- https://brilliant.org/wiki/heat-dissipated-by-resistors/
All the mathematical equations that I had in this post where drawn using quicklatex to make them look better!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
And this is actually it for today's post!
Next time I will either explain the conductivity of materials or get into electric current exercises and leave the other post for later...
Bye!
