Image source: https://www.physicsforums.com/threads/understanding-motional-emf.753716/
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Motional Electromotive Force (Emf) that we introduced a little bit last time. There is a lot to say around this topic and so I decided to make a separate article about it :) So, without further do, let's get started with today's post!
Quick Recap
Electromagnetic Induction only occurs and can be observed when a magnet is moving relative to a electrical conductor. The sign/direction of the induced voltage depends on the direction of the motion and orientation of the magnet (the magnetic flux changes depending on the motion and orientation). The magnitude only depends on the voltage only depends on the speed of the magnet's motion. The induced voltage increases when increasing the number of coils. All these behaviours where described by Faraday in his law (Faraday's law) that stated:
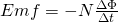
where:
- N is the number of coils
- Φ the magnetic flux (change by time)
- Emf the electromotive force / induced voltage
Motional Emf
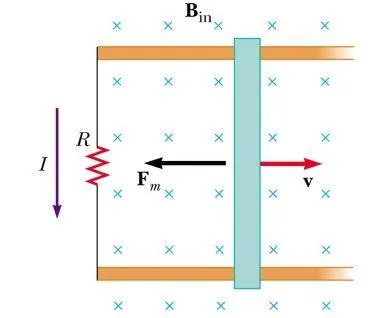
As we have seen until now, motion is one of the major causes of induction. Induced voltage or Electromotive Force (emf) can be produced by moving a magnet towards a coil or a coil towards a magnet, something that produces a similar emf. Motional Emf is a term that is used for moving objects in stationary magnetic fields. In previous articles we already said that charges moving in a magnetic field experience a magnetic force that is described by the equation:

where:
- q is the magnitude of charge
- v is the velocity of the motion
- B the magnetic field strength
This force moves opposite charges in opposite directions and has a direction that can be found by the right-hand rule (for positive charges).
The magnetic force and field are binded by the equation:
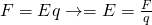
For bars of length L that are within an electric field E we proved in previous articles that:
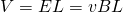
where E = vB (substitution).
For all these calculations we of course considered a uniform magnetic field B all over the length of the bar. The separation of charge in the bar creates an electric field within the bar in the downward direction, since the top of the bar is positively charged and the bottom of the bar is negatively charged. The electric force pulls negative charges upwards, while the magnetic force pulls negative charges downward. Magnetic fields are initially stronger then electric fields and so more electrons are drawn to the bottom and so the electric field becomes increasingly stronger. From all this we can see that the direction of the induced voltage / emf produced is opposite, something that explains the negative sign that we had in the previous article. (More about the direction will be discussed next time with Lenz's law)
To summarize really quick, when a moving bar is a source of electromotive force, this emf is called motional emf and defined as:
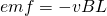
where:
- v is the speed of the bar's motion
- B the magnetic field's magnitude/strength
- L the length of the bar
v, B and L need to be mutually perpendicular.
The magnitude of the induced emf can be increased by increasing the strength of the magnetic field, moving the bar faster, or using a longer bar.
A great example is the measurable potential difference between the wingtips of airplanes. The Earth's field is relatively weak, but the high velocity and substanctial length induce a reasonable motional emf!
Faraday's law and motional emf
For loops of wire moving with a velocity v into stationary magnetic fields, Faraday's law is described as:
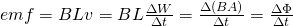
Where the left part is the special case that only applies for bar's of length L and uniform magnetic fields. The far-right equation is the more general case and the law that we described last time..
Generalization
For any two points A and B the motional emf is:
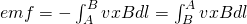
where:
- v is the velocity of the conductor
- B any magnetic field
- dl is a infinitesimal length
This integral build up of infinitesimal emf's that are calculated through:
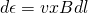
Note that the magnetic field can be uniform or not. Also vxB is a cross product between vectors that can be replaced by vBsinθ, which gives us just a magnitude, if a "numeral" value is what we need. The direction of anything can be calculated in many different ways and so changing the equation into:

might sometimes be of great use!
REFERENCES:
- https://em.geosci.xyz/content/maxwell1_fundamentals/formative_laws/faraday.html
- https://courses.lumenlearning.com/physics/chapter/23-3-motional-emf/
- http://www.sparknotes.com/testprep/books/sat2/physics/chapter16section1.rhtml
- https://opentextbc.ca/physicstestbook2/chapter/motional-emf/
- http://physics.bu.edu/~duffy/sc545_notes02/motional_emf.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elevol.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism
The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion
Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens
Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs
Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque
Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them
Magnetic field exercises -> examples in magnetic force, magnetic flux, particle motion and forces/torque on current-carrying conductors
Magnetic field sources:
Magnetic field of a moving charged particle -> moving charge, magnetic field, force between parallel charged particles
Magnetic field of current-carrying conductors -> magnetic field of current, Biot-Savart law
Force between parallel conductors and the magnetic field of a current loop-> force between parallel conductors, magnetic field of current loop
Ampere's law and Applications -> Ampere's law, applications
Magnetic materials -> Magnetic materials, classification and types, material examples
Displacement current -> Displacement current, Extension of Ampere's law
Exercises in Magnetic field sources -> examples all around magnetic field sources
Electromagnetic Induction:
Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law
And this is actually it for today's post! Next time in Physics we will get into Lenz's law and Induced Electric Fields...
Bye!
