Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into Millikan's Oil Drop Experiment!
During the proof we will use a lot of concepts, equations etc. that we covered throughout the series, but also stuff that we didn't. Don't worry, I will explain why wo do each step either way! :)
So, without further do, let's dive straight into it!
What this experiment is all about
During some of my first posts of Electromagnetism I told you about charge quantization. Which means that any charge is the multiple of some elementary charge.
This elementary charge is denoted as e or q and describes the charge of a single proton or the magnitude of charge of an single electron (which is -e). And so to avoid the sign we mostly use the term: elementary positive charge.[2]
Always remember that protons and electrons are equal and oppositely charged!
Knowing that electrons are easier "to move around" scientists tried different experiments to find out the value of this charge!
The oil drop experiment was performed by Robert A. Millikan and Harvey Flether to measure the charge of the electron. The procedure involved observing tiny electrically charged droplets of oil located between two parallel metal surfaces that form the plates of an capacitor. The plates were oriented horizontally. [1]
This experiment was the first that succeeded and a very difficult experimental problem, cause determining a precise value for the electric charge of an electron e is indeed not that easy. The unit of electric charge is of course an fundamental physical constant and crucial for calculations within electromagnetism and so Millikan was recognised with a Nobel price of physics! [3]
The Apparatus/Design used
The design of Millikan's oil drop apparatus was simple, but an powerful tool to determine the charge of the "dropped" oil particle. [4]
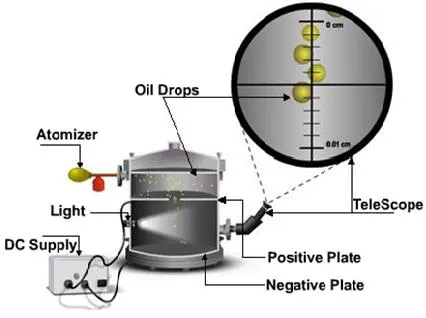
The figure below shows the apparatus:
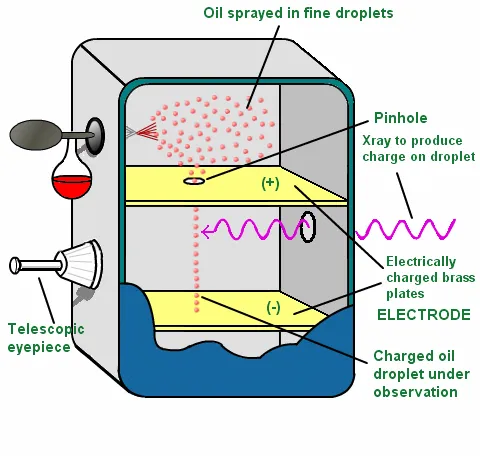
As you can see from the figure, there are two chambers:
- the above chamber is used for spraying tiny droplets of oil
- the second chamber was empty space separated by electrodes (the two parallel plates)
Of course the potential difference between the electrodes is high so that the droplet doesn't free fall when subject to the electric field.
An x ray was used to charge the oil drop, by "giving away" it's charge to the oil drop. Being charged the oil drop of course starts dropping, cause it's influenced by the uniform electric field, but it's stops midway and so calculating the charge of the oil drop using the known electric field and other parameters becomes very easy! [4]
Theory and procedure
We know the electric field and have a charged oil drop falling or rising (depending on the charge), but how do we end up with the charge of an electron or even the actual charge of this particle?
This means that the experiment resolves around the actual motion of those droplets. To understand this motion we of course have to find out which forces act on the oil drops. [3]
We of course don't have Weight (gravity) and Electrical force only, but also Buoyancy and Drag forces to make the calculations more precise.
So, now there are two senarios:

On the left the droplet is falling through the air and on the right the droplet is rising due to an applied electric field (which means that the charge needs to be negative).
Let's first get into an easy "proof"... (from [4])
The weight is of course F = mg, where m is the mass of the droplet and g the gravity of the earth.
The electrical force is F = qE, where q is the charge of the droplet and E the electric field.
Equating these two (point where the charge stops midway) we get:
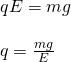
Let's now get into the more "advanced" proof... (from [3])
The gravitational pull applied to the droplet is:
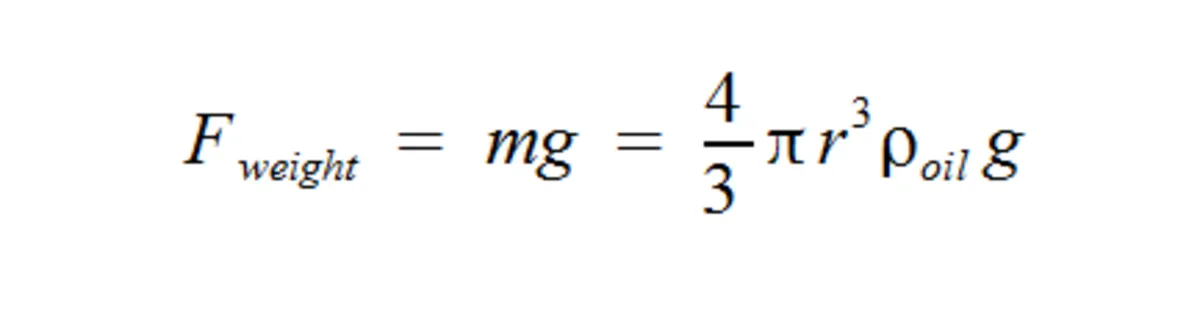
The buoyancy force is:
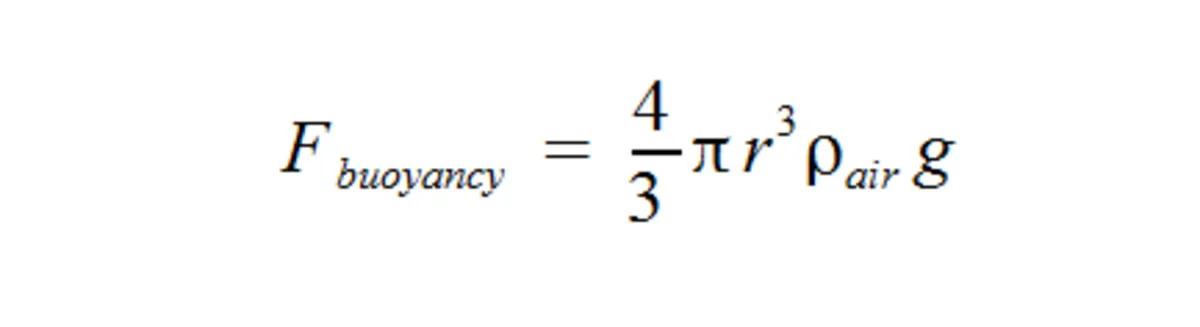
The drag force using Stoke's law is:

The only thing unknown is the radius of the droplet for all the equations...
Without an electric field we reach the terminal velocity for falling when:
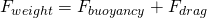
Which gives as the radius of the droplet:

When an strong enough electric field is applied that is able to make the droplet rise with a force F = qE that is heading upwards then the charge will of get to the terminal velocity of rising when:
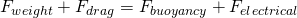
The only thing unknown now is the charge and so the charge of the particle is:

where:
- d is the distance of the electrodes
- v1 the terminal velocity of falling
- v2 the terminal velocity of rising
- V the voltage/potential between the two plates
- p the densities of oil and air
By using the equation that gives us the radius r and by putting this radius into the "simple" equation q = mg/E we get a result that doesn't contain the terminal velocity of rising!
Which means that it's much easier to calculate the charge by using:

where the velocity v is the terminal velocity of falling.
That way we can "let" the drop fall down, which helps us calculate the terminal velocity v and because the rest is known we can directly find the charge q. Cool?
Using this technique Millikan calculated the charge of an electron equal to:
e = -1.5924 x 10^-19C
which is very close to the accepted value of today which is approximately:
e = -1.602 x 10^-19C
where the '-' is not being used most of the times!
Electronvolt
An electronvolt (eV) is a unit of energy equal to e (elementary charge) J (Joules).
By definition it is the amount of energy gained or lost by the charge of a single electron moving across an electric potential difference of 1V. [5]
And so eV = 1 volt(J/C) * e (elementary charge or charge of an single electron in C).
We use the multiples meV, keV, MeV etc. of it in a lot of calculations!
The electronvolt is used a lot in other branches of Physics that are about particles, molecules etc. and so talk about the smaller things in nature and where the smallest charge and a metric of calculating the energy given or taken by such a small particle plays a very big role!
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
REFERENCES:
https://en.wikipedia.org/wiki/Oil_drop_experiment [1]
https://en.wikipedia.org/wiki/Elementary_charge [2]
https://owlcation.com/stem/Millikans-Oil-Drop-Experiment [3]
https://physics.tutorvista.com/modern-physics/millikan-oil-drop.html [4]
https://en.wikipedia.org/wiki/Electronvolt [5]
And this is actually it for today!
Next time we will explain how Cathode ray tubes work using electric potential!
Bye!
