
Image source: https://upload.wikimedia.org/wikipedia/.../
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Magnetic fields. What we covered 'till now was mostly the "Electricity" part of Electromagnetism. With this post we finally get into Magnetism too. The two main things that I will cover is what Magnetism is and we will also get into Magnetic fields. So, without further do, let's get straight into it!
Magnetic field lines
As we already told last time, the magnetic field (sometimes also called B-field) describes the influence of magnetic forces in a region. The same way as an electric field described the electric forces applied in a specific region. To represent such a magnetic field we use magnetic field lines which describe the direction of the magnetic force on a north monopole at any given position. Remember what we said last time? The direction of the magnetic field lines is north to south pole, which means that the lines emerge out of north poles and enter south poles. Of course monopoles don't exist in nature (or do they?), but definining the concept helps us connect magnetic monopoles with electric charges that are either positive, negative or neutral charged. Theoretically, the magnetic field's strength can be calculated at every position in space, but because it's very hard to visualize that, the densitiy of the field lines indicates the actual field strength at every point and so points far away (infinite distance) get "zero" force applied. The direction of the magnetic field is tangent to the field line at any point.
Magnetic monopoles
So, what is a magnetic monopole? It's a theoretical object that has either a north or a south pole. Thing about them as magnetic charges similar to positively charged protons and negatively charged electrons. They of course don't exist, but we might be able to artificially synthesize them. Either way, they are very useful, cuse they help us reduce magnetic phenomena to their electrostatic analogue. If they could be isolated in nature, they would exhibit the same behavior as electric charges by creating a "radial" magnetic field around them.

Image source:
Something worth noting is that we can't just "break" a dipole magnet in half, cause then we would just create two dipoles out of it, exactly as the following image is describing:

Image Source: 
It is impossible to separate the North and South poles of a bar magnet. When breaking the magnet in two you get two magnets, where both will have a North and South pole. Even after reaching atomic level, elementary particles still behave like magnetic dipoles and so it appears that in nature magnetic monopoles cannot be created. However, quantum theories like the "theory of everything" note that magnetic monopoles where created as elementary particles after the birth of the Universe. After the creation the magnetic monopoles interactions with the rest of the matter where highly suppressed. But, still physists search for evidence for the existence of magnetic monopoles.
Real or not magnetic monopoles (or charges) should follow a Coulomb-like law in the form:

Magnetic dipoles
The combination of two magnetic monopoles labeled North and South is called a magnetic dipole. This is of course very similar to the electric dipole that is build up of two equal but opposite electric charges +q and -q. The simplest form of such a magnetic dipole is the so called bar magnet. The magnetic field of such a magnet looks like this:

Image source: 
You can see that the magnetic field lines are very dense when being close to the magnetic poles of the magnet. This reflects the high field strength near the poles. At other points the field lines become less dense meaning diminished field strength. In this picutre you can now also tsee that field lines begin at the north pole and terminate at the south pole. Magnetic field lines (the same way as electric field lines) cannot intersect each other (cross), because they represent the trajectory of particles. The are drawn as parallel trajectories.
Superposition principle
When having more magnets and so more magnetic fields the so called superposition principle, that we also talked about in electric fields, comes into play. This principle tells us that the magnetic field strength at any point is equal to the vector addition of all the magnetic field lines (which are also vectors) at that point. So, what does this mean? Well, when calculating the total magnetic force or magnetic field applied at a point we can calculate each separate magnetic field's influence by ignoring the other potential field generating objects. After doing that we just have to vector sum all of them together. So, when two or more magnetic fields act on a point x the total magnetic field is:
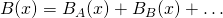
The properties of magnetic field lines can be summarized as:
- The direction of the magnetic field is tangent to the field line at any point
- The strength of the field is proportional to the density of the lines.
- Field lines never intersect each other.
- Field lines are continuous and form closed loops starting from a north to a south pole.
Magnetic Flux
The same way as we had electric flux we also have magnetic flux. Magnetic flux measures the total magnetic field passing through a given area. It's useful for describing the effects of magnetic force on something that occupies a given area A. Of course the magnetic flux is tied to the area chosen. We are free to choose an area of any size and orientation relative to the magnetic field. Thinking about the field-line representation each field line passing through an area of course contributes to the total magnetic flux. The same way as with electric flux, magnetic flux only includes the components of the magnetic field vector which are normal to our test area.
Let's say that we have a simple flat surface of area A with an angle θ between the normal to the surface and the magnetic field vector B. The magnetic flux is given by:

When the angle is zero the magnitude of the magnetic flux is simply BA.
The SI unit of magnetic flux is the Weber, which is noted as Wb. 1 Wb is of course equal to 1 T m^2. Using a magnetometer we can measure the magnetic flux, the same we as we measure magnetic fields, because flux is just another way of expressing magnetic fields. Another interesting term is the so called magnetic flux density which is measured in Wb/m^2. By dividing flux by area we of coures end up with the magnetic field magnitude measured in Tesla. And so 1 T = 1 Wb/m^2, which is why magnetic field strength or magnitude is sometimes also called magnetic flux density.
Gauss's law of Magnetism
When we got into Electric flux we talked about Gauss's law. The electric flux inside of a charge distribution was always zero and calculating the total flux outside could be done easily using the Gauss integral. Gauss's law also applies in magnetism and magnetic fields. Gauss's law states that no monopoles exist and that the total magnetic flux through a closed surface must be zero. Gauss's law for magnetic fields in area integral form is given by:

where:
- B is the magnetic field strength or flux density
- S the arbitrary closed surface, which is sometimes called Gaussian surface
By saying that this equals zero it's like saying that the number of magnetic field lines that enter and exit through this closed surface S is the same. This means that the strength of the south is equal to the strength of the north pole and monopoles don't exist, cause then there has to be an equal amount of the "other" pole. For every "positive" magnetic pole there has to be an equal amount of "negative" magnetic poles.
Gauss's law can also be described by a differential equation, which in the end gives us:
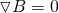
and so the Del or derivative along B must be zero.
Note that Gauss's law doesn't have a "non-zero" form in magnetism, like the one that we had for electricity where the flux equaled the total charge divided by ε0. "Magnet charges" and so north and south poles always exist in pairsm which means that the "magnetic charge" is always zero. Also, don't forget that we are talking about closed surfaces. When talking about generally not closed surfaces we get into Faraday's law, which is a law that we will cover later on in this series.
REFERENCES:
- https://brilliant.org/wiki/magnetic-field-lines/
- http://www.physics.louisville.edu/cldavis/phys299/notes/mag_monopoles.html
- https://opentextbc.ca/physicstestbook2/chapter/magnetic-fields-and-magnetic-field-lines/
- https://www.khanacademy.org/science/physics/magnetic-forces-and-magnetic-fields/magnetic-flux-faradays-law/a/what-is-magnetic-flux
- https://em.geosci.xyz/content/maxwell1_fundamentals/formative_laws/gauss_magnetic.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/fluxmg.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/electric/maxeq2.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications
Electrical measuring instruments -> what are they?, types list, getting into some of them, an application
Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply
RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance
Magnetic field and forces:
Magnetic fields -> Magnetism, Magnetic field
And this is actually it for today's post and I hope that you enjoyed it!!
Next time we will get into the motion of charged particles inside of a magnetic field!
Bye!
