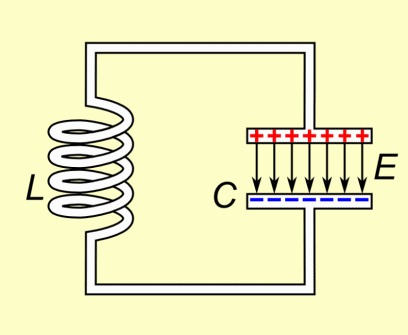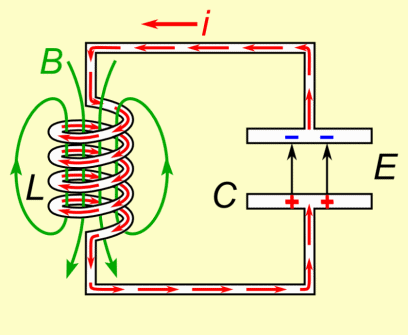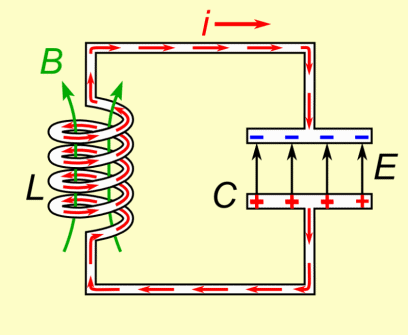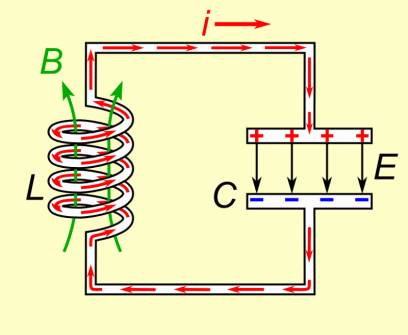
Physics - Electromagnetism - Magnetic Energy Density

Image source: https://brilliant.org/wiki/energy-of-a-magnetic-field/

Introduction

Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Magnetic Energy Density. So, without further do, let's get straight into it!

Energy stored in a magnetic field (or inductor)

When conductors carry current, a magnetic field surrounding them is being produced. Having the current change with time we cause an electromagnetic induction, which causes the creation of a electromotive force (emf), that is a voltage that opposes the change in magnetic flux (Lenz's law) that was created by the change of current (magnetic flux is proportional to the current). As we already saw in the previous posts there is one "main" type of induction, which is the so called Mutual Induction between two conductors. One of them is the causes a mutual induction on the other and sometimes the "other" conductor may even be itself (self-induction).

The creation of such a opposing voltage (emf) must have some origin (it cannot be created from nothing). Due to energy convervation, some energy needs to drive the original current. This energy can be thought as some form of potential energy that would be imparted on charged particles moving through a region with a magnetic field present.

By definition, the magnetic energy (potenial energy) stored inside of an inductor is equal to:

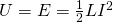
Where:

E or U is the magnetic/potential energy stored in a inductor
L the inductance of the inductor
I the current flowing through it

Let's now consider a solenoid with length l, N number of turns, cross-section area A and current I that of course works as an inductor. Let's replace the inductance L with the corresponding equation we talked about last time. That way we end up with the following equation for the magnetic energy stored in a solenoid:

Magnetic Energy Density

From the previous equation we get that the energy density, which is calculated as energy/volume is given by the equation:

where:

B is the magnetic field strength
μ mostly the constant μ0 (permeability of free space)

For a electromagnetic wave which has a electric / magnetic field ratio c (speed of light) we can also write the electric field's energy density as:

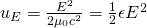
where:

ε is mostly the vacuum pemittivity constant ε0 = 1 / μ0c^2 (as we know from previously)
E the electric field magnitude/strength

We can clearly see that both the electric and magnetic fields transport energy, when talking about electromagnetic waves!

Coaxial Cable Inductance Example

Consider two concentric cylindrical shell of radius R1 and R2 respectivelly. Let's determine the magnetic energy stored per unit of length and also the self-inductance per unit of length of cable.

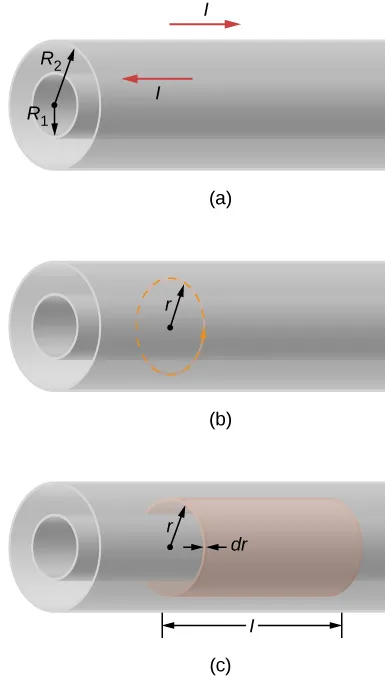
Image source: https://phys.libretexts.org/.../

Using Ampere's law the calculation of the magnetic field both inside and outside of the coaxial cable is very easy! Based on this magnetic field B we can then calculate the energy density of the magnetic field, which now will needs to be an integral over the entire volume of the cylindrical shell. After that the self-inductance per unit length is very easy to calculate! So, let's start!

Using the dashed circular path of figure (b) and because of cylindrical symmtery, considering that B is constant along the path we have:

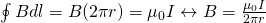
No current is flowing outside of the cable and so B = 0 for any circular path with r > R2 (outside of both cylinders) or r < R1 (inside of the "inside" cylinder). Therefore, all the magnetic energy of the cable must be stored in between of the two conductors.

The energy density of the magnetic field is:

which is stored in a cylindrical shell of inner radius r and outer radius r +dr, and with a length l as shown in figure (c).

By integrating the energy density for this region we get:

Dividing the result with l we get the energy per unit length which is:

From the simple equation of U we calculate the self-inductance per unit length as:

Note that the indutance per unit length only depends on the inner and outer radius of the cable. This means that we can increase it by increasing R2 or decreasing R1, which can also be done by "changing" these cables. Again a physical/geometrical constant...in some way

REFERENCES:

Mathematical equations that I had in this post where drawn using quicklatex!

Previous posts about Electromagnetism

Electric fields:

Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization

Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples

Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines

Electric dipoles -> Electric dipole, torque, potential and field

Electric charge and field Exercises -> examples in electric charges and fields

Electric flux:

Electric flux and Gauss's law -> Electric flux, Gauss's law

Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications

Applications of Gauss's law (part 2) -> more Gauss applications

Electric flux exercises -> examples in electric flux and Gauss's law

Electric potential:

Electric potential energy -> explanation of work-energy, electric potential energy

Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials

Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient

Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt

Cathode ray tubes explained using electric potential -> cathode ray tube explanation

Electric potential exercises (part 1) -> applications of potential

Electric potential exercises (part 2) -> applications of potential gradient, advanced examples

Capacitance:

Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance

How to solve problems around Capacitors -> combination, solving problems, simple example

Electric field energy and density -> Electric field energy, energy density

Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems

Electric capacitance exercises -> examples in capacitance, energy density and dielectrics

Current, resistance and EMF:

Electric current -> Electric current, current density

Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity

Electric resistance -> Resistance, temperature, resistors

Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance

Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits

Electric current, resistance and emf exercises -> exampes in all those topics

Direct current (DC) circuits:

Resistor Combinations -> Resistor combinations, how to solve problems

Kirchhoff's laws with applications -> Kirchhoff's laws, how to solve problems, applications

Electrical measuring instruments -> what are they?, types list, getting into some of them, an application

Electronic circuits with resistors and capacitors (R-C) -> R-C Circuit, charging, time constant, discharging, how to apply

RC circuit exercises -> examples in Kirchhoff, charging, discharging capacitor with/without internal resistance

Magnetic field and forces:

Magnetic fields -> Magnetism, Magnetic field

Magnetic field lines and Gauss's law of Magnetism -> magnetic field lines, mono- and dipoles, Flux, Gauss's law of magnetism

The motion of charged particles inside of a magnetic field -> straight-line, spiral and helical particle motion

Applications of charged particle motion -> CERN, Cyclotrons, Synchrotrons, Cavity Magetron, Mass Spectrometry and Magnetic lens

Magnetic force applied on Current-Carrying Conductors -> magnetic force on current-carrying conductors/wires, proofs

Magnetic force and torque applied on current loops (circuits) -> magnetic force on current loops, magnetic moment and torque

Explaining the Physics behind Electromotors -> tesla, history and explaining the physics behind them

Magnetic field exercises -> examples in magnetic force, magnetic flux, particle motion and forces/torque on current-carrying conductors

Magnetic field sources:

Magnetic field of a moving charged particle -> moving charge, magnetic field, force between parallel charged particles

Magnetic field of current-carrying conductors -> magnetic field of current, Biot-Savart law

Force between parallel conductors and the magnetic field of a current loop-> force between parallel conductors, magnetic field of current loop

Ampere's law and Applications -> Ampere's law, applications

Magnetic materials -> Magnetic materials, classification and types, material examples

Displacement current -> Displacement current, Extension of Ampere's law

Exercises in Magnetic field sources -> examples all around magnetic field sources

Electromagnetic Induction:

Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law

Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization

Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields

Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)

Maxwell's equations -> What they are, each equation analyzed separately

Electromagnetic Induction exercises -> examples all around Electromagnetic Induction

Mutual and Self Induction:

Mutual Inductance -> Mutual Inductance, applications

Self Induction -> Self Induction, Lenz's law, Inductance of a Coil

And this is actually it for today's post and I hope that you enjoyed it! Next time in Physics we will get into R-L (resistor-inductor) circuits.

Bye!