
Image source: https://en.wikipedia.org
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into how we solve more "complex" circuits that can't be solved using Ohm's law and simple resistor combinations. To solve such advanced circuits we use Kirchhoff's laws that give us rules about the electric current and voltage (potential difference) of electronic circuits. Of course checking out previous posts will be helpful and so I suggest you to know everything from the: Current, resistance and EMF "part" of this series. So, without further do, let's get straight into it!
Kirchhoff's laws
When having resistors in series, parallel or combinations of the previous two the single total/equivalent resistance can be found very easily, because we can apply Ohm's law. But in more complex circuits that are not composed exclusively of such combinations we can't apply Ohm's law and so get into the more powerful relation described by Kirchhoffs Circuit Laws. The pair of rules describes the conservation of energy and charge in electrical networks, where one deals with the current flowing around a closed circuit (KCL), while the other one talks about the voltage sources in a closed circuit (KVL).
Let's get into each law on it's own.
Current Law (KCL)
The first law is all about the current leaving and entering a node and states that:

which means that "the total current or charge entering a junction or node is equal to the charge leaving the node, cause the charge has no other place to go except to leave as no charge is lost within the node (conservation of charge)". That's why the sum of all the currents leaving a node in always equal to zero.
We sometimes also use it like that:

which is an equation that shows us the "actual law".
But, you might ask yourself what do you mean with junction or node? From Graph theory we know that a network is build up of nodes and edges. The dots are nodes and the lines are edges and so the dots indicate the connection-point between those lines. The lines are connections and can also be thinked of as wires that are ideal and have zero resistance. Lastly, don't forget that we don't use dots if the connection is obvious and that we sometimes might have 2 or more dots that represent the same node. So, a Junction is a point where 2 or more circuit components (or current carrying paths) are connected to each other.
Voltage Law (KVL)
The second law is about the voltage drops and rises over a closed loop and states that:

which means that "the total voltage around a loop (which is zero) is equal to the sum of all the voltage drops within the same loop". And so the algebraic sum of all the potential differences across all the elements within a closed loop in any network must be equal to zero. This law of course is a result of energy conversation, cause any charge that starts and ends up at the same point with the same physical condition must have the same energy afterwards and so should have gained as much energy as it lost.
How to solve problems
So, how do we apply those laws?
- When applying the KCL law we consider the currents leaving being positive and the currents entering being negative in sign (that's why we can also use the sum of all currents being equal to zero).
- When applying KVL we start from a point in the loop and maintain the same clockwise or anti-clockwise direction, noting all the voltage drops as negative and rises as positive so that the final sum is zero. (What we tend to do is setting the voltage of the battery or energy supply equal to the sum of the voltage drops of all the resistors in the loop)
Sign conventions:
- EMF (ε) is noted positive in a loop from - to + and negative in a loop from + to -.
- The voltage drop (IR) is noted negative if our "looping" direction is the same as the assumed current direction through the resitor. It's positive if it's opposite.
- An "increase" of potential difference is always positive and a "decrease" always negative.
An actual step guide is the following:
- Draw the circuit and assign labels to the known and unknown quantities. For currents specifically, you also have to assign directions. If you guess incorrectly then the curnet will come out as negative, but with the correct magnitude/value.
- Select the independent variable. We have to choose either the voltage or current and will of course choose the one that has the "smallest" number of unknown variables and so will give us less terms in our equations.
- Apply the junction rule (KCL) to the junctions and the loop rule (KVL) to the loops that contain the independent variables that you declared in the previous step. You should end up with n independent equations for n independent variables, where each element is represented in at least one equation. In general there will be more loops present thatn "needed" to solve for all the unknowns and so we use those for consistency checking.
- Solve the system of independent variables (voltages or currents).
- Solve for the other unknows using Ohm's law, which means that if we calculated the voltages using the system than we can find the currents using i = v/R and vise versa.
Because we have to solve a linear system you have to know some Linear algebra that I covered in my blog quite some time ago and that you can find in my recap!
Applications
1.
A loop circuit, where only KVL is needed...
Consider the schema:

where we have 2 batteries and 2 resistors connected in a closed loop circuit with:
- r1 = 2Ω, V1 = 12V
- r2 = 4Ω, V2 = 4V
- R1 = 3Ω, R2 = 7 Ω
The unknown variables are the voltage Vab and current I.
Solution:
There is only one current and so one branch/loop in the circuit which means that KCL is unnecessary. The only thing that we have to apply is KVL. I already assumed a direction for the current in my diagram and let's say that we also follow this direction for applying KVL.
KVL:
Starting of at the point A we do the following:
- The assumed current goes in the same direction that we "loop around" and so the voltage drop at the internal resistor r2 is "negative" and equal to -I*r2 = -I(4Ω).
- We go through the emf of 4V in the order + to - which means that we have to take it as negative (-4V).
- The resistor R2 is again passed with a current in the same direction and so we substract the voltage drop which is equal to -I*R2 = -I(7Ω)
- We go through the emf of 12V in the direciton - t0 + which means that we have a voltage increase and so we take it as postive (12V).
- For the same reasons as before the internal resistor r1 gives us a voltage drop of -I*r1 = -I(2Ω)
- And the same for the resistor R1 which gives us a voltage drop of -I*R1 = -I(3Ω)
That way we end up with the equation:

The only unknown variable is I and so solving for it we get:

Note that the current is positive which means that our assumption was correct. If it was negative (I = -0.5A) then we would have to change the current's direction in our schema.
To calculate the voltage Vab we have to start from point B and go to A by adding the voltage changes in the way. There are of course two ways: the "top" and "bottom". In the "top" one we follow the current's direction and so the voltage drops at the resistors will be negative and the emf "voltage increase" will be positive. In the "bottom" one we follow the opposite direction and so the voltage drops and the emf will all be positive!
The "top" one gives us:

The "bottom" one gives us:
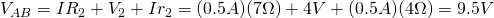
You can see that both are giving us the same result!
2.
Based (somewhat) on Example 1 from http://www.resistorguide.com/kirchhoff-law/ but with actual values...
Consider the schema:

From http://electricalengineeringforbeginners.blogspot.com
There are no given parameters and so let's just give some ourselfs!
Let's consider:
- E1 or V1 being a battery of 13V with no internal resistance.
- The resistors have resistances R1 = R2 = R3 = R4 = 1Ω and R5 = 2Ω
What we want to calculate is:
- the single equivalent resistance R
- the current that flows through all the components
To find these let's assume the following current directions and loops:

By applying the KCL rule we have that:
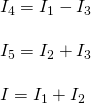
And so 3 are the unknown currents, which of course means that current will be our independent variable.
Let's now also apply the KVL rule for each of the three loops...
Loop 1:
- We go through the battery in the order - to + which means that we take it positive (+13V)
- At each of the 2 resistors in the loop the current goes in the same direction as our "loop-direction" and so the voltage drop is negative for both [-I1*R1 and -(I1-I3)R4]
That way the equation is:

Loop 2:
- The two resistances will give us "negative" voltage drops [-I2R2 and -(I2+I3)R5]
- We again pass through the EMF in the order - to + and so have a positive term (+13V)
So, the equation is:

Loop 3:
- We go through resistor R1 in the same direction as the current and so have a "negative" voltage drop (-I1R1)
- The same happens for R3 (-I3R3)
- For R2 on the other hand we have the opposite direction and so their is a voltage "increase" (+I2R2)
This gives us the equation:

And so we end up with the linear system:

This system can be solved in many ways, but an easy way is by solving the last equation for I2: I2 = I1 + I3 and by substituting this in the second equation. By doing so we end up with the system:

By multiplying the first one with 5 and addition we end up with:

By putting this calculated value in the first equation we get I3 as:

Ooops, we have a negative sign! This means that the current is going in the other direction!
From the 3rd and final equation we also calculate I2 as:

After doing all this we are now able to calculate all the currents:

Note that we keep that "wrong" direction for I3, but you could also change it and calculate the new KCL equations for I4 and I5 with the correct direction.
The total resistance of the circuit is of course given by Ohm's law and is:
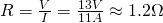
Another great and full solution can be found here.
Note that what we proved last time for resistor combinations and the EMF can be proved using Kirchhoff's laws very easily. I found a very good explanation here in the 3rd section.
REFERENCES:
- https://www.electronics-tutorials.ws/dccircuits/dcp_4.html
- https://www.khanacademy.org/science/electrical-engineering/ee-circuit-analysis-topic/circuit-elements/a/ee-circuit-terminology
- https://www.khanacademy.org/science/physics/circuits-topic/circuits-resistance/a/ee-kirchhoffs-laws
- https://www.khanacademy.org/science/electrical-engineering/ee-circuit-analysis-topic/ee-dc-circuit-analysis/a/ee-application-of-the-fundamental-laws
- http://theory.uwinnipeg.ca/physics/curr/node8.html
- http://www.resistorguide.com/kirchhoff-law/
Mathematical equations that I had in this post where drawn using quicklatex!
Previous posts about Electromagnetism
Electric fields:
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux:
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential:
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitance:
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Current, resistance and EMF:
Electric current -> Electric current, current density
Electrical resistivity and conductivity -> Electrical resistivity, conductivity, thermal coefficient of resistivity, hyperconductivity
Electric resistance -> Resistance, temperature, resistors
Electromotive Force (EMF) and Internal resistance -> Electromotive force, internal resistance
Power and Wattage of Electronic Circuits -> Power in general, power/wattage of electronic circuits
Electric current, resistance and emf exercises -> exampes in all those topics
Direct current (DC) circuits:
Resistor Combinations -> Resistor combinations, how to solve problems
And this is actually it for today's post!
Next time I'm thinking of covering the different measuring instruments that we have for electronic circuit units/metrics!
Bye bye!
