Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into Electrical resistivity and conductivity!
All the mathematical equations will be drawn using quicklatex!
So, without further do, let's get straight into it!
Electrical resistivity of materials
First of all Electrical resistivity that we will talk about should NOT be confused with electric resistance that we will talk about next time!! (but they actually are the same thing, but covered from another respective)
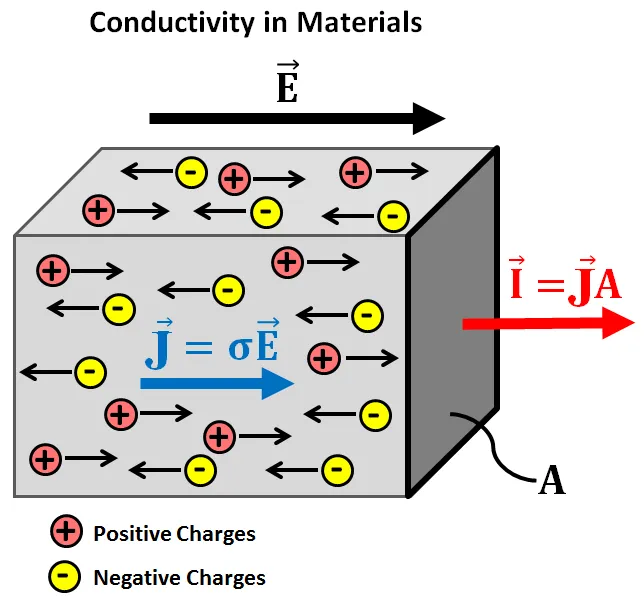
The current density J inside of a conductor depends on the electric field E and the material properties. Generally this dependence is very complex, but in special cases like metals the current density J is proportional to the electric field E. In that special case the ratio of the magnitudes of E and J is constant. By supposing that this is true for every case we start defining new things.
The electrical resistivity (or special resistance) of a material is noted as ρ and equal to the ratio of the electric field E by the current density J.
That way the equation for electrical resistivity ρ is:

The higher the resistivity, the stronger is the electric field required and the smaller the electric current density produced by the electric field.
Electrical resistivity ρ is calculated in:
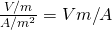
where 1 V/A is noted as 1 Ω (ohm) and so ρ is calculated in:
Ω*m (ohm-meter)
something that we will cover more next time!
An ideal conductor would have a resistivity "zero", whilst a ideal insulator would have "infinite" resistivity, but of course there is nothing "perfect" like that in nature!
Metals and Alloys have the smallest value of electrical resistivity and so are great conductors. The special resistance of insulators is much much higher then the resistivity of metals and alloys by a enormous factor of 10^20+!
Here's a table of electrical resistivities:
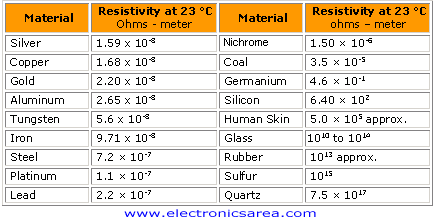
You can see that the metals and alloys have very small resistivities in the order of 10^-8 up to 10^-6, whilst insulators have 10^10 up to 10^17 resistivity!
Worth noting is that Silicon, which is an popular semiconductor, has a resistivity of around 10^2 that puts it into a sweet spot in the center of the "scale". This shows us why semiconductors act like both depending on the situation!
Also note that:
Good conductors of electricity are mostly also great conductors of heat! On the other hand insulators of electricity are mostly also bad conductors of heat. This is true, because heat is also related with the electrons motion!
Semiconductors are special not only because of the electrical resistivity, but because they are also affected by changes in temperature (heat) and also by small quantities of mixtures!
Electrical conductivity
The ratio of J and E at constant temperature was discovered by G.S. Ohm and that's why the equation that we saw previously is called Ohm's law.
A material that obeys Ohm's law sufficiently is called an ohmic conductor. On the other hand, materials that have a high deviation/difference to Ohm's law are non-ohmic conductors.
Of course this law again applies to ideal materials!
Some info from wikipedia.
The opposite ratio J/E is called electrical conductivity and shows us how conductive a material is! Good conductors of electricity of course have a high value of electrical conductivity, whilst insulators will have smaller values. (similarly we can also define thermal conductivity)
Thermal coefficient of electrical resistivity
The electrical resistivity of a metal conductor mostly increases when we increase the temperature. This of course means that the electrical conductivity of a conductor decreases when increasing the temperature. This can all be understand better if you think of the motion of the electrons. With higher temperature the motion is even more randomly, making it more difficult to orient them to follow one specific direction.
For a small range of temperatures (approximately 0 up to 100 °C) the electrical resistivity of a metal can be calculated approximately using the equation:
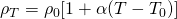
where:
- ρ0 is the electrical resistivity for some reference temperature T0
- ρT is the electrical resistivity at a temperature T
- α is the so called Thermal coefficient of electrical resistivity
Here a table with some of those coeffients:
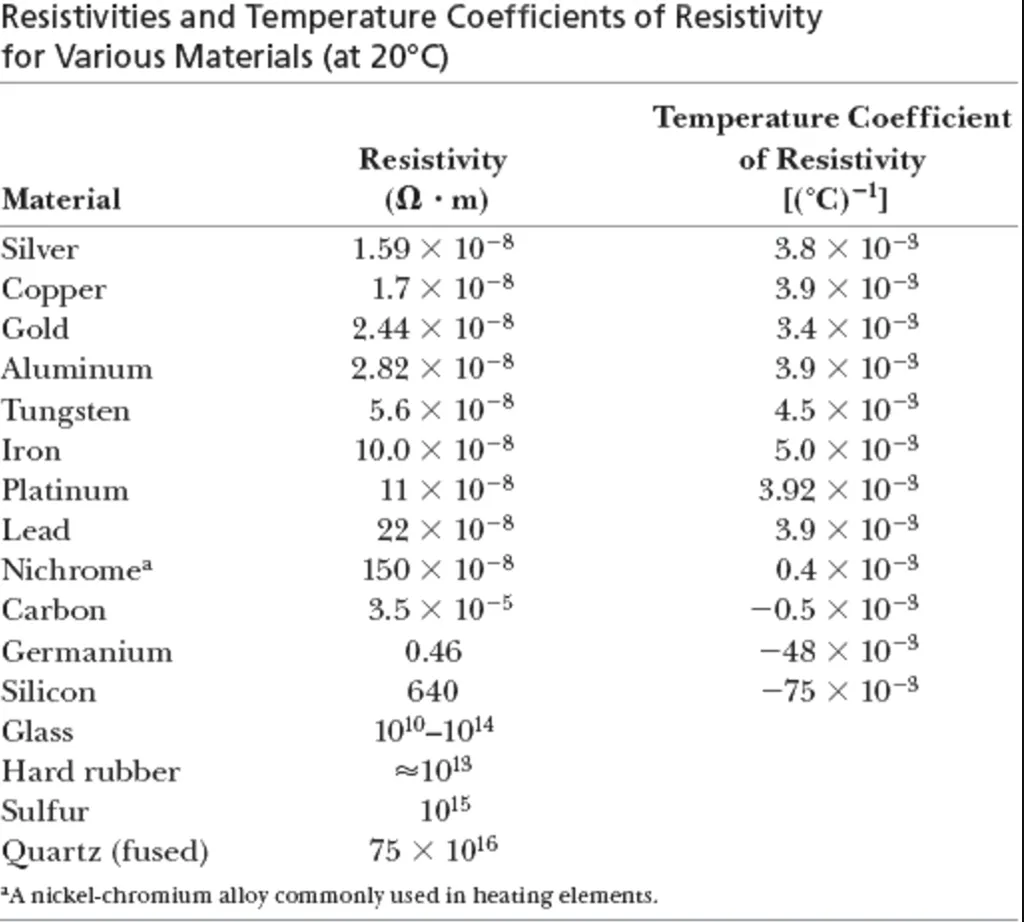
It's worth noting that Carbon has a negative coefficient which means that the special resistance is decreasing when the temperature increases!
The resistance of a semiconductors decreases drastically when the temperature increases. That's why a specific small crystal semiconductor called thermistor is used as a sensor of temperature! Other materials like carbon and platinum are also used in thermometers!
Hyperconductivity
Something interesting is a phenomenon called hyperconductivity which happens for some metal alloys and acids. While the temperature is decreasing, the special resistance is at first also decreasing smoothly, something which is similar to every other metal. But, after a critical temperature Tc we observe a phase transition and the electrical resistance nullifies (changes to zero) sharply! Something which of course means that the electric current flowing through such a material keeps on going, without the need of an electric field E!
But, don't be happy! This phenomenon was observed at temperatures of 4.2K, 20K, 77K and the most recent value 125K (Kelvin) which of course is -148.15 °C! So, getting into room temperature is not far away :P
The discovery of some mixture which gets hyperconductive in a more reasonable temperature would bring a number of positive consequences which would of course help with the energy distribution around the globe!
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
Electric current -> Electric current, current density
And this is actually it for today!
Next time I will cover Electric Resistance (easy to confuse with today's topic!).
Bye!
