Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to get into Electric current!
All the mathematical equations will be drawn using quicklatex!
So, without further do, let's get straight into it!
What is Electric current?
In Electrostatic situations, that we talked about until now, there where no moving charges which means that the electric field inside of the conductor is zero.
So, what happens when the charge is moving?
This is exactly what we will discuss today...
Electric current is described as:
Any movement (or flow) of charge from one area to another.
To keep this electric flow going, a constant force needs to be applied to the charges inside of a conductor so that they keep moving. So, let's suppose that there is an electric field E inside of the conductor so that an electric force F = qE acts on each charge q.
As already told in previous posts, what moves are electrons which of course are very easy to move in high speeds. When an electron is inside of a vacuum then it of course accelerates constantly, but when moving inside of a conductive material, like a metal, then the motion of electrons is different, because of the collision of the electrons with the particles of this material. The motion of the "free" electrons inside of a metal is random, like air molecules, but they of course move in much higher speeds!
The electric field E that is applied inside of a metal (which is a conductor of electricity) of course applies a force to those free electrons which makes them move slowly (or slip/drift, because of friction) to the direction that this force gets applied to. This force acts on the random motion of those electrons making them follow a specific direction/path. The electric field produces a work on those moving electrons and the resulting kinetic energy is transferred to the metal causing the ions to oscillate, something which of course produces heat!
That way the motion of the electrons is build up of two motions:
- a random motion with high velocity
- a motion "controlled" by the force of the electric field with a smaller velocity
Definition of Electric current
Electric current is the quantity of charge that moves by time. In metals we always have (negatively charged) electrons moving around, but in ion solutions sometimes both electrons and protons are moving!
The following picture shows us a diagonal cut of a conductor, where positive q charges are moving to the right:

Supposing that the electric field also goes in that direction, the electric current I that passes through the surface A by unit of time is of course given by:
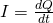
where:
- dQ is the charge that moves through the area A in
- dt amount of time
Note that the current caused by electrons (negative charges) moving in the opposite direction is equal to the current of positive charges.
Electric current is a scalar unit (not vector!) and calculated in Ampere (A), where:
1A = 1 C/s (coulomb/second)
Of course current will be calculated in mA, μΑ, pA etc. and so we will always have to convert into A to do calculations!
Current density
Another way of defining current is using the slip (or drift) velocity of the moving charges, which is how fast they move in the direction that the electric field causes them to move.
Suppose we have the same picture as before and so an electric field with direction left-to-right and an intersection/cut of A area. Also, the charges that move through it are again positive. The force that acts on those charges is applied in the left-right direction and by also considering the field being uniform we then have the same properties for each point and so all the directions are equivalent.
Let's say that we have a definite number n of charges per volume unit, which is also called charge carrier density (in m^-3). Let's also consider them all having the same "drifting" velocity with magnitude v. The charges that leave the right base of the surface A at dt time (with length v*dt) are the same ones that where inside of the surface at the beginning of dt time. The volume of the cylinder is n*A*v*dt.
Cause every charge has charge q the total charge dQ is:

By putting this into the first equation of current we get:

which is another equation for electric current.
The current per area is called current density J and equal to:

which is a vector unit calculated in amperes per square metre!
By having negative charges the electric current stays the same (as I already told before), cause the negative charges moving to the left (force gets applied right-to-left) increase the positive charge in the right side of the intersection!
Different charges moving
One last thing remains to discuss..
I told you that in some cases both positive and negative charges are moving inside of the conductors (like for example in ion solutions or semiconductors).
How do we calculate the electric current and current density in such cases?
In the general case where an conductor contains the charges q1, q2, ... with density n1, n2, ... and drift velocities v1, v2 etc. the electric current I is calculated using:

By diving with A we get the current density J which is:

The direction of the drift velocity v is the same with the electric field E when having an opposite charge and in the opposite direction when having a negative charge, but either way the product qv has the same direction with E.
The vector unit of current density J always has the same direction with the electric field E!
From now on we will always consider the current being caused by positive charges even if the actual conventional current direction is in the "opposite" direction most of the times.
Of course in a closed circuit the electric current is the same for all the points of the circuit, which means that the number of charges that is entering a intersection/cut (and so electric current) is the same for all the intersections. This is all true because of the conservation of charge!
One last thing that you should always remember is:
Electric current originates from a positive (source) pole and is consumed until it reaches a negative (termination) pole.
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
Applications of Gauss's law (part 2) -> more Gauss applications
Electric flux exercises -> examples in electric flux and Gauss's law
Electric potential energy -> explanation of work-energy, electric potential energy
Calculating electric potentials -> more stuff about potential energy, potential, calculating potentials
Equipotential surfaces and potential gradient -> Equipotential surface, potential gradient
Millikan's Oil Drop Experiment -> Millikan's experiment, electronvolt
Cathode ray tubes explained using electric potential -> cathode ray tube explanation
Electric potential exercises (part 1) -> applications of potential
Electric potential exercises (part 2) -> applications of potential gradient, advanced examples
Capacitors (Condensers) and Capacitance -> Capacitors, capacitance, calculating capacitance
How to solve problems around Capacitors -> combination, solving problems, simple example
Electric field energy and density -> Electric field energy, energy density
Dielectric materials -> Dielectrics, dielectric constant, permittivity and strength, how to solve problems
Electric capacitance exercises -> examples in capacitance, energy density and dielectrics
And this is actually it for today!
Next time I will cover Electrical resistivity (or special resistance)!
Bye!
