
Introduction
Hello it's a me again Drifter Programming!
After the quick introduction to this new Physics branch called Electromagnetism we continue on talking about a law that describes those electric interactions.
Today's post is all about Coulomb's law and some examples/applications of it.
So, without further do, let's get straight into it!
Coulomb's law
Coulomb was an scientist that studied the forces and interactions between charged objects.
Doing a lot of experiments he found the mathematical equation of the Electrostatic Force between two point charges q1 and q2 that have a distance r.
The force F is equal to:

where k is the Coulomb constant that depends on the metrics that we are using.
Coulomb's law is described like that:
The magnitude of the electrostatic force of attraction or repulsion between two point charges is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them
from wikipedia
Because of Newton's 3rd law we know that each force (action) has an equal, opposite reaction.
This means that those forces will be on the same "line" and that the 2 forces will be opposite and equal in meter even when the charges are not equal.
The actual electric charge is calculated in Coulomb's (C) in SI.
You can read about it here in wikipedia.
Superposition principle
Coulomb's law covers the interaction between two point charges, but what about 3, 4 or more?
Well, the same way as we "added" forces in Classical Mechanics when having Friction, Gravity etc. to get the component vector for each axis, we again can do the same for electrostatic forces!

This will also be used in more advanced "Object-Physics" that we will get to later on...
When two point charges apply a force to a third point, the total force asked to it will be the vector addition of those forces, like if they applied each force on their own.
This important property is a cause of the superposition principle, and it can be applied for any number of charges!
Coulomb constant
Depending on the "environment" we have to use an specific Coulomb constant each time.
When in a vacuum this constant is approximately equal to:

This is the value that we will mostly use...
The Coulomb constant is given by the equation:
where ε0 is the electric constant of "vacuum permittivity".
Later on in Optical Physics (and other branches) we will also use a constant that depends on the speed of light...
Anyway the actual equation of Coulomb's law now after all this is:

where ε = ε0*εr and so equal to the product of "vacuum permittivity" times "material permittivity".
How to solve problems around Coulomb's law
Always keep in mind the following things:
- Use the correct SI metrics! Using k = 1/4πε0, we have to use meters for the distance r, coulomb's for the charge and force in newton's.
- When having more charges remember the superposition principle and use the vector addition of the forces applied to each charge! This also means that you have to distinguish the scalar and vector units.
- When the forces are in different axes, don't forget to use component vectors! Sometimes we may also need integration...
Examples
Let's now get into some examples that use this Law!
1.
Suppose two point charges that are on top of the positive x-axis.
q1 = 2nC and is r1 = 2cm away of the center of the axes (0, 0)
q2 = -3nC and is r2 = 4cm away of the center of the axes (0, 0)
Calculate the total force applied of those two charges (q1 and q2) to a third charge q3 = 5nC at the center of the axes.
Solution:
Because of the superposition principle we know that the total force will be equal to the vector addition of those two forces.
First we have to convert the nano-Coulomb's (nC) to Coulomb's (C)and the centi-meters (cm) to meters (m):

Let's now calculate each force alone and then do the vector addition:

F1 is of course in the negative direction because q3 and q1 have the same sign and repel, whilst F2 is in the positive direction because q3 and q2 have an opposite sign and so are attracted.
That way:

There are no components in the y and z axes and so the total force will repel q3 to the left.
2.
Suppose two point charges with charge q = 2μC and that they interact with an third charge with charge Q = 4μC.
Find the meter and direction of the total force applied to Q using the diagram:
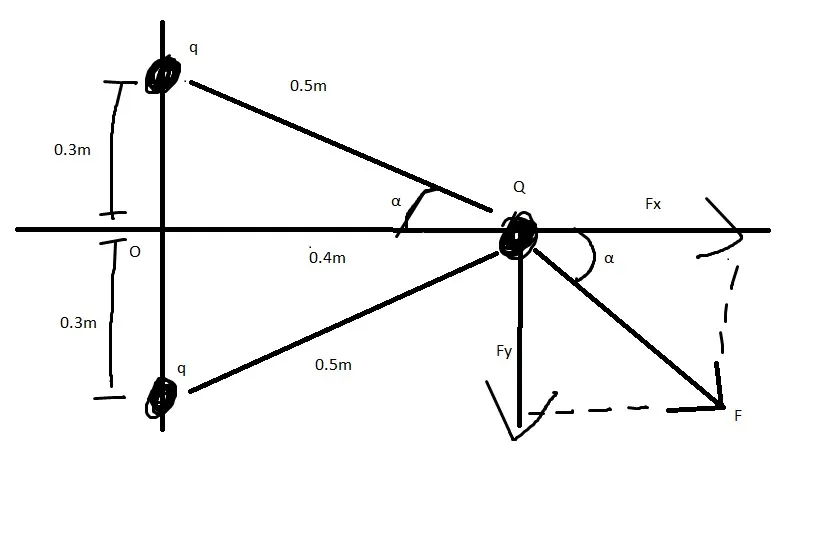
which shows the force applied of the upper charge...
Solution:
You can clearly see that we now have an angle and so will have component vectors for each axis (x and y). But, because the distances and charges are equal we can use the same equation to calculate the force applied from any of the two objects in value.
The metrics are right except the charge which has to be converted to Coulomb's.
So, because of Coulomb's law the force applied is:

Which means that each charge q applies a force of 0.29N to Q.
Let's analyze this force to component vectors...

Of course the charge on the bottom applies a force with the same meter, but opposite direction in the y-axis and so they cancel each other out which means that the total force on each axis is:
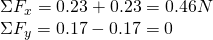
And so the total force applied to Q is going to the +x direction and has a meter 0.46N.
IMPORTANT NOTE:
When there is a force on more then one axis then we also have to give the angle (or tangent) between each component.
So, if there still was a force on the y-axis we would also say:
tanθ = Fy/Fx => θ = ...
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
And this is actually it for today's topic and I hope that you enjoyed it!
Next time we will get into Electric fields and forces!
Bye!
