
Introduction
Hello it's a me again Drifter Programming!
Today we continue with Electromagnetism to talk about some more Applications of Gauss's law! I highly suggest you to read the previous post, cause there I explain how we apply Gauss's law, have some critical points/tips and also some of the applications!
So, without further do, let's get straight into it!
Gauss Applications
Let's get into some more Applications of Gauss...
Electric field of an infinite sheet of charge
Let's calculate the electric field that is generated by a large (and actually infinite) uniformly charged sheet with area density σ.
We will use a cylinder Gaussian surface with the axis vertically across to the sheet charge and let's say an area A. There of course is a symmetry, cause we can "slide" the cylinder to any parallel direction without changing the meter of the electric field E.
This looks like this:

The electric field of E is of course vertically across to the sheet and parallel to the side of the cylinder. That way the electric field's meter is zero in the side of the cylinder and equal to EA for each base (2EA in total).
The total charge of the sheet is q = σ*A.
So, the Gaussian Integral gives us:

We can get the same conclusion by using Coulomb's law, which leads to more complicated math that I even left out for the exercises post that we had in that "part" of the series!
This clearly shows us that Gauss's law just works better for this case!
But, don't forget that we supposed an uniform electric field (and so uniformly distributed electric field lines) and that the meter of the electric field doesn't depend on the distance. Also, the sheet is considered of "zero" thickness, which of course is idealized cause nothing in nature has actually zero thickness! Either way this is a very good approach which works for points that are very close to the surface, where the field is considered almost uniform and vertically across to the sheet.
Electric field between parallel conductive plates with equal and opposing charges
Let's now suppose two large parallel conductive plates with equal and opposing charge. The area density of the charge is +σ for the one and -σ for the other charge plate. What kind of field is created in the space between those plates?
Because the two charges are attracted more charges are gathered in the surfaces inside.
Only a little amount of charge is distributed in the other side and when the length is supposed infinite then this charge can be ignored.
By also supposing that the field generated is uniform and that the charges are distributed evenly in the opposing surfaces we of course end up with the following field:
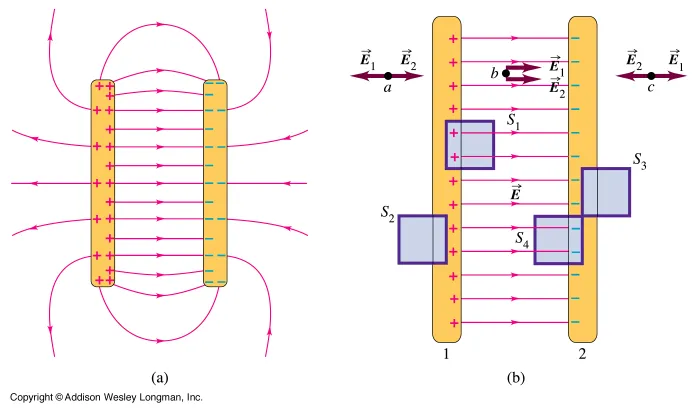
Using the previous application we can now say that the electric field of each of those plates is of course equal to the electric field generated by sheet's of charge, because the charges are gathered in one side "like" being a sheet.
The electric field outside of those plates is of course zero, cause the two electric field's cancel each other out!
Because the field lines go + -> - the electric field is equal to the vector sum of the two fields E1 and E2 (that in the inside have the same direction), which of course is:

Of course this prove was based on the previous application, but you could also use "square" surfaces instead!
Uniformly charged sphere
What is the electric field inside of an uniformly charged (across the whole volume) sphere of radius R in distance r < R?
The total charge of the sphere is Q.
This is the "other part" of the application that we had in the previous post...
We choose a Gaussian surface which is a sphere of radius r that is concentric to the charged sphere.
The volume density of the charged sphere is:

Supposing that the volume that is enclosed by the Gaussian sphere is 4/3 πr^3 we have the following total enclosed charge:

Because the area is symmetrical we know that the electric field is equal at points with the same distance and that the direction of the electric field is radially going outwards.
The total area of the Gaussian surface is 4πr^2 and so the integral gives us 4πr^2E.
By using the enclosed charge of before we now end up with:

In the center of the sphere (r = 0) the electric field is of course zero!
Something interesting is that for r = R we get the equation of the "other" application and so the meter of the electric field exactly at the "borders" which is:

This shows us that the electric field on top of the surface is the same as if we had the charge gathered in the center of the sphere, which as we have seen in the "other" application is true for any distance r > R!
The following is a diagram that shows us the electric field E and how it depends on the distance r:

- For r<R the electric field E is proportional to r
- For r>R we have E being proportional to 1/r^2
Next time we will get into some actual mathematical examples...
Previous posts about Physics
Intro
Physics Introduction -> what is physics?, Models, Measuring
Vector Math and Operations -> Vector mathematics and operations (actually mathematical analysis, but I don't got into that before-hand :P)
Classical Mechanics
Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
Rectlinear motion exercises -> examples and tasks in rectlinear motion
Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
Projectile motion as a plane motion -> missile/bullet motion as a plane motion
Smooth Circular motion -> smooth circular motion theory
Plane motion exercises -> examples and tasks in plane motions
Force and Newton's first law -> force, 1st law
Mass and Newton's second law -> mass, 2nd law
Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
Contact forces and friction -> contact force, friction
Dynamics of Circular motion -> circular motion dynamics, applications
Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
Contact force and friction examples -> exercises in force and friction
Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
Advanced Newton law examples -> advanced (more difficult) exercises
Electromagnetism
Getting into Electromagnetism -> electromagnetim, electric charge, conductors, insulators, quantization
Coulomb's law with examples -> Coulomb's law, superposition principle, Coulomb constant, how to solve problems, examples
Electric fields and field lines -> Electric fields, Solving problems around Electric fields and field lines
Electric dipoles -> Electric dipole, torque, potential and field
Electric charge and field Exercises -> examples in electric charges and fields
Electric flux and Gauss's law -> Electric flux, Gauss's law
Applications of Gauss's law (part 1) -> applying Gauss's law, Gauss applications
And this is actually it for today and I hope that you enjoyed it!
Next time we will get into Electric flux exercises!
Bye!
