[Image 1]
Introduction
Hey it's a me again @drifter1! Today we continue with Physics and more specifically the branch "Classical Mechanics" to get into Work and Power in Angular Moton. So, without further ado, let's get straight into it!
Work in Angular Motion
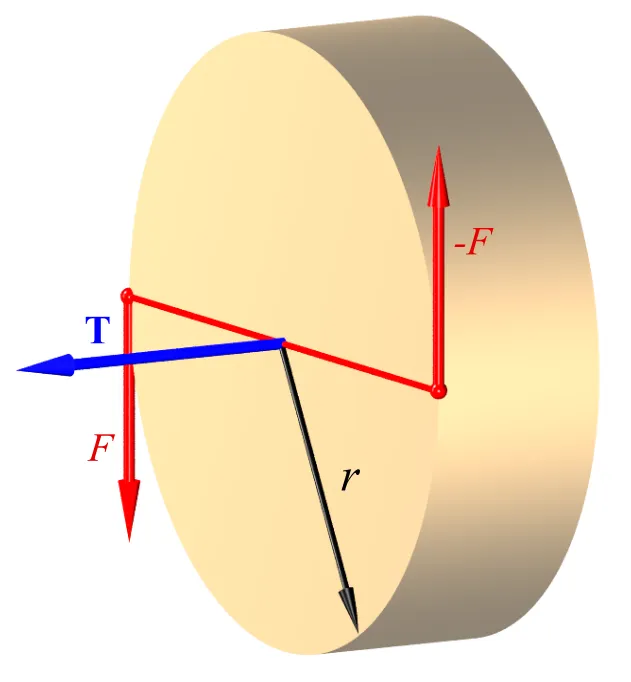
In angular motion we define the change in position as the change of the angle θ. With that in mind think about a rigid body that rotates through an angle dθ from some point A to point B, while a force F is applied to a point P. As we described in a previous article, the position of this point is defined by the vector r. To make the calculation procedure simpler, let's suppose that the rigid body is constrained to rotate about a fixed axis O. That way vector r moves in a circle of radius r. The arc length s of the circle if equal to s = θ·r. Because vector r moves in a circle, and by also defining the change in angle as a vector θ we can end up with the following cross product that will give us the change in arc length as a vector: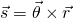
From the small change in angle dθ and because dr = 0, from the assumption of having the rigid body fixed on O, we get:

From the definition of Work in integral form we obtain:

So, the total work done on a rigid body is equal to the sum of torques integrated over the angle which the body rotates. A more descriptive way of writing the formula is:

where someone can clearly see the change from some angle A to B
If the complete body rotates through the same angle the so called incremental work is equal to the sum of torque times the common incremental angle dθ:

Work-Energy Theorem
Similarly to Translational motion, the Work-Energy Theorem also works for Angular motion. Thinking about a rigid body rotating around a fixed axis we have:
For Rolling motion (translational + angular) the Kinetic Energy for A and B will be equal to the sum of each kinetic energy, as we described in the previous article:

Power in Angular Motion
As you might remember, Power is equal to rate of doing Work. So, it's the change of work over time. Thinking about a constant net torque and the simple equation of Work that we defined previously (W = τθ), the power of angular motion is given by the equation:
Examples around all the equations that we covered today and in the most articles, will be done in a separate article, when we are finished with angular motion!
RESOURCES:
References
- https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_I_-_Mechanics%2C_Sound%2C_Oscillations%2C_and_Waves_(OpenStax)/10%3A_Fixed-Axis_Rotation__Introduction/10.8%3A_Work_and_Power_for_Rotational_Motion
- https://opentextbc.ca/physicstestbook2/chapter/rotational-kinetic-energy-work-and-energy-revisited/
- http://farside.ph.utexas.edu/teaching/301/lectures/node105.html
Images
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
- Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
- Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
- Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
- Internal Energy and Work -> Internal Energy, Internal Work
Momentum and Impulse
- Conservation of Momentum -> Momentum, Conservation of Momentum
- Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
- Collision Examples -> Various Elastic and Inelastic Collision Examples
- Impulse -> Impulse with Example
- Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
- Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis
Angular Motion
- Angular motion basics -> Angular position, velocity and acceleration
- Rotation with constant angular acceleration -> Constant angular acceleration, Example
- Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
- Parallel Axis Theorem -> Parallel axis theorem with example
- Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
- Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
Final words | Next up
This is actually it for today's post! Next time we will get into Angular Momentum...and the "famous" Conservation of Angular Momentum!
See ya!


Keep on drifting!

