Physics - Classical Mechanics - Work and Kinetic Energy

0
a few seconds ago
in#physics

[Image 1]

Introduction

    Hey it's a me again @drifter1! Today we get back to the Physics branch "Classical Mechanics", which is a series that got interrupted by lots of other series, to start talking about Work and Kinetic Energy. From this article and on, articles from the Physics, Mathematics and other similar "Educational" series will cover many different topics at once, so that they become much larger, more complete and more interesting articles. Covering only one topic (or 2-3) per article made lots of articles very boring even for me. This means that whole "chapters" might now be covered in one single "big" article. For example today's article will even include Exercises by the end, but also in-between to explain things better!

More specifically, today's topics are:

  • The definition of Work
  • Work by a constant Force
  • Work by a variable Force
  • Work and Kinetic Energy
  • Power
  • Exercises around everything

So, without further ado, let's get started!

What exactly is Work (In Physics)?

    Until now in this series we covered the motion of objects in one (rectlinear motion) and 2 dimensions (plane motion). This motion could be influenced by Forces that are applied on them. Analyzing such problems was easy using Newton's laws. What we don't covered is how much energy is being "lost" when applying an external force on an object's motion. That's when Work comes into play.

    In Physics, Work is the measure of how much energy is being transferred to an object when this object is moved over a distance by an external force which is applied in the direction of the displacement. [1]

    I have to note here that: Work is not accomblished only by the force acting along the displacement path of a body as a whole from one place to another, but can also occur when compressing gas, rotating a shaft and even when causing particles to move inside with external magnetic force.

    In this branch of mechanics we will mostly say that a force does no Work, unless the object is being displaced in some way having a component force along the path of displacement over which the object is moved. So, Work will be somehow defined as the force causing the movement of an object. For example, the force that we apply to pull an object and drag it around, by overcoming the friction forces, of course does Work. A book falling from a table and hitting the ground also has to do with the Work of another force, which is Gravity, and always acts in the downward direction. So, what is not Work? Well, easy! Let's consider that you are pushing a wall that doesn't move when applying this Force. You don't overcome the Inertia effect of the wall and your total Force is being cancelled out by the re-action of the wall, which is a force with the same magnitude but opposite direction (Newton's 3rd law of motion). In this case you surely "consume" energy and get tired, but don't transfer energy to the heavy stationary object, which is the wall, meaning that you don't actually do Work in terms of Physics! So, from all this we understand that holding something stationary even on top of our hand is not Work, as the same could also happen when placing this weight on a table. In such cases we just oppose the effects of gravity and act as the re-action force that has the same magnitude as the gravity/weight force but opposite direction and which we commonly note as N.

     Work as a magnitude is equal to the force along the displacement path multiplied by the displacement of the object (in vector terms). So, a simple mathematical equation for Work is:

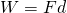
where:

  • W stands for Work
  • F is the Force
  • d is the displacement

From this equation we can already see that the SI unit of Work is:

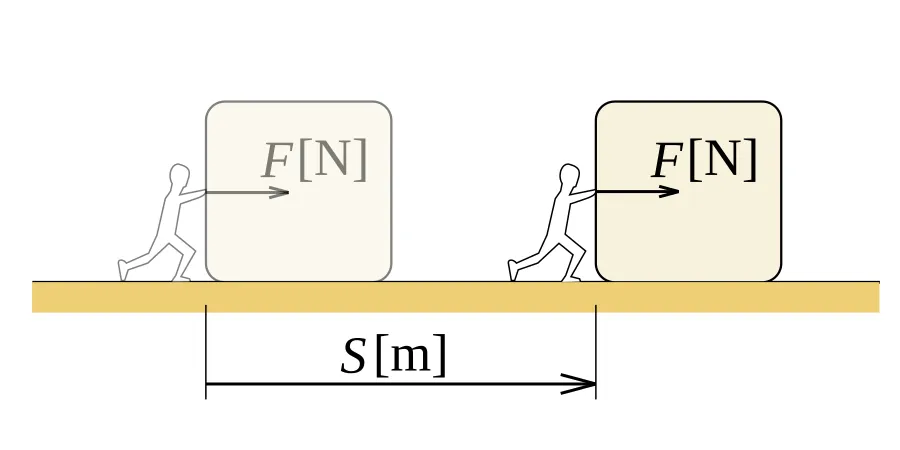
     So, Work is calculated in Joules, which are equal to the Newton's times the meters. This is also the unit of energy, as Energy is the ability of something to do work. This Energy can be stored and measured in many forms: kinetic energy, thermal energy, etc. Sometimes we tend to calculate Energy in Calories, which you all are familiar with from food. One Calorie is defined as the amount of energy which is required to raise 1 kg of water by 1° Celsius, which is equal to 4184 joules. This means that one typical 60 gram chocolate bar that contains 280 Calories of energy stores 1.17 million joules or 1.17MJ of energy! Considering a heavy box that we have to push with at least 500N, we would need a displacement of:

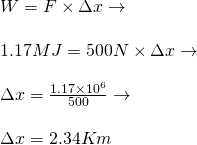
      We know that are bodies are 25% efficient at transferring stored energy from food into work and so considering a pushing speed of approximately 0.25 m/s (normal walk speed) we would need to push for:

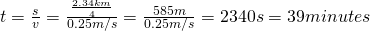
Yes that's a lot of time :P

Let's get into the mathematics and cases more in-depth now.

Work by a constant Force

    The simplest case is having a constant Force. In that case the work done by the constant force is proportional to the force applied times the displacement of the object. First of all you should learn to distingush displacement and distance travelled. Distance is not always the same as displacement, meaning that we can use the actual distance only when the force is being applied along the displacement path. When not then we have to calculate the actual displacement or the "part" of the total distance travelled at which the Force did Work on the object.

     Having a constant Force that is applied along the displacement path the Work is simply calculated as:

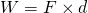
which is the equation that we mentioned earlier.

    Let's now consider that the Force is applied at an Angle to the displacement. This is also the usual case, as force rarely acts parallel to the direction of motion. Until now the motion was considered one-dimensional as you could also see in the chocolate example, where I used the displacement at the x-axis (Δx). When Force is applied on an angle we get into 2 or even 3-dimensions, depending on the actual motion of the object. Having the angle be zero along the total direction of motion, the force is again applied parallel to that motion, applying the most Work. This tells us that we have to use a cosine term, which is equal to '1' when the angle is zero (cos0° = 1). As we increase the force angle in respect to the direction of motion, less and less work is done along that direction. When reaching an angle of 90° (or π/2 rads) the force is being applied perpendicular to the original direction of motion, meaning that no Work is done in the direction of displacement, as the cosine term now gives us zero (cos 90° = 0). This means that we now do Work in another direction.

By also considering an angle θ we now end up with the equation:

    It's worth noting that we can also write the Work as an integral of the Force in respect to x,  where we can afterwards also consider the angle:

Let's push a Box [From Reference_4]

Let's consider that we are pushing a Box along the x-axis in a 2D-system (x and y axes).

We can come up with the following scenarios:

  1. box pushed parallel to the x-direction
  2. with an angle of 45 degrees to the x-direction
  3. with an angle of 60 degrees to the x-direction
  4. with an angle of 90 degrees to the x-direction

1.

    The first case is pretty straight forward. Applying force parallel to the direction of motion, Work is being done only along the x-direction, which is the direction of motion. This means that the Box doesn't move at the y-direction, since all the Force is acting parallel to the x-direction with an angle of zero. In that case the total work is just F times displacement in x-axis.

2.

    When pushing with an angle of 45 degrees in respect to the x-direction, we also have an angle of 45 degrees to the y-direction. The cosine of 45 degrees gives us 1 / √2, which is approximately 0.71. This shows us that 71% of the total force is contributing along the x-direction, whist the remaining 29% is acting along the y-direction. In this case the object will also start moving along the y-direction.

3.

    Similarly, we now have an angle of 60 degrees in the x-direction and also an angle of 30 degrees in y-direction. The cosine of 60 degrees gives us 1 / 2 meaning that an equal amount of force (50-50) is acting in the x and y-direction. So, the work is no done linear with respect to both x and y.

4.

    Lastly, when applying Force perpendicular to the x-direction, no work is done in that direction. In other words, the box is now being pushed only in the y-direction, meaning that the total work (100%) is being done in the y-direction. That way the work done in the x-direction is zero.

Work by a variable Force

    Until now we saw that force can be applied parallel to the object's motion and also with an angle in respect to that motion. But, in all these cases the actual Force magnitude always remained constant. When applying variable Force we have to use Integration. So, the Work done by such a Force will be equal to the Integral of Force in respect to time as:

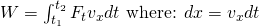
     This means that the Force will now be given as a function of time! Also note that the velocity/displacement is considered being along the x-axis. Nothing really special really, you just need to be good in Mathematical Analysis to solve this kind of Integrals :D

    Sometimes we also use integration to calculate the work done by constant Forces (as mentioned earlier already), cause the integration of the product of force and distance is the general way of determining the work done by a force on a moving body.

    For example in Thermodynamics the Work of Pressure (Force / Area), considering that the pressure P is constant (can be taken out of the integral) is given by:

    Another great example is gravity! Gravity is a constant force that is applied on free-falling objects along the y-axis (vertical motion). That way we can write:

     You can see that this is the same result that we would get by simply using the product of force and distance, as gravity is applied parallel to the motion of displacement and the displacement in that case is equal to the distance.

Work and Kinetic Energy

    We should first understand what Kinetic Energy is. Kinetic energy is the energy that an object has because of it's motion. When we want to set an object in motion, change it's direction, accelerate it, we must always apply a force. Applying this Force requires Work. This energy that is being transferred to the object that might leave the object with a new constant speed after the work is done, is turning into Kinetic energy. This energy is sure dependent of the mass and "final" speed/velocity achieved, but how do we get into an final equation?

Let's start with what we mentioned today about Work:

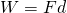
Let's substitute the Force with what we know from Newton's 2nd law:

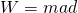
    Now things get interesting! You might be lost now, but don't worry I got ya :P You might remember from the kinematic equations of motion that we can substitute the acceleration if we know the initial and final velocity, as well as the distance travelled. I'm talking about the equation:

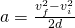
Substituting a in the previous one we get the following result:

 

     From this we can understand, that the net amount of  work done on an object changes the quantity 1/2 mv^2, which is the kinetic energy, mostly noted as K.

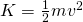
     In general, we say that the change in kinetic energy is equal to the net work done on an object or system:

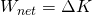
    This last equation is known as the principle of work and kinetic energy or the work-energy theorem. As you can see that theorem could be derived very easily from Newton's second law in addition with an equation that substitutes a for us (vf^2 = vi^2 + 2ad).

Therefore we can now calculate the Work done by a Force using:

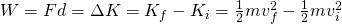
    So, when the final velocity is less then the initial velocity the Work of course comes out negative, meaning that we applied force in the negative direction, eventually slowing down the object. Sometimes we might even have a positive Work doing that, as the actual velocity is being squared, meaning that we can decrease the velocity and then increase it in another direction (opposite) by even passing the initial velocity magnitude!

Power

     Another interseting topic is the so called rate of doing work or amount of energy consumed per unit of time that we call Power. In general, Power is the measure of the rate of doing work or transferring energy and calculated in J/s, known as Watt (in honor of James Watt). For example the rate at which a lighbulb transforms electrical energy into heat and light is also measured in watts (noted as W). The more the wattage, the more the power and the more the electrical energy used up per unit time. As energy transfer can also be used to do work, power is also equal to the rate at which this work is performed.

From all this we understand that power follows the mathematical equations:

We will get back to more about Power after covering Potential energy!

Exercises around everything

    After covering all these topics let's now get into some nice examples and applications around them, so that you understand everything "in practice". Let's go!

Which Forces do Work? [Based on 2. from Ref_9]

    Let's start out with the most important topic, to check your understanding about what is Work and what is not. Consider the following 5 Cases of Free-Body Diagrams:

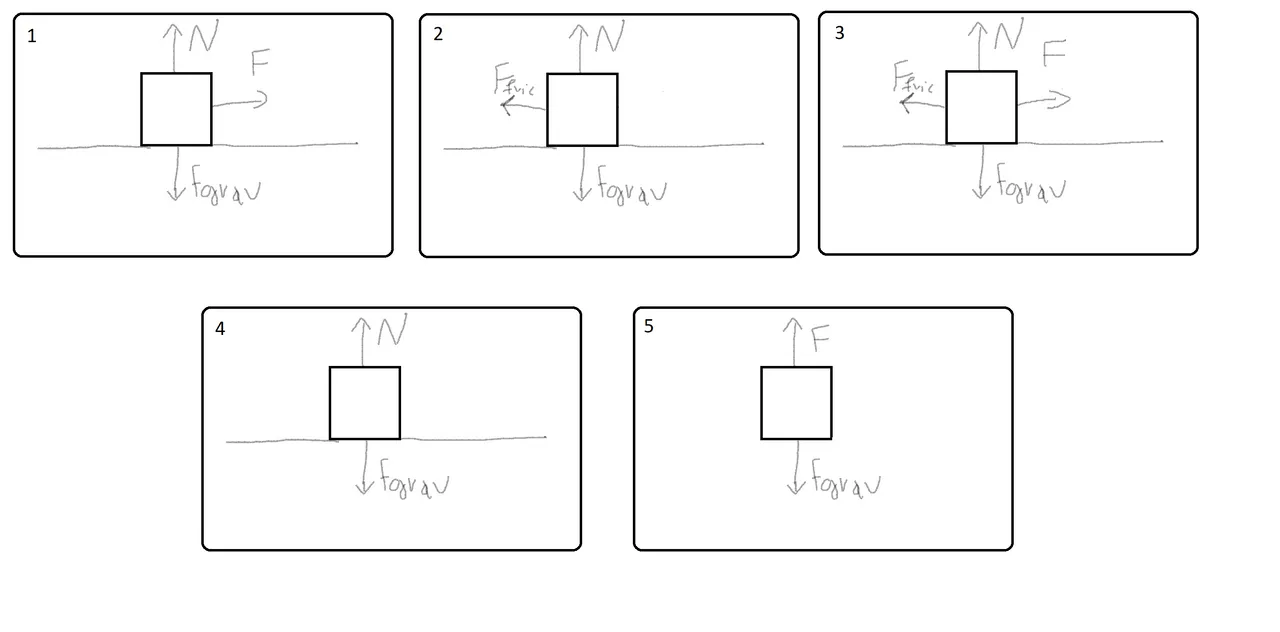
[Custom Digitizer drawing]

Explanation of each situtation:

  1. A force F is applied to push a block across a friction free surface
  2. A frictional Force slows down a moving block (that goes to the right)
  3. A force F is applied on the block to keep it moving at a constant speed across a frictional surface
  4. The object is sliding at constant speed across a friction free surface
  5. The object is being pulled upward at constant speed 

1.

    In this Case only the applied force F does Work as it is applied along the motion of the block. The other forces are applied perpendicular (or vertical) to the motion of the block, meaning that they don't cause any horizontal displacement (actually no displacement at all, as they are equal).

2.

    Here only the frictional force does work as it is the only force applied in the axis of the motion, even though it's in the opposite direciton doing "negative" work. The other's are again applied perpendicular to the motion doing no work.

3.

    In this case both the frictional force and the the applied force to work as they are both applied on the motion of the object. Because the object travels at constant velocity these works are equal and opposite, meaning that F does a positive work +W and the friction a negative work -W. The other two again don't do work along the axis of motion.

4.

    The two forces act perpendicular to the block's motion meaning that they don't do any work at the direction of motion. This means that the object just moves freely along the frictionless surface.

5.

    In this case both of the forces do equal, but opposite work as they are applied in the direction of displacement, letting the object move at a constant speed. Note that it's the only case of the 5 at which Gravity and our applied "vertical" force did work along the object's motion and work at all, as the block didn't move in the vertical axis at all in 1-4.

Work by a constant Force

Let's get into some examples around constant force work.

Example 1 (exercise 33. from Ref_10)

     A shopper pushes a grocery cart 20.0 m at constant speed on level ground, against a 35.0 N frictional force. He pushes in a direction 25.0º below the horizontal.

  1. What is the work done on the cart by friction?
  2. What is the work done on the cart by the gravitational force?
  3. What is the work done on the cart by the shopper?
  4. What is the total work done on the cart?

Solution:

1.

    The friction is applied in the opposite direction meaning that we expect a "negative" result. By using the "simple" constant force equation for Work we get:

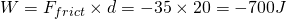
2.

    The gravity is applied perpendicular to the motion of the cart meaning that it doesn't do any work. Mathematically this can be expressed as:

3.

    The force done by the shopper can be calculated using the constant force equation with angle (that we will do first), but also directly from the problem as the cart is moving at constant speed, meaning that the magnitude of work of that force along the direction of motion is equal, but opposite in magnitude with the work done by friction. This and only this already tells us that the solution will be W = 700J.

Let's also use the mathematical equation:

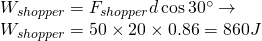
    We don't get the same result, as we don't used energy considerations, which actually give us a force of 38.6N by the shopper!

4.

The total net work done on the cart is equal to zero, as it doesn't change velocity:

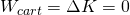
Example 2 ("Calculating Work" Example from Ref_11)

     A truck hitched to a trailer exerts a horizontal net force of 500.0 Newtons. If the trailer moves a total distance of 1525 meters, how much work was done by the truck? 

Solution:

We simply have to apply the work equation for constant force, which gives us:

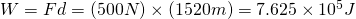
Practice (from the same Reference...)

Try to solve the following:

     A student exerts a vertical net force of 175 N on a stack of books. He does 350 J of work on the books. What vertical distance did he move the books? 

Solution is: 2m

You can also check out Example 7.1 at:

http://www.kshitij-iitjee.com/Work-done-by-constant-force/

which is similar to Example 1.

Work by a variable Force

Variable force can be calculated using integration...

Example from Ref_12

    Consider a force F = 2x +5 (N) that acts on an object displacing it from x = 0m to x = 2m. Calculate the Work done during that displacement.

Solution:

A simple integration:

...and also using a graph method that is explained the Example of:

https://www.desktopclass.com/notes/physics/work-done-by-a-variable-force-f-sc-physics-chapter-4-2.html

Work and Kinetic Energy

Let's get into examples around Kinetic energy and the Work-Energy Theorem...

Example 1 (exercise 35. from Ref_10)

     Compare the kinetic energy of a 20,000-kg truck moving at 110 km/h with that of an 80.0-kg astronaut in orbit moving at 27,500 km/h. 

Solution:

The kinetic energy of the truck is:

The kinetic energy of the astronaut in orbit is:

Therefore the ratio is:

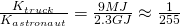
Example 2 ("Calculating Kinetic Energy" Example from Ref_11)

     A physics teacher exerts a force on a 6.36 kg bowling ball that causes the ball to move horizontally at 2.55 m/s. Calculate the kinetic energy of the bowling ball.

Solution:

We know everything and so can simply apply the equation of KE:

Example 3 (Based on the Example of Ref_13)

Find the speed of a package at the end of the push if:

  • the total net work is W = 92J
  • the initial kinetic energy is 3.75J
  • the mass of the package is 30Kg

Solution:

    Simple...we start with the work-energy theorem replacing what we know that calculate the final kinetic energy.

    By replacing the final kinetic energy with it's equation we can then find the velocity as following:

Power

Let's lastly also get into an application of Power...

Example (From Ref_14)

Find the power of a man who pushes a box 8m with a force of 15N in 6seconds.

Solution:

First of all we have to calculate the Work which is:

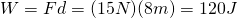
In this case it helps us to think about Power athe rate at which Work is performed meaning that:

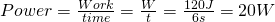
We haven't covered much more about it and so this was the best I could think about..

RESOURCES:

References

  1. https://www.britannica.com/science/work-physics
  2. https://www.thoughtco.com/work-2699023
  3. https://www.khanacademy.org/science/physics/work-and-energy/work-and-energy-tutorial/a/what-is-work
  4. https://courses.lumenlearning.com/boundless-physics/chapter/work-done-by-a-constant-force/
  5. https://courses.lumenlearning.com/boundless-physics/chapter/work-done-by-a-variable-force/
  6. https://www.khanacademy.org/science/physics/work-and-energy/work-and-energy-tutorial/a/what-is-kinetic-energy
  7. https://courses.lumenlearning.com/boundless-physics/chapter/work-energy-theorem/
  8. https://courses.lumenlearning.com/boundless-physics/chapter/power/
  9. https://www.physicsclassroom.com/class/energy/Lesson-1/Calculating-the-Amount-of-Work-Done-by-Forces
  10. https://phys.libretexts.org/Homework_Exercises/Exercises%3A_General_Physics/Exercises%3A_College_Physics_(OpenStax)/07%3A_Work%2C_Energy%2C_and_Energy_Resources_(Exercises)
  11. https://www.texasgateway.org/resource/work-energy-theorem
  12. http://tutor4physics.com/examplesvariableforce.htm
  13. https://opentextbc.ca/physicstestbook2/chapter/kinetic-energy-and-the-work-energy-theorem/
  14. http://www.physicstutorials.org/home/energy-work-power/power

Images

     All of the pictures that I used in this article are either mine or available under the Creative Commons (CC) License. 

Mathematical equations that I had in this post where drawn using quicklatex!

Previous articles of the series

Rectlinear motion

Plane motion

Newton's laws and Applications

      You can find all of my previous articles organized per category, per series, per chapter, per article, in my recap of Summer 2018!

Final words | Next up

    This is actually it for today's post! Next time we will get into Convervation of Energy by mainly covering Potential Energy. As this next topic has lots to things to cover, we will spit it into 2 or even 3 articles!

See ya!

Keep on drifting!

a few seconds ago
drifter10
$ 2.56
214
H2
H3
H4
3 columns
2 columns
1 column
2 Comments
Ecency