Hello it's a me again drifter1! Today we continue with Physics and more specifically Classical Mechanics by getting into the motion of projectiles. The whole post will cover everything that you have to know about this kind of motion, from equations, to examples etc.
Here you can find the previous post about the vectors in a plane motion, that you will need to understand the mathematics behind all these physics equations.
So, without further do, let's get straight into it!
A quick recap
In linear motion we talked about how an object moves on a specific axis and so dimension.
There can be 3 types of movements (that we all talked about):
- constant velocity and so zero acceleration that gave us the easiest equations (post)
- variable velocity, but with constant acceleration and so pretty simple equations (post)
- variable velocity and acceleration that needs mathematical analysis techniques like differentiation and integration (post)
In my previous post, where we started getting into plane motion or motion in 2 dimensions we saw that almost the same rules apply cause:
2-dimensional motion is build of two independent motions for each dimension/axis, where each can be of an different kind (constant/variable velocity, constant/variable acceleration) and therefore we can analyze each motion independently.
Projectile motion
A projectile, missile, bullet or any object that is shoot up in the air or to the air follows a projectile motion that is a special kind of 2-dimensional (plane) motion.
Such a motion is build up of:
- a free fall motion in the y axis where acceleration is constant and equal to gravity
- a constant velocity and so zero acceleration in the x axis if we suppose that the air resistance is zero
This means that we have to find the component vectors for the velocity vector u which are:
ux -> on the x-axis (u0x for the start velocity u0)
uy -> on the y-axis (u0y for the start velocity u0)
Now, each independent motion is being described by the following equations:
for the x-axis:
ux = u0x (constant),
x = x0 + u0x*t (linear motion with constant velocity)
for the y-axis (free fall equations):
uy = u0y - g*t
y = y0 + u0y*t - 1/2*g*t^2
So, now the question is:
How do we determine the component vectors and can we get even simpler equations that describe the same phenomena?
More specific Equations
Well, the same way as in my post about Vector Math, we need an angle a that is equal to the angle the velocity vector has to the x-axis.
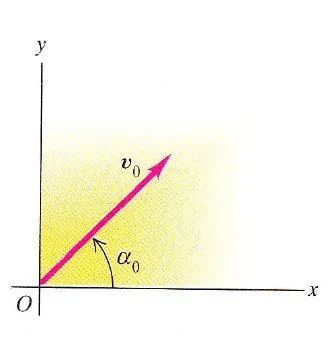
This angle changes as you can see in the picture where a0 is the angle of the velocity u0 we have at the beginning. If someone gives us the angle at any point of the curve that the object follows or we calculate it in some other way, we can then use the following to determine the component vectors and much faster equations that look like this:
u0x = u0 * cosa0
u0y = u0 * sina0
where we can also use the velocity vector at any other point, but we mostly know the starting velocity and angle only and so use the ones I gave you instead!
Replacing u0x and uoy in my equations of before we end up with:
x = x0 + u0*cosa0*t
y = y0 + u0*sina0*t - 1/2gt^2
ux = u0*c0sa0
uy = u0*sina0 - g*t
The displacement vector r looks like this:
r = xi + yj,
where x and y are the equations of above.
And has a meter of:
|r| = root(x^2 + y^2)
To find the meter of velocity at any point we use:
|u| = root (ux^2 + uy^2)
the same as in any other motion.
To find the angle we use the tangent of uy an ux:
tan a = uy/ux => a = arctan(uy/ux)
A projectile motion where we include all the vectors and angles looks like this:
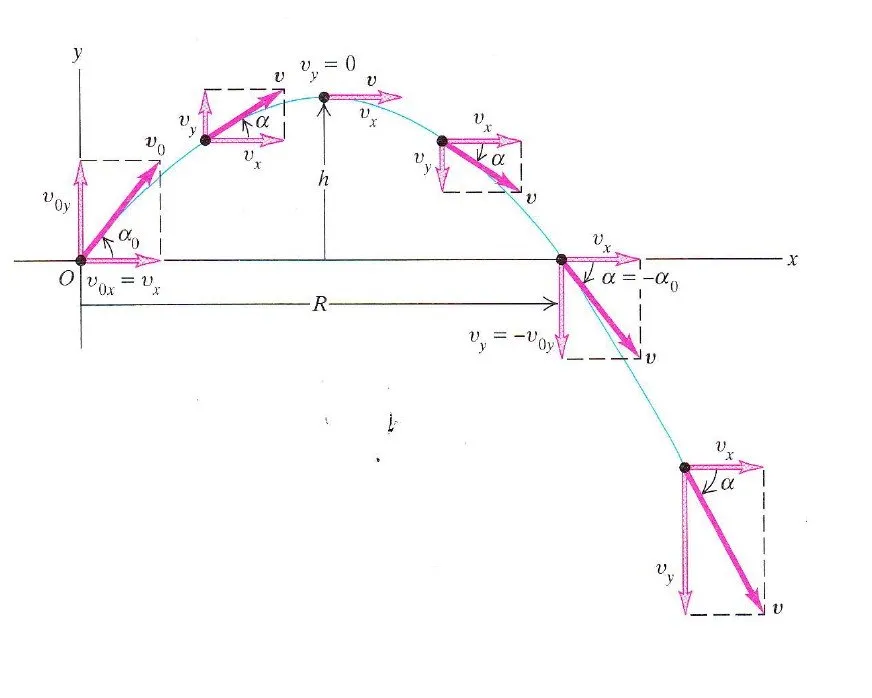
You can clearly see that we can find the value of velocity in any axis and in total, the acceleration, time, height (y-axis), distance traveled in the x-axis and even more by using the 4 simple equations!
A Parabola motion
We also have another mathematical conclusion that we get by seeing the curve and that can also be proven by mathematics.
The motion in the y-axis follows a parabola,
By removing time t from the equation of y using t = x/ (u0*cosa0) we get:

that is clearly a parabola y = bx - cx^2
Example motion
Question:
Suppose we know the following:
x0 = 0, y0 = 0 -> position
u0x = 5m/s, u0y = 0m/s -> velocity
ax = 0, ay = -g = -9.8 m/s^2 -> acceleration
Calculate the position and velocity at t = 1/4 seconds
Solution:
We already know the component vectors at the beginning and so we can directly use the equations we talked of earlier.
For the x-axis we have:
x = x0 + u0x*t = 0 + 5*1/4 = 1.2 m
For the y-axis we have:
y = y0 +u0y*t - 1/2gt^2 = 0 + 0 - 1/2*9.8*(1/4)^2 = -0.31m
The negative sign tells us that the object is 0.31 m down from where it was when it started.
We can also calculate the displacement in meters using the meter of r:
|r| = root(x^2 + y^2) = root(1.2^2 +(-0.31)^2) = 1.2m
Do find the velocity we use the equations again and so:
ux = u0x = 5 m/s, cause the motion in the x-axis has constant velocity
uy = u0x - g*t = 0 -9.8*1/4 = -2.4 m/s
The actual velocity meter is:
|u| = root(ux^2 + uy^2) = root(5^2 + (-2.4)^2) = 5.5 m/s
and the angle to the x-axis is:
a = arctan(uy/ux) = -26 degrees
And this is actually it and I hope that you enjoyed it!
For more information visit one of the following webpages:
Animations at Physics Classroom
Simulation of projectile motion at PhET
Next time we will get into circular motion!
Bye!
