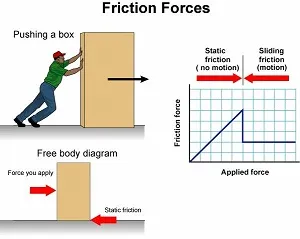
Hello it's a me again! Today we continue with Physics by covering some examples in the topic of contact forces and friction. If you don't know what contact forces and friction are or how to solve newton law exercises in general I suggest you to read the following of my posts:
If you are interested you can find my previous post about of 1st and 2nd law examples here.
So, without further do, let's get started!
Example 1:
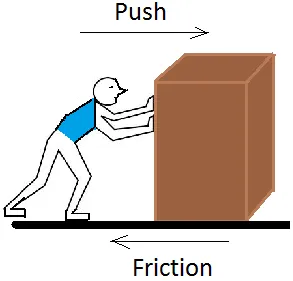
A worker pushes a small 9 kg box on a horizontal plane with a constant velocity of 5 m/s. Suppose that the kinetic friction factor (μk) is 0.2 and that the earth's gravity is 10 m/s^2.
Calculate:
a) the horizontal force that the worker applies so that the (constant) motion continues.
b) the time that it will take for the box to stop (standstill time) if the worker stop's pushing.
a)
Because we have a constant linear motion the 1st law applies.
The only forces applied are:
- friction and worker force horizontally
- weight and ground force vertically
That way the ground force N equals the weight W = mg = 9*10 = 90 N.
Horizontally we have:
ΣF = 0 =>F - T = 0=> F = T =>
F = μk * N => F = 0.2 * 90 => F = 18 N
b)
The friction T is equal to the worker's force and so the deceleration can be found by the 2nd law.
F = T = ma => 18 = 9 * a => a = 2m/s^2 backwards
That way from the constant linear acceleration motion equation we have:
u = uo + at =>
o = 5 - 2 * t => 2t = 5 => t = 2.5 seconds
Example 2:
Suppose that we have the same box as in Example 1, but this time it moves with a constant acceleration of 0.2 m/s^2, because of the worker's force. At t = 0 secs the box is standing still. Gravity is g = 10 m/s^2 and μk = 0.2 again.
Calculate:
a) the worker's force (F)
b) the time needed for the box to stop if the worker stops pushing it at t = 10 secs
c) the time of b if we where on the moon that has a gravity of g = 1.6 m/s^2
a)
In Example 1 we calculated that the maximum friction is T = 18 N.
If we didn't knew that than we could also use the following:
Tmax = μk*W = μk*m*g = 0.2*9*10 = 18 N
Because the acceleration is constant we will use Newton's 2nd law.
ΣF = ma => F - T = ma => F - 18 = 9 * 0.2 => F = 19.8 N
b)
After 10 seconds the object will have velocity of:
u = u0 + at => u = 0 + 0.2*10 = 2 m/s
When the worker stops pushing the deceleration will be a = 2m/s^2
(as we calculated in Example 1)
That way the box will stop moving after 1 second that can be found by using:
u = u0 + at => 0 = 2 - 2*t => 2t = 2 => t = 1 sec
c)
Supposing that the worker's force is now less and that the acceleration and max velocity reached also stay the same as before we now have to calculate the new friction.
T = μk * W = μk * m * g = 0.2 * 9 * 1.6 = 2.88 N
By using Newton's second law we can calculate the deceleration.
T = ma => 2.88 = 9 * a => a = 0.32 m/s^2 backwards
Using the same equation as before we can now calculate the stop time.
u = u0 + at => 0 = 2 m/s - 0.32 * t => 0.32 t = 2 => t = 6.25 secs
So, the box would need 5.25 seconds more than on earth!
Example 3:
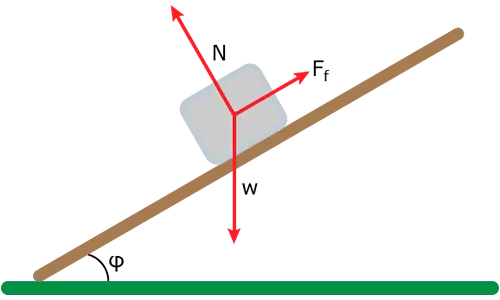
Suppose a box (with mass m) on top of a inclined plane that stands still with a φ angle to the horizontal axis. The kinetic and static friction factors are equal to 0.3 and 0.4 respectively. The gravity g is equal to 10 m/s^2
Calculate:
a) the maximum angle φ for which the box doesn't slide down
b) calculate the box's acceleration for that maximum φ angle
c) the time taken to slide 8 m on top of the inclined plane of maximum φ angle
a)
Analyzing the weight into components we get a parallel to inclined plane force:
Wx = mgsin(φ) = 10msin(φ) (φ and m are unknown)
and the vertical force (equal to N):
Wy = mgcos(φ) = 10mcos(φ) = N
The static friction (Ts) is:
Ts <= μs * N => Ts <= 4mcos(φ)
The exact moment where Ts gets the max value we start sliding.
That way from the 1st law we have:
Ts = Wx => 10msin(φ) = 4mcos(φ) =>
4/10 = tan(φ) => φ = arctan(0.4) => φ ~= 21.7 degrees
b)
The kinetic friction (Tk) equals:
Tk = μk * N = 3mcos(φ)
When the angle is φ = 21.7 degrees (that we calculated from a) we start having kinetic friction and an acceleration and so from the 2nd law we have:
ΣF = Wx - Tk = ma => 10m*sin(φ) - 3mcos(φ) = ma =>
10sin(21.7) - 3cos(21.7) = a => a ~= 0.91 m/s^2
c)
Using the constant linear acceleration equation we get:
x = x0 + u0t + 1/2 at^2 =>
10 = 0 + 0 + 1/2 * 0.91 * t^2 =>
t^2 = 10*2/0.91 => t = root(21.98) =>
t ~= 4.68 secs
Note:
You can see that the mass was not needed in the whole example. This happened (mathematically) because all the terms of the equations contained m and so reduction was possible. This also means that the friction and weight problems with inclined planes don't depend on the mass and that everything has to do with the gravity and friction factors!
Image Sources:



And this is actually it and I hope that you enjoyed it!
Next time we will cover examples in circular motion dynamics.
Bye!
