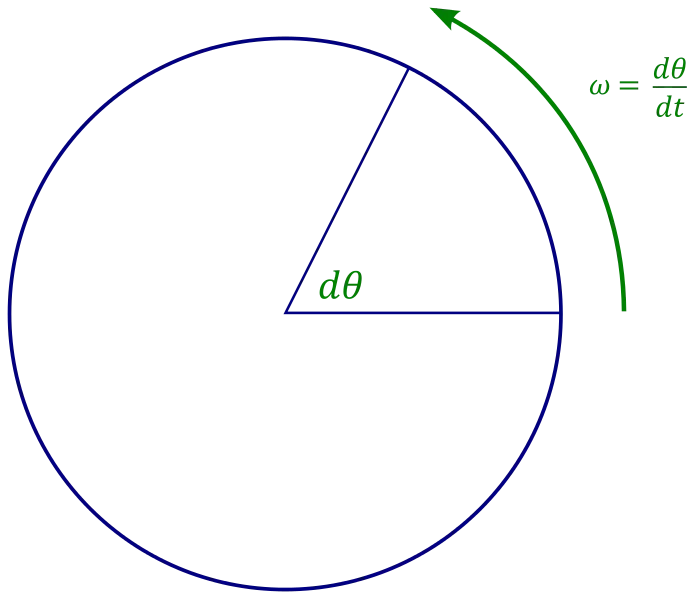
[Image 1]
Introduction
Hey it's a me again @drifter1! Today we continue with Physics and more specifically the branch "Classical Mechanics" to get into Angular motion, giving the basics of how we define position, velocity and acceleration in such motions. I guess that it's worth mentioning that some topics where already covered in circular motion, but we will get into them a little bit more in-depth now. So, without further ado, let's get straight into it!
Angular position
Thinking about the dimensions that motion takes place, we can talk about:- straight-line or linear motion, where a particle moves along one axis
- plane motion, where a particle moves along two axes (e.g. xy-plane)
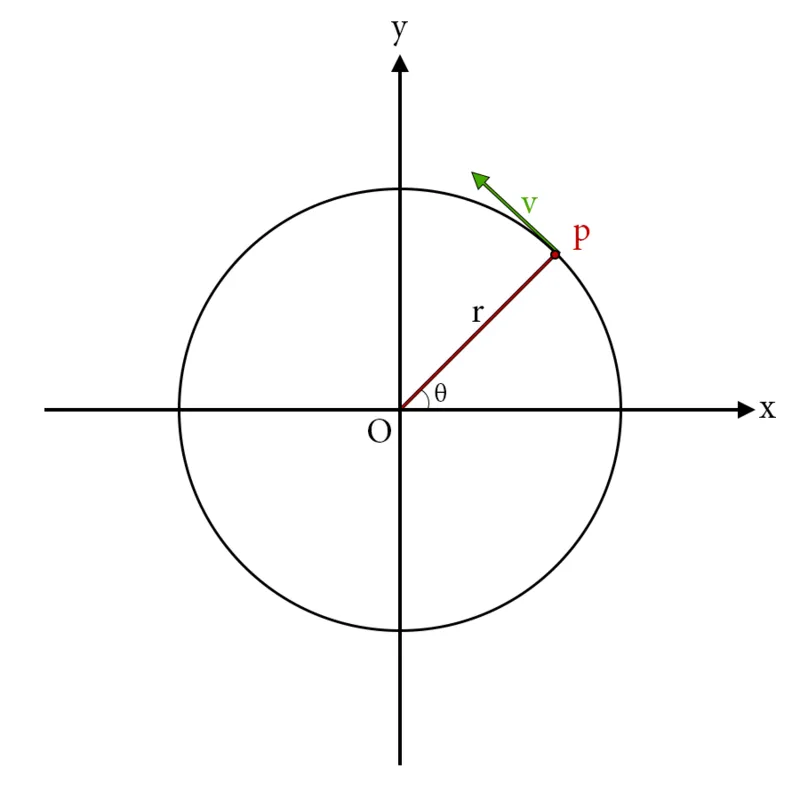
[Based on Figure 1 from physicskey.com]
Let's consider the upper Figure, where a particle moves along the circle with a velocity v and being at the point p(x, y). The position of the particle can also be described by the angular angle θ that is measured from above the positive x-axis. So, clockwise rotation along the circle is considered to be negative and anti-clockwise to be positive. To know the direction we just have to find the angle difference Δθ.
The angle difference can also be calculated knowing the arc length Δs of the motion (part of the circumference a particle travelled) and radius r of the circle:

So, in the end the position of the particle is determined by the angular angle θ.
Angular velocity
In angular motions, velocity is defined as the angular displacement over time. So, if θ1 is the angular displacement/position at some time t1 and θ2 the angular displacement at time t2, the average angular velocity is: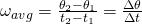
As you can see, the angular velocity is denoted by the Greek letter "ω" (omega). It's calculated in rad/sec, based on the angle unit of Radians (2π rad = circle) and the time unit of Seconds. Thinking about instantaneous angular velocity, we have to let the time interval Δt approach zero. This gives us:
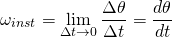
Angular velocity is determined by the right hand rule, where you have to curl the fingers of your right hand in the direction of rotation, leaving the thumb straight along the z-axis or perpendicular along the plane of rotation (xy-plane in our case). The thumb gives us the direction. If the particle moves clockwise, the angular velocity "goes upward". In the case of anti-clockwise motion, the angular velocity will "go into the page".
Thinking about the angle, radius and arc length, we can write:
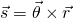
Doing some calculations using this equation, we can end up with the following equation that gives us the tangential speed of the particle, using the radius and angular velocity:
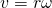
Let's also write the vector-form of this equation:
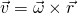
This equation, shows us why the angular velocity is in the third dimension...
Angular acceleration
As always acceleration defines the change in speed over time. So, in this case, angular acceleration is defined as the change in angular velocity over time: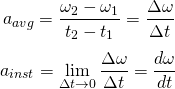
To find the direction of angular acceleration, you can't use the right hand thumb rule of before. Here you have to find the difference of the angular velocities. So, if the particle's linear speed increases (in clockwise or anti-clockwise direction) then the angular velocity and acceleration lie in the same direction. If the linear speed decreases then the angular velocity and acceleration lie in opposite directions.
The centripetal (towards the centre) and tangential acceleration of the particle can be calculated using the following equations, that can be proven using the previous equations of velocity:

RESOURCES:
References
- https://www.physicskey.com/20/angular-position-velocity-and-acceleration
- https://courses.lumenlearning.com/boundless-physics/chapter/velocity-acceleration-and-force/
- https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_I_-_Mechanics%2C_Sound%2C_Oscillations%2C_and_Waves_(OpenStax)/10%3A_Fixed-Axis_Rotation__Introduction/10.1%3A_Rotational_Variables
Images

- https://www.physicskey.com/20/angular-position-velocity-and-acceleration
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
- Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
- Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
- Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
- Potential Energy Diagrams -> Internal Energy, Internal Work
Momentum and Impulse
- Conservation of Momentum -> Momentum, Conservation of Momentum
- Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
- Collision Examples -> Various Elastic and Inelastic Collision Examples
- Impulse -> Impulse with Example
- Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
- Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis
Final words | Next up
This is actually it for today's post! Next time we will start getting into the rotation of objects, starting off with angular velocity and acceleration...
See ya!


Keep on drifting!
