
[Image 1]
Introduction
Hey it's a me again @drifter1! Today we continue with Physics and more specifically the branch "Classical Mechanics" to get into Angular Momentum and it's Conservation. So, without further ado, let's get straight into it!
Angular Momentum
Similarly to how we defined momentum for Translational motion (p = m·v), we also define a different kind of momentum, called Angular Momentum, for Angular motion! This quantity characterizes the rotary inertia of an object or system of objects that's rotating about an axis. It's symbolized by the capital letter 'L'. Thinking about the relationship of angular and linear motion, we can also define angular momentum as the product of linear momentum times the perpendicular distance from the axis of rotation:
Substituting p with it's corresponding part m·v we get
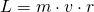
Knowing that the tangential velocity can be written in respect to angular velocity as v = ω·r we can substitute v to obtain:

The first part corresponds to the moment of inertia I and so we finally have:
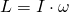
We can see that angular momentum is calculated in Kg · m2/s. Of course, Angular momentum is a vector quantity pointing in the same direction as the angular velocity. Furthermore, notice that this equation tells us that objects with large moments of inertia (Ex. Earth) or large angular velocity (Ex. centrifuge) have a very large angular momentum! Quite useful to know :)
Conservation of Angular Momentum
Similar to linear momentum, angular momentum is also being conserved! As long as no external torque acts on a system (net τ = 0), the total angular momentum of the system remains constant. Which means that I·ω = constant. From the article about torque and it's connection to angular acceleration we have:
Substituting a with the equation that connects it with ω (a = dω/dt) we have:

So, the torque acting on a system is equal to the rate of change of angular momentum. When no external torque acts on the system (τ = 0) we have:

Which shows us that the angular momentum in some state 1 is equal to the angular momentum in some state 2, because the angular momentum remain constant (dL/dt = 0).
Again no examples today, as examples around the whole topic of angular motion will come in a follow-up article ;)
RESOURCES:
References
- https://www.britannica.com/science/angular-momentum
- https://www.sciencetopia.net/physics/angular-momentum-principles
- https://opentextbc.ca/physicstestbook2/chapter/angular-momentum-and-its-conservation/
Images
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, acceleration and averages of those
- Rectlinear motion with constant acceleration and free falling -> const acceleration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and acceleration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
- Force and Potential Energy -> Force as Energy Derivative (1-dim) and Gradient (3-dim)
- Potential Energy Diagrams -> Energy Diagram Interpretation, Steps and Example
- Internal Energy and Work -> Internal Energy, Internal Work
Momentum and Impulse
- Conservation of Momentum -> Momentum, Conservation of Momentum
- Elastic and Inelastic Collisions -> Collision, Elastic Collision, Inelastic Collision
- Collision Examples -> Various Elastic and Inelastic Collision Examples
- Impulse -> Impulse with Example
- Motion of the Center of Mass -> Center of Mass, Motion analysis with examples
- Explaining the Physics behind Rocket Propulsion -> Required Background, Rocket Propulsion Analysis
Angular Motion
- Angular motion basics -> Angular position, velocity and acceleration
- Rotation with constant angular acceleration -> Constant angular acceleration, Example
- Rotational Kinetic Energy & Moment of Inertia -> Rotational kinetic energy, Moment of Inertia
- Parallel Axis Theorem -> Parallel axis theorem with example
- Torque and Angular Acceleration -> Torque, Relation to Angular Acceleration, Example
- Rotation about a moving axis (Rolling motion) -> Fixed and moving axis rotation
- Work and Power in Angular Motion -> Work, Work-Energy Theorem, Power
Final words | Next up
And this is actually it for today's post! Next time we will explain the Physics of Gyroscopes...
See ya!


Keep on drifting!

