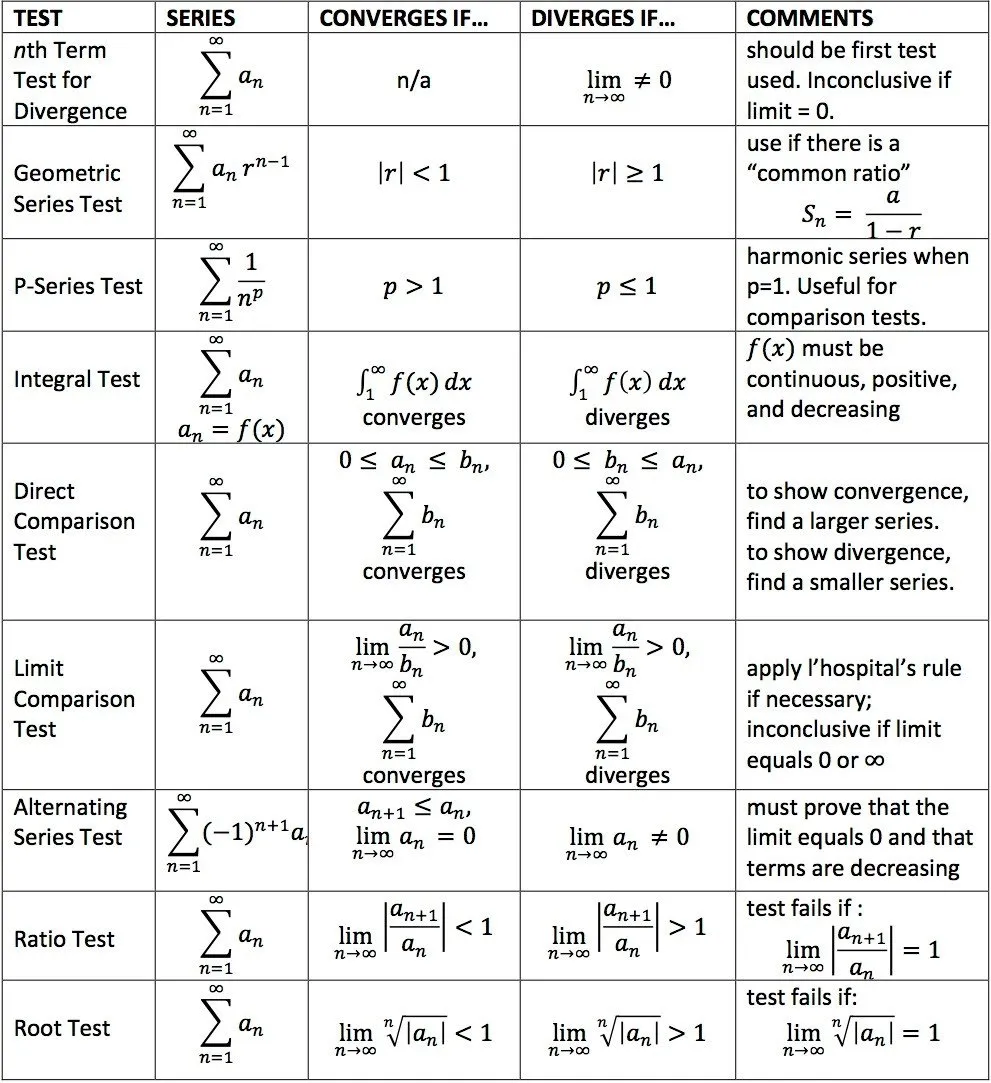
Hello it's me again drifter1! Today we continue with Mathematical Analysis getting into more about Series. After talking about the Basics in my last post here, we will now get into how we test the Convergence. So, without further do, let's get started!
Cauchy's Convergence Criterion:
A Series s converges only when for every e>0 there is a natural number n0 such that:
|S| < e => |a(n) + a(n+1) + ... + a(n+m)| < e for every m, n with m>=n>n0
We can also describe it as:
- for every e>0 there is a natural n0 such that |Sm - Sn| < e for every m, n with m>=n>n0
- for every e>0 there are natural p, n0<=n such that |S(n+p) - Sn| < e <=> lim n->∞ (S(n+p) - Sn) = 0
Example proof:
Using this Criterion we can easily proof that the harmonic series with p=1 (1/n terms) diverges.
For m = 2n there is a n0 so that for every e>0 and n>=n0: |S2n - Sn| < e
The generic term of such a series is a(n) = 1/n and so:
S2n - Sn = 1/n+1 + 2/n+2 + ... + n/2n > n/2n = 1/2 => |S2n - Sn| >= 1/2.
And so Cauchy's criterion is not true and the series diverges.
So, where does this help us?
Well, think about the limit of (an) as a testing method of convergence.
- When the series converges then the lim n->∞ (an) = 0
- If lim n->∞(an) !=0 then the series diverges
ATTENTION: It doesn't mean that a sequence converges when the limit is 0, but if it isn't 0 then we are 100% sure that the series diverges. Think about the harmonic series from before, where the limit of 1/n to infinity is equal to 0, but the series diverges!
Sequence Boundary Test:
Suppose s is positive series (an >=0 for every natural n).
- s converges only if the sum of n-terms (sn = a1 + a2 + ...+ an) is bounded
- s diverges if the sum of n-terms (sn = a1 + a2 + ...+ an) is not-bounded
Comparison Test:
Suppose s1 and s2 are two positive series with terms an and bn and 0 <= an <= bn for every natural n.
- If s2 converges then s1 converges also
- If s2 diverges to ∞ then s1 also diverges to ∞
This means that we can check the convergence/divergence of a "greater" series to check the convergence/divergence of a "smaller" series.
Series Addition Convergence:
Suppose the Series s1, s2 with terms an, bn and the real numbers k, l. If the series converge to a and b respectively then the series S with term k*an + l*bn converges to k*a + l*b.
Cases:
- If both converge then the result series S also converges
- If at least one diverges then the result series S also diverges
So, in a sum of Series, if at least one diverges then the whole result also diverges!
Condensation Test:
Suppose (an) is a decreasing positive sequence (an>=an+1>=0).
- The series with term (an) converges only if the series with term 2^k*a(2^k) converges and vise versa
- In the same way if one diverges then the other diverges too
Application:
Let's talk about harmonic series of p-degree with p being a real number and terms 1/n^p.
- The series converges when p>1
- The series diverges to +∞ when p<=1
This can be proven easily using the condensation test.
For p<=0 we get a series with terms n^k, with k =-p and so the series diverges to +∞.
For p>0 and using the condensation test we check the convergence of the series with term:
2^k/(2^k)^p = 2^(1-p)^k = x^k, where x^k is a geometric series and so we have that:
The series converges when: 2^(1-p) < 1 = 2^0 => p > 1
The series diverges when: 2^(1-p) >= 1 = 2^0 => p <= 1
We know that the first series also converges/diverges for the same values, because of the condensation convergence test.
Limit comparison test:
Suppose the series s1, s2 with positive terms an and bn and the limit n->∞ (an/bn) = k.
- If 0 < k < + ∞ then s1 and s2 converge/diverge together
- If k = 0 then if s2 converges then s1 also converges (NOT vise versa)
- If k = +∞ then if s1 converges then s2 also converges (NOT vise versa)
This is pretty useful in series build up of polynomial sequences.
Ratio test:
Suppose s is a non-zero series with term (an) and lim n->∞|a(n+1)/an| = l, with l > 0.
- If l < 1 then the series converges
- If l > 1 then the series diverges to +∞ and lim n->∞ (an) != 0
- If l =1 then we don't know and need to use some other test.
This one is pretty useful when having a rational term build up of exponentials, factorials and more.
n-root Test:
Suppose s a series with term (an) and lim n->∞ [n-root(|an|)] = l, with l > 0.
- If 0 <= l < 1 then the series converges
- If l > 1 then the series diverges to +∞
- If l = 1 then we don't know and need to use some other test.
This one is pretty useful in series build up of polynomial sequences to get rid of high exponentials.
Absolute test:
When s is a Series build up of terms (an) and |s| is a sereis build up of terms |(an)| then:
- If |s| converges then s also converges, but the opposite is not true!
- We don't know about divergence
Integral test:
Suppose a integratable, positive and increasing function f:[1, +∞) -> R.
The definite integral:
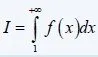
and the Series:
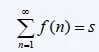
converge/diverge together.
When their converge then we know that I < s < I + f(1) with I:
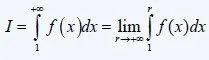
Leibniz Criterion for Alternating Series:
When the absolute value of the terms of an alternating series are a decreasing and null-sequence then the series converges.
So, for an alternating series with term (-1)^(n+1) * (an) we have that it converges when:
- a(n) >= a(n+1) >= 0 for every natural n
- lim n->∞ (an) = 0
Sum/Limit approximation:
When such a series converges then we can calculate the limit approximately.
The sum of n-terms is: a1 - a2 + a3 - ... + (-1)^(n+1)*(an).
This value comes close to the sum of our series s having an error.
The value of this error is smaller then the absolute value of the (n+1)-term: |s - Sn| <= an+1
The remainder (s-Sn) has the same sign as the (n+1)-term.
And this is actually it for today and I hope you learned something!
The post would become too clumped up if I also put Examples for everything today. That's why we will get into examples for all (or some) of the convergence tests we covered today in my next post.
Until next time...Bye!
