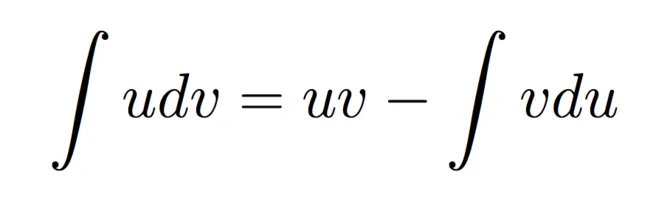
Hello its me again drifter1! Today we continue with Mathematical Analysis getting into another Integration Technique! The Integration by parts technique is used a lot of times and mostly is simple to use, but there are also some cases where it becomes more difficult. You can check out my previous post about the Substitution Technique here.  So, without further do let's get started! 

Integration by Parts:

    This type of integration is used when we have a product of functions inside of the integral. We try to transform this product so that one of the two parts is an derivative and the other an antiderivative (the function itself) and then we use a product-like differentiation.

This looks like this:

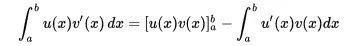
where u, v are functions inside of the integral and v is differentiated.

     Then we have to take the value of u*v from a -> b, as we would if it was an Definite Integral and substract this value from a new integral that has the differentiations in opposite way (u is now differentiated and v not).

So, using this technique we transform our uv'dx integral into an u'vdx integral.

     The choice of which one of the two functions we tranform into an derivative is important and we mostly can choice either one of those, but sometimes it's faster to solve in one way or some way may not give us a solution. We will get into which one we chose depending on the type of functions that we have inside of the integral.

So, let's get into some common cases so that you understand the way we have to think.

Integrals with Polynomial and Trigonometric Functions:

Suppose we have the integral:

We know that cos(x) = [sin(x)]' and so we will use this to solve the integral.

So, we have integral[x*(sin(x))'dx] = xsin(x) - integral[x'*(sin(x))dx] = xsin(x) - integral[sin(x)dx]

The last one is one of the basic integrals and so we end up with:

integral[xcos(x)dx] = xsin(x) + cos(x) + c, where c a real number.

    

    If we solve using x = (x^2/2)' we will see that the power's of x will increase recursively and so we will do the same thing over and over again and the integral will never be solved!

    So, whenever we have polynomials and trigonometric functions we chose to differentiate the trigonometric function!

Integrals with Polynomial and Exponential Functions:

Suppose we have the integral:

We know that e^x = (e^x)' and so we will use this to solve the integral.

So, we have integral[x^2*(e^x)'dx] = x^2*e^x - integral[(x^2)'*e^xdx]

= x^2*e^x - integral[2*x*e^xdx]

You can see that using e^x we decreased the power of the polynomial from 2 to 1.

So, let's do it again!

Then we have x^2*e^x - integral[2*x*(e^x)'dx] = x^2*e^x -{2*x*e^x - integral[(2x)'*e^xdx] }

= x^2*e^x - 2*x*e^x + integral(2*e^xdx).

This last one is a simple integral that gives us 2*e^x and so our final result is:

integral[x^2*e^xdx] = x^2*e^x - 2*x*e^x + 2*e^x +c, where c a real number

    If we chose to differentiate the polynomial x^2 = (x^3/3)' we will again have the power be increased in every step and e^x will stay the same! This means that we will recursively never solve the integral.

    So, whenever you have polynomials and exponential functions chose to differentiate the exponential function and not the polynomial.

Integrals with Polynomial and Logarithmic Functions:

Suppose we have the integral:

Let's chose to differentiate with x = (x^2/2)' this time.

We have that integral[(x^2/2)'*lnxdx] = (x^2/2)*lnx - integral[x^2/2*(lnx)'dx]

    We know that (lnx)' = 1/x and so we see that the logarithmic function will disappear and that the polynomial will return to it's first power that was 1.

So, our final result is:

integral[x*lnxdx] = (x^2/2)*lnx - 1/4*x^2 + c, where c is a real number

    We can solve it using the logarithmic function, but we will increase the power of the logarithm if we chose lnx = [(lnx)^2/2]' and eliminate the polynomial that way. The problem is that we then end up with an logarithm and have to apply the technique that I will cover lastly today and this takes to much time.

    So, whenever we have a polynomial and logarithmic function we chose to differentiate the polynomial function! This is actually also the only time that we chose to differentiate the polynomial.

Integrals with Exponential and Trigonometric Functions:

Suppose we have the integral:

Here we can chose to differentiate either one of those and there will not be any change at all.

Let's choose cos(x) = [sin(x)]'

We have that I = integral[e^x*cos(x)dx] = integral[e^x (sin(x))'dx]

= e^x*sin(x) - integral[(e^x)'*sin(x)dx]

Let's now chose to differentiate with sin(x) = [-cos(x)]'

e^x*sin(x) - integral[e^x*(-cos(x))'dx] = e^x*sin(x) - {e^x*(-cos(x)) - integral[(e^x)'*(-cos(x))dx]

= e^x*sin(x)  +e^x*cos(x) - integral[e^x(cos(x)]dx.

Hmm, we see that we follow a pattern and that integral I has reappeared.

This means that I = e^x*sin(x) + e^x*cos(x) - I => 2I = e^x(sin(x) + cos(x)) =>

I = 1/2 * e^x(sin(x) + cos(x)) + c, where c a real number.

The same result can be found by using e^x = (e^x)'.

    So, whenever we have integrals with exponential and trigonometric functions we chose either one of those and try to find a pattern (the first integral) that reappeared so that we solve a little equation to find the integral we want!

Functions multiplied with x' = 1 (unity):

Suppose we have the integral:

    This integral is not in an known form and so we will use this new technique where we multiply with x' that equals 1 or unity as some like to call it!

So, we have that integral[x'*arctan(2x)dx] = x*arctan(2x) - integral[x*(arctan(2x))'dx]

We know that (arctan(x))' = 1/1+x^2 and so here we have a composition case where:

[arctan(2x)]' = (2x)'/1+(2x)^2 = 2/1+4x^2

This means that we now have:

x*arctan(2x) - integral[2x/(1+4x^2)dx]

If you look closely you will see that this is actually as simple integral case for ln|f(x)|.

So, 2x can be written as 1/4*(1+4x^2)' and we have:

x*arctan(2x) - 1/4*integral[(1+4x^2)'/(1+4x^2)dx] =

x*arctan(2x) - 1/4* ln(1+4x^2) + c, where c a real number.

    So, whenever we have some function that is not a known case we also try the product with x' to see if we get a result. 

Try solving the following integral using this last technique:

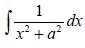
The answer you need to get is: 

    Something that we can also get using the substitution technique for integrals that contain a^2*x^2 + b^2, where b is now a, from last time. We will have to set x = atan(t) => t = tan-1(x/a) and so on...

    So, I hope that you now understood the way that we have to think about product integrals or even single integrals that can't be solved directly! If you have some other form that is a product just try differentiating one of the two functions first and if it doesn't work out try the other way around. Sometimes you may see that it can't be solved using this technique and then you might need to use the substitution technique or some other technique that may be better suited for this type of integral you are trying to solve.

And this is actually it for today and I hope you enjoyed it!

The next techniques that I will cover in our series will be about solving rational integrals.

Bye!