Hello its me Drifter Programming! Today we continue with Mathematical Analysis, getting into some more stuff about Functions. We will talk about Monotony, Extrema etc. and lastly also get into some Categories or Types of Functions. It would be good to check out our last post about Functions first. So, without further do let's get straight into it!

Function Monotony:

Suppose a function f: A -> R and B a subset of R.

• f is increasing in B, when for every x1, x2 in B with x1 < x2 implies that f(x1) <= f(x2). f ↑
• f is strictly increasing in B when for every x1. x2 in B with x1 < x2 implies that f(x1) < f(x2).
• f is decreasing in B, when for every x1, x2 in B with x1 < x2 implies that f(x1) >= f(x2). f↓ 
• f is strictly decreasing in B when for every x1. x2 in B with x1 < x2 implies that f(x1) > f(x2).
• f is called a (strictly) monotonic function when it is (strictly) increasing or (strictly) decreasing.

With all that we have that:

1. When f is increasing and decreasing in B at the same time, well that is is a constant function (f(x) = c)
2. When f is strictly monotonic in B it is also bounded in B and 1-1 (1-1 doesn't mean it is also strictly monotonic tho)
3. When f is strictly monotonic (increasing or decreasing) then the inverse function f^-1 is also strictly monotonic (increasing or decreasing)
4. To find out the monotonicity we use the division of change λ = (f(x2) - f(x1)) / (x2 - x2).

• λ > 0 => f is strictly increasing
• λ >= 0 => f is increasing
• λ < 0 => f is strictly decreasing
• λ <= 0 => f is decreasing
• λ = 0 => f is constant

Example:

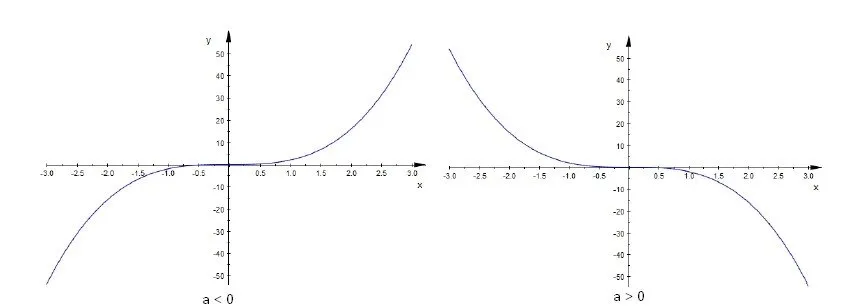
Suppose the function f(x) = a*x^3, with a != 0.

1. When a > 0, f is strictly increasing
2. When a < 0, f is strictly decreasing
3. Function f is 1-1, cause it is strictly monotonic in R.

Extrema:

Suppose function f: A -> R.

• when there is a x0 in A so that for every x in A we have that f(x) <= f(x0) then x0 is called the global maximum of f. The position x0 is called the maximum value of f.
• when there is a x0 in A so that for every x in A we have that f(x) >= f(x0) then x0 is called the global minimum of f. The position x0 is called the minimum value of f.
• the global maximum and minimum are called the global extrema of f.
• when there is a x0 in A so that for every x in a subdivision of A we have that f(x) <= f(x0) then x0 is called a local maximum of f.
• when there is a x0 in A so that for every x in a subdivision of A we have that f(x) >= f(x0) then x0 is called a local minimum of f.

Example:

Suppose f: A -> R, with f(x) = x^2 - 4x + 4.

xo = 2 is the global minimum of f with f(2) = 0.

We know this, cause f is strictly decreasing in (-∞, 2] and strictly increasing in [2, +∞).

(We will get into how we find this out posts later on)

Function Categories:

Linear Function [f(x) = a*x + b]:

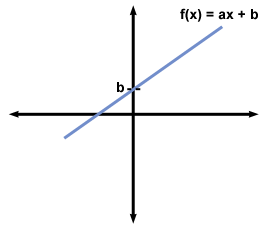
• The Graph of f contains all the points in 2d space for which y = a*x + b and so is a line ε
• The line ε intersects with the x axis in the point A(-b/a, 0
• The line ε intersects with the y axis in the point B(0, b)
• a = tan(ω) = y2 - y1 / x2 - x1 is called the slope of f
• With a = 0 we have a constant function f(x) = b that is parallel to the x axis

Parabola Function [f(x) = a*x^2 + b*x + c, where a!=0]:

• The parabola is intersecting with the y axis in the point A(0, c)
• The parabola is intersecting with the x axis depending on the discriminant's sign (Δ = b^2 - 4*a*c)
• When Δ > 0 the parabola is intersecting in two points X1( (-b -root(Δ))/2*a ,0) and X2( (-b +root(Δ))/2*a ,0)
• When Δ = 0 the parabola is intersecting in one point X(-b/2*a, 0
• When Δ < 0 the parabola is not intersecting with the x axis.
• The vertex of the parabola is at the position C(-b/2*a, -Δ/4*a)
• The convexity of the parabola depends on the sign of a (or mostly called p)
• When a>0 then the parabola is concave (or surfaces curve inwards)
• When a<0 then the parabola is convex (or surfaces curve outwards)
• The curvature of the parabola depends on the sign and the value of a

Here you can see how the value of a affects the different parabola functions:

Cubic Function [f(x) = a*x^3, where a!=0]:

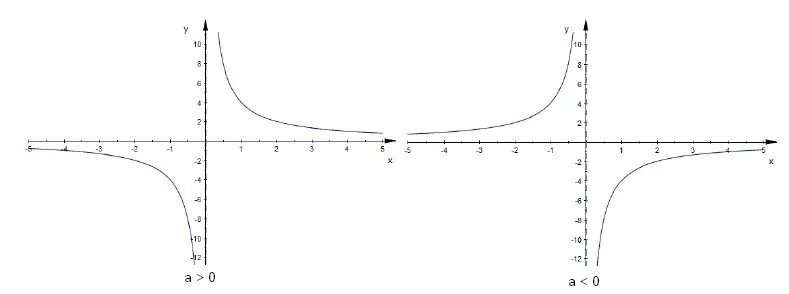
Hyperbola Function [y = a/x, where a!=0]:

Exponential Function [f(x) = a^x, where a> 0]:

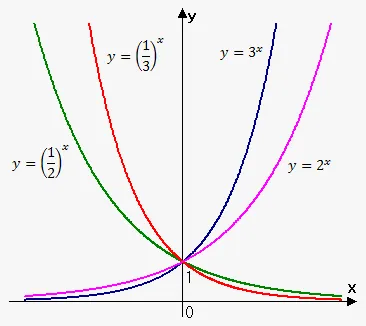
• For a > 1 the function is strictly increasing
• For 0 < a < 1 the function is strictly decreasing
• For a = 1 the function is constant and equal to 1 (1^x = 1)
• Any exponential function is strictly monotonic

Logarithmic function [f(x) = loga(x), where x, a > 0]:

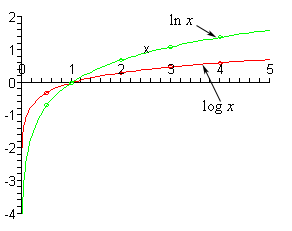
• loga(x) = y <=> x = a^y, where a is called the basis
• When a = 10 we have log10 that is called a common logarithm
• When a = e = 2,718... we have ln that is called the natural logarithm
• Any logarithmic function is strictly monotonic
• A logarithmic function is the inverse of an exponential function

Properties:

Trigonometric Functions:

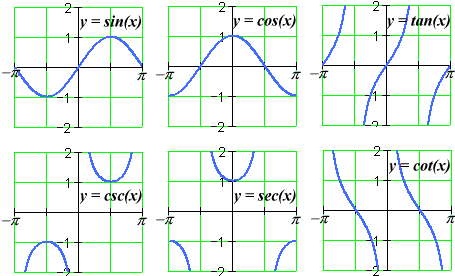
• You can read about trigonometric functions here in wikipedia
• You should know sin(x), cos(x), tan(x), cot(x) and the arc's (inverse functions) of them
• Here a list of trigonometric identities/rules from which we will need some later on

Hyperbolic (Trigonometric)Functions:

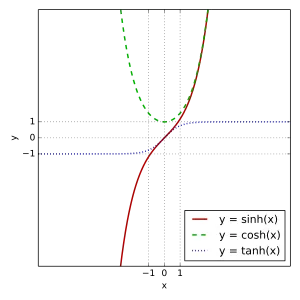
• You can read about hyperbolic function here in wikipedia
• You should know the sinh(x), cosh(x), tanh(x) and coth(x) and the inverses of them.
• You can also check out some of the identities/relations/formulas, cause we will may need them posts later on.

And this is actually it and I hope you enjoyed it!

Next time we will get into Limits and Continuity...

Bye!