Hello it's me again. Today we will talk about another way of getting an simplified circuit function and so an circuit. This simplification method uses the so called Karnaugh Maps and today's post will get into everything you need to know about them. So, let's get started!
Introduction:
Karnaugh maps represent logical functions and so truth tables. A Karnaugh Map is an array were each square/element of it represents an combination of variables, so each square with value of 1 represents an minterm and each square with 0 represents an maxterm of our logical function! We can group those 1's or 0's (preferable 1's) and make our function the simplest possible.
A Karnaugh Map is an array and we mostly use 2, 3 and 4-Variable K-Maps. After that another method called Quine McCluskey is used much easier (we will talk about it much later).
We will put the Output Values of our Logical Circuit Function in the corresponding square of the K-Map using some tricks that I show you in the Examples Section!
K-Map Rules:
Let's now get into Rules that apply, so that we then get into some examples in all 3 Types. The Rules are simple to remember and after some examples you should be doing K-Map like an expert!
So, The Rules are:
- Only one Variable changes when we go to the left-right or to the top-bottom from any square (that applies to the way we set up the values of the Inputs, when creating our K-Map)
- Each square represents an Minterm or Maxterm (we mostly use Minterms)
- We put values of 0 or 1 inside the squares, that represent the output when having the Input values that this specific square represents (that's why we use Minterms, cause we can use the Outputs as they are in our Truth Table)
- We can group only squares in powers of 2 (1, 2, 4 ,8, 16, ...)
- We try to find the largest and so minimal groups
- Groups need to be Vertical, Horizontal Grouped or be Squares-Rectangles and we do not group Diagonally
- Groups can overlap the square (so an item from the top-left can group with an item from the top-right to form a group of 2 and even all the corners could be grouped into one group of 4)
- A Group is represented as a Minterm represenation inside of our Function.
- The Variables inside of a group that change values inside of the group get left out of the group's Minterm representation.
- The Variables will be put as is when they have a value of 1 and with an NOT symbol (') when they have a value of 0.
Examples:
Let's now get into some Examples that will show you what I mean!
2-Variable K-Map:
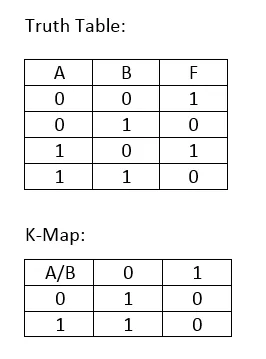
From the top Truth Table I created the K-Map and now we have to Group the 1's. There is only one Vertical Group and in that group only B doesn't change value (always 0). So, the representation of our Function is:
F(A, B) = B'
3-Variable K-Map:
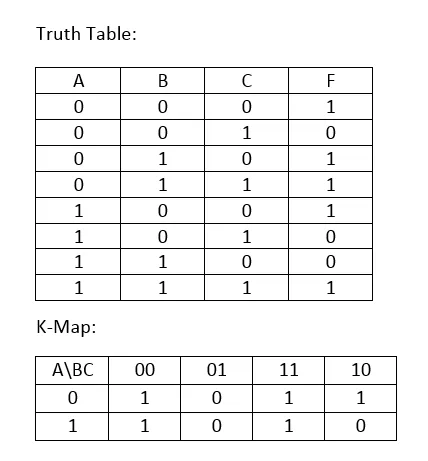
From the top Truth Table I created the K-Map. An easy way of putting the values is that we take the values as they are in the Truth Table and switch places of the last two in each row.
Now, we can create many different kinds of groups! The problem is that we can't create any group of 4 so, we will end up with 2 groups of 2 and 1 group of 1! Which ones you take is up to you.
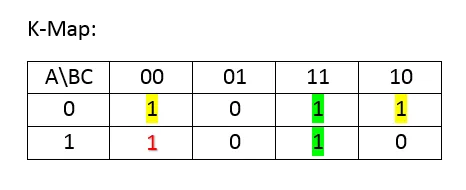
I took those "3" Groups. The Red one is alone (and lonely), the Yellow one is an overlapping Horizontal Group of 2 and the Green one an Vertical Group of 2. The Red one is an Minterm and so we put all of the Variables as is.
So, Red looks like this: AB'C'. In the Yellow one only B changes value and so we leave it out and our group looks like this: A'C'. In the Green Group A changes value and so we leave it out and our group looks like this: BC.
Finally our function is the sum of those 3:
F(A, B, C) = AB'C' + A'C' + BC
We could simplify it a little bit more if we take C' as an common factor of the first two. So, we end up with:
F(A, B, C) = C'(AB' + A') + BC
I also don't like that we have so many NOT's so I will use the De Morgan Theorem on the first part:
F(A, B, C) = [C + (A'+B)A]' + BC
That's our final function!
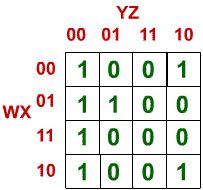
4-Variable K-Map:
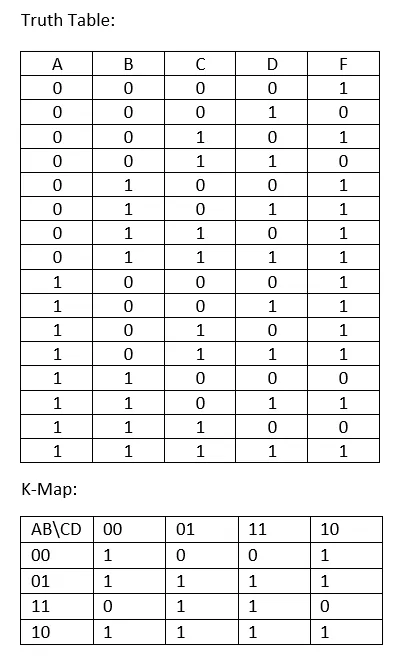
From the top Truth Table I created the K-Map. The way I put them fast inside of the K-Map is similar to the way we used in 3-Variable K-Maps. I put them as I take them from the Truth Table and switch places of the last two in each row and the last two rows also switch places!
Now, we can create again many groups! We can create 3 Groups of 4! And you can do it in 2 Ways (as is saw quickly). Let's make both and compare the functions that will come out of them!
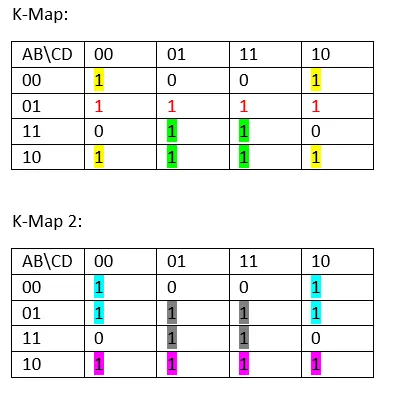
In the first one we took the Corners (square that overlaps!), one Horizontal group of 4 and an Square. In the second one we took an overlapping square, an normal square an and Horizontal group of 4!
Function 1:
- In Group Yellow only B and D don't change values and so the group is: B'D'
- In Group Red only A and B don't change values and so the group is: A'B
- In Group Green only A and D don't change values and so the group is: AD
So, the function is: F(A, B, C, D) = B'D' + A'B + AD
Function 2:
- In Group Grey only B and D don't change values and so the group is: BD
- In Group Pink only A and B don't change values and so the group is: AB'
- In Group Indigo only A and D don't change values and so the group is: A'D'
So, the function is: F(A, B, C, D) = BD + AB' + A'D'
We actually end up with almost the same function but the variables have opposite NOTation (saw what I did there xD). But, both represent the same logic circuit and the same Truth Table, cause they have the same Outputs with the same Inputs, cause they were created from the same K-Map!
It doesn't always look that way! And we could also get an completely different Function, creating our K-Map with different Groups! What is important is that we have the smallest number of Groups possible and that those groups are the biggest we can have!
So, that is the end of today's post. Hope you enjoyed it!
Next time we will get into Basic Logic Gates and after that into Universal Logic Gates and how useful they are!
Until next time..Bye!
