
Hoooola a todos!
Desde que comenzó la pandemia, todos hemos tenido que pasar a la modalidad telemática para poder seguir avanzando en el mundo educativo.
Esta modalidad les ha traído ciertas dificultades a los padres, puesto que se han visto en la necesidad de ayudar a sus hijos con las diferentes materias que ven, muchas veces sin tener los conocimientos necesarios.
Por esa razón, he decidido emprender esta serie de blogs para la comunidad de Hive, en los cuales explicaré lo más detalladamente posible los diferentes temas que los jóvenes pueden ver en la secundaria, haciendo uso de toques de humor que espero les hagan más entretenida la lectura y el aprendizaje, porque aceptémoslo, las matemáticas se pueden tornar muy aburridas.
En este primer tema, abordaremos las potencias y sus propiedades, pero primero es necesario responder: ¿qué es una potencia?

Hellooooo everyone!
Since the pandemic began, we have all had to switch to telematics in order to continue advancing in the educational world.
This modality has brought about certain difficulties for parents, since they have seen the need to help their children with the different subjects they see, many times without having the necessary knowledge.
For that reason, I have decided to undertake this series of blogs for the Hive community, in which I will explain in as much detail as possible the different topics that young people can see in high school, using touches of humor that I hope will make the experience more entertaining. Reading and learning, because let's face it, math can get very boring.
In this first topic, we will address powers and their properties, but first it is necessary to answer: what is a power?
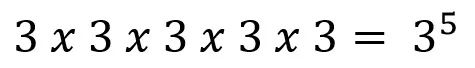
Una potencia es una forma de escribir una expresión algebraica que se multiplica a sí misma tantas veces como se indique, es decir, es una forma de resumir números.
En el siguiente ejemplo vemos una sucesión de factores multiplicados resumidos en algo que es más fácil de manejar y de entender
A power is a way of writing an algebraic expression that multiplies itself as many times as indicated, that is, it is a way of summarizing numbers.
In the following example we see a succession of multiplied factors summarized in something that is easier to handle and understand
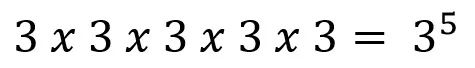
Del lado izquierdo del signo "IGUAL” tenemos un tres que se multiplica a sí mismo cinco veces; una expresión que podemos resumir como se ve del lado derecho del igual: un tres con un cinco pequeñito flotando en la parte superior derecha que indica cuántas veces se va a multiplicar ese tres.
Veamos otro ejemplo:
On the left side of the 'EQUAL' sign we have a three that multiplies itself five times; An expression that we can summarize as seen on the right side of the equal: a three with a tiny five floating in the upper right that indicates how many times that three is going to be multiplied.
Let's look at another example:
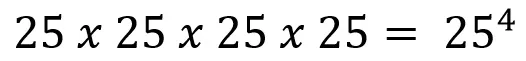
Tenemos un 25 que se multiplica a sí mismo 4 veces, por lo tanto, podemos resumirlo como un 25 con un 4 pequeño flotando a la derecha.
OJO, una potencia puede ser escrita con cualquier cosa que se nos ocurra, a saber, letras y hasta objetos, veamos los siguientes ejemplos:
We have a 25 that multiplies itself 4 times, therefore we can sum it up as a 25 with a small 4 floating to the right.
BEWARE, a power can be written with anything we can think of, namely letters and even objects, let's see the following examples:
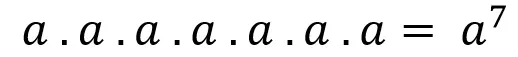

En el primer ejemplo pudimos ver que las letras sirven como factores que se pueden usar en la potenciación (el punto es otra forma de escribir la multiplicación), mientras que en el segundo ejemplo pudimos apreciar que hasta un perro se puede potenciar sin problemas.
Hay que destacar que esta operación se puede hacer en sentido contrario, es decir, lo resumido se puede expandir, por ejemplo:
In the first example we could see that the letters serve as factors that can be used in empowerment (the point is another way of writing multiplication), while in the second example we could see that even a dog can be empowered without problems.
It should be noted that this operation can be done in the opposite direction, that is, the summary can be expanded, for example:
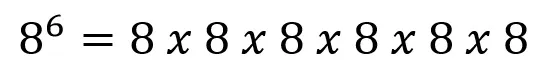
Esto sirve para aclarar un punto importante, y es que el numerito flotante (que ya veremos cómo se llama), nos indica cuántas veces debemos repetir el número grande (que también tiene su nombre).
Ahora bien, veamos cuáles son las partes de una potencia y los nombres correctos que reciben y por los cuales los llamaremos de aquí en adelante
This serves to clarify an important point, and that is that the floating number (which we will see how it is called), tells us how many times we must repeat the large number (which also has its name).
Now, let's see what are the parts of a power and the correct names that they receive and by which we will call them from now on
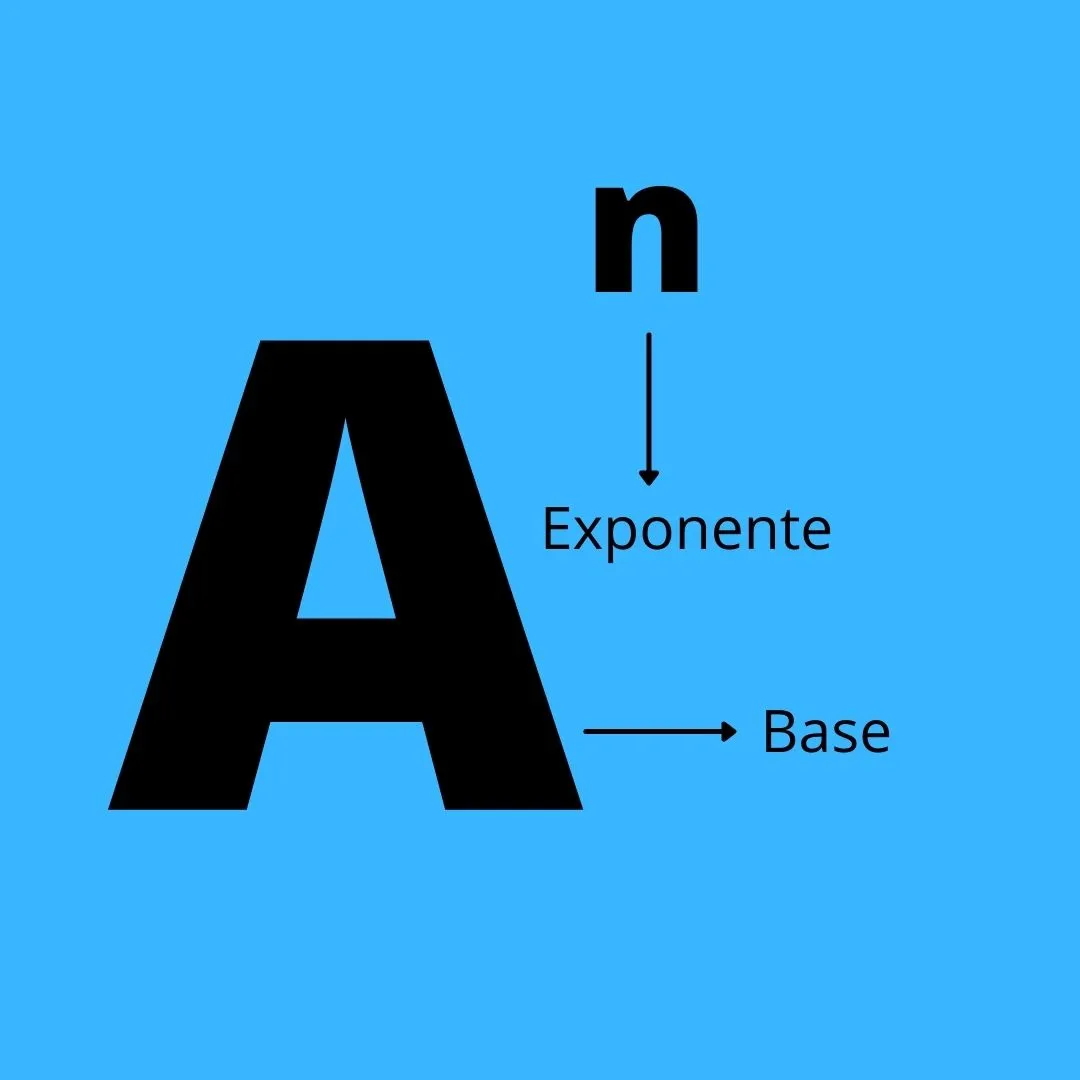
Vemos como el número, letra u objeto grande se denomina “BASE”, y el numerito, letrica o cosita pequeña (porque sí, ahí también puede ir cualquier cosa), se denomina “EXPONENTE”.
Teniendo este nuevo conocimiento, podemos enunciar de una manera más formal lo que es una potencia:
Se trata de una operación matemática donde un factor denominado “BASE” se multiplica tantas veces a sí mismo como lo indique otro factor denominado “EXPONENTE”, y se lee como “a ELEVADO A LA n”.
(¿Puedes leer adecuadamente los ejemplos anteriores? Te ayudo con el primero: tres elevado a la cinco. Tú continúa)
Sabiendo finalmente lo que es una potencia, pasaremos ahora a hablar de sus propiedades
1.- Exponente cero: Todo factor elevado a la cero es igual a uno.
¿Qué quiere decir esta propiedad? Que no importa lo que haya en la base, si el exponente es cero, el resultado de la operación es uno, SIEMPRE. Por ejemplo:
We see how the number, letter or large object is called 'BASE', and the number, letter or little thing (because yes, anything can also go there), is called 'EXPONENT'.
Having this new knowledge, we can state in a more formal way what a power is:
It is a mathematical operation where a factor called “BASE” is multiplied by itself as many times as indicated by another factor called “EXPONENT”, and is read as “a RAISED TO n”.
(Can you read the above examples properly? I'll help you with the first one: three to the fifth. You continue)
Finally knowing what a power is, we will now talk about its properties
1.- Zero exponent: Every factor raised to zero is equal to one.
What does this property mean? That no matter what is in the base, if the exponent is zero, the result of the operation is one, ALWAYS. For example:
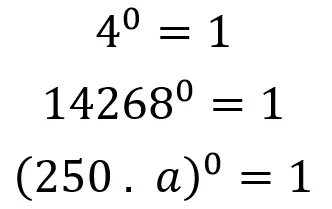

¿Cuatro a la cero? UNO, ¿catorce mil doscientos sesenta y ocho a la cero? UNO, ¿doscientos cincuenta por a elevado a la cero? UNO, ¿el Capitán América elevado a la cero? UNO. ¿Se entiende el punto?
2.- Multiplicación de potencias de igual base: se coloca la misma base y se suman los exponentes.
Sencilla de entender, así que pasemos a los ejemplos
Four to zero? ONE, fourteen thousand two hundred sixty-eight to zero? ONE, two hundred and fifty times a to zero? ONE, Captain America raised to zero? ONE. Is the point understood?
2.- Multiplication of powers of equal base: the same base is placed and the exponents are added.
Simple to understand, so let's move on to the examples
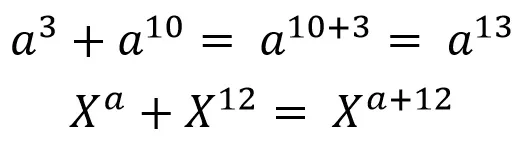
De esta propiedad aprendemos otra cosa importante: AQUELLO QUE NO SE PUEDA SUMAR (aplica para la resta, multiplicación y división) SE DEJA SIMPLEMENTE INDICADO, tal y como lo vemos en el segundo ejemplo. Como es imposible sumar “a” más 12, se deja indicada la operación.
3.- División de potencias de igual base: se coloca la misma base y se restan los exponentes.
Vamos directo a los ejemplos
From this property we learn another important thing: WHAT CANNOT BE ADDED (applies to subtraction, multiplication and division) IS SIMPLY LEFT INDICATED, as we see in the second example. Since it is impossible to add “a” plus 12, the operation is indicated.
3.- Division of powers of equal base: the same base is placed and the exponents are subtracted.
Let's go straight to the examples
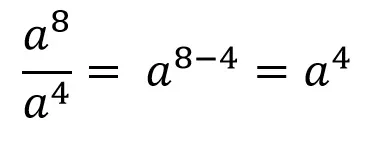

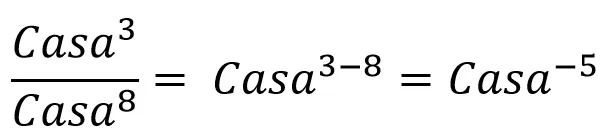
Del último ejemplo vemos dos cosas interesantes: la primera es que recordamos que tanto las bases como los exponentes pueden ser cualquier cosa, pero los principios matemáticos son los mismos; y la segunda es que los exponentes pueden quedar negativos (recuerden las propiedades de la resta: números con signos diferentes se restan y se coloca el signo del número mayor. En el ejemplo, el tres tiene un signo “+” que no se escribe, pero se sobreentiende).
Esa segunda parte, la de los exponentes negativos, nos lleva a la siguiente propiedad
4.- Una base con exponente negativo se convierte en una fracción cuyo numerador es UNO y el denominador es la potencia con el mismo exponente positivo.
Esto es más fácil de entender con un ejemplo. Veamos
From the last example we see two interesting things: the first is that we remember that both the bases and the exponents can be anything, but the mathematical principles are the same; And the second is that the exponents can be negative (remember the properties of subtraction: numbers with different signs are subtracted and the sign of the greater number is placed. In the example, three has a “+” sign that is not written, But it goes without saying).
That second part, that of the negative exponents, leads us to the next property
4.- A base with a negative exponent becomes a fraction whose numerator is ONE and the denominator is the power with the same positive exponent.
This is easier to understand with an example. Let's see
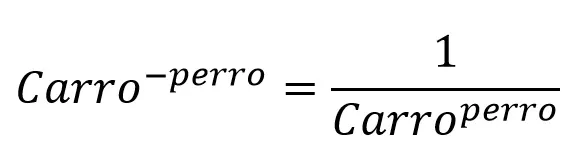
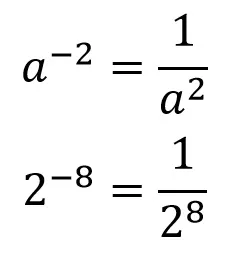
Nuevamente, no importa lo que haya en la base o el exponente, el principio matemático es el mismo. La única condición que se aplica EN LAS PROPIEDADES DE EXPONENTES NEGATIVOS es que la base NUNCA debe ser CERO.
La anterior propiedad nos conduce a la siguiente
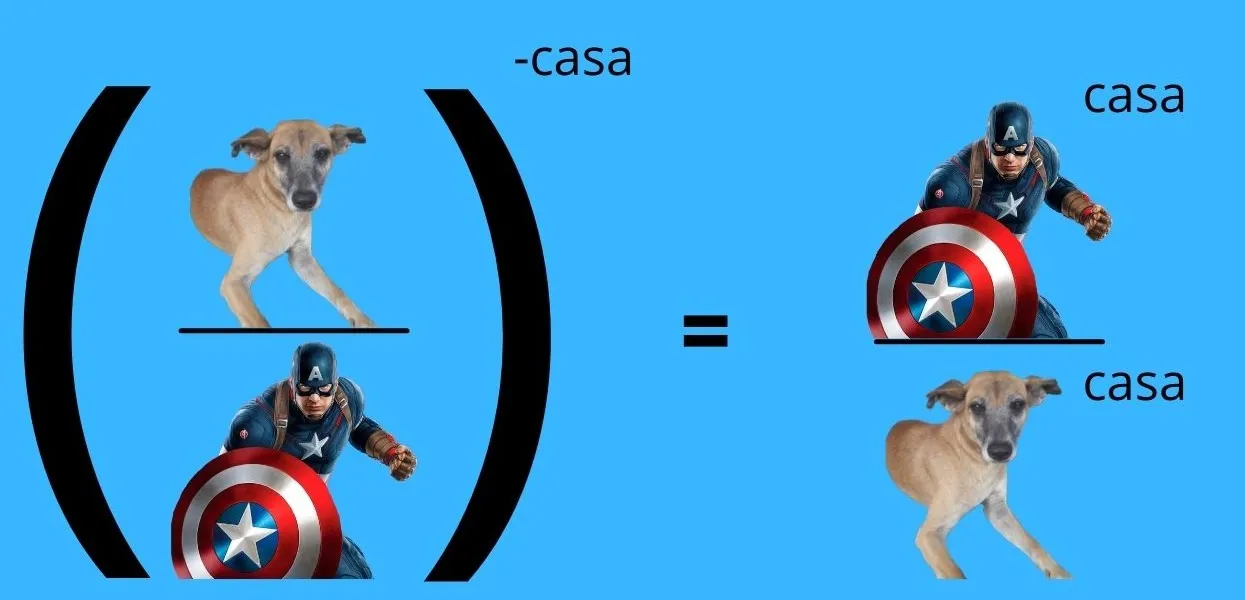
5.- Toda fracción elevada a un exponente negativo, se invierte y cada uno de sus términos se eleva a la misma potencia, pero positiva.
Esto es más fácil verlo que explicarlo, así que vamos con unos ejemplos:
Again, no matter what is in the base or the exponent, the mathematical principle is the same. The only condition that applies ON NEGATIVE EXPONENT PROPERTIES is that the base must NEVER be ZERO.
The previous property leads us to the next
5.- Every fraction raised to a negative exponent is inverted and each of its terms is raised to the same power, but positive.
This is easier to see than to explain, so let's go with some examples:
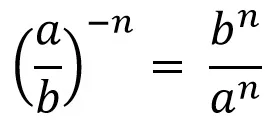
A partir de aquí, podemos pasar a la siguiente propiedad
6.- En toda fracción elevada a una sola potencia, ambos términos de la fracción quedan elevados al mismo exponente.
Esta propiedad vendría a ser la segunda parte de la propiedad anterior, y con un solo ejemplo bastará para entenderla
From here, we can move on to the next property
6.- In every fraction raised to a single power, both terms of the fraction are raised to the same exponent.
This property would be the second part of the previous property, and a single example will suffice to understand it.
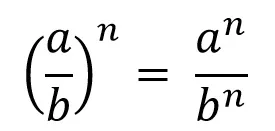
Y la última propiedad que necesitas conocer de las potencias es la siguiente
7.- Potencia de una potencia: se coloca la misma base y se multiplican los exponentes.
Como es bastante clara, veamos unos ejemplos
And the last property you need to know about the powers is the following
7.- Power of a power: the same base is placed and the exponents are multiplied.
As it is quite clear, let's see some examples
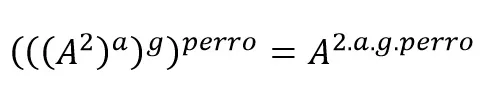
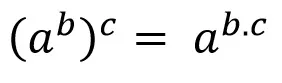
Y es así como llegamos al final de este post. Espero te haya sido de utilidad para entender mejor las potencias y sus propiedades. Si te gustó déjamelo saber con un like. Nos vemos en una próxima oportunidad, haaaaasta luego.
And this is how we come to the end of this post. I hope it has been useful for you to better understand the powers and their properties. If you liked it, let me know with a like. See you next time, seeeeeeeee you later.
