Hello everyone and welcome back to my blog.
Today I want to talk to you about the RSA public key cryptosystem, published in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman.
Introduction
The cryptosystem is a series of rules and procedures that two or more individuals decide to adopt to exchange messages privately.
Let's imagine that Alice wants to send a message to Bob and she only wants Bob to be able to read her message.
Alice wants to confess her love to Bob, but if her father Luigi finds out she gets in trouble!!
Alice will have to modify her message in some way, making it linguistically meaningless, explain to Bob how to derive the original message from the modified one, and finally send the modified message to her lover Bob.
The most trivial method that Alice can adopt is to convert the message into a number, directly associating the numbers to the letters of the alphabet.
For example in this way:
a = 1 , b = 2 , c = 3 , d = 4 , e = 5
f = 6 , g = 7 , h = 8 , i = 9 , j = 10
k = 11, l = 12, m = 13, n = 14, o = 15
p = 16, q = 17, r = 18, s = 19, t = 20
u = 21, v = 22, w = 23, x = 24, y = 25, z= 26
"Ciao" would become 3-9-1-15 so 39115
p.s. "Ciao" means "hello" in italian
By adopting only this criterion, after a while an attacker could figure out how to decode the message.
In fact, Luigi might notice that some digits appear more often than others and therefore associate these digits with the most common letters in our language, such as vowels and some consonants. After a few attempts Luigi will be able to read all of his daughter's secret messages.
Alice will then have to try a little more. In addition to converting the message into a number, she will also have to use some mathematical operation to transform it.
It's now that the RSA cryptosystem comes into play.
In the RSA cryptosystem each user has 2 keys, a public one used to encrypt messages and a private one used to decrypt messages.
We will denote Alice's keys with the pair (Ea, Da) while Bob's with (Eb, Db).
When Alice wants to send a message to Bob she takes Bob Eb's public key, she uses it to encrypt the message and sends it. Bob receives the encrypted message, takes his private Db key and decrypts it.
We'll now see in detail how everything happens, so as not to dwell too much in this part I will assume that you have a "modest" knowledge of algebra :)
Let's start by understanding how public and private keys are linked together and how to create them.
Public and Private key
You have to know that at the base of the RSA there is a very large composite number N, the product of 2 distinct secret prime numbers that we will call p and q, that is, N = pq
N is shared by all users and is used in both the encoding and decoding process of the message. It can be said that N is a kind of universal public key of the cryptosystem. In fact, for each composite number N there is an associated RSA cryptosystem which will be more or less secure on the basis of which N we have chosen.
Having said this, we assume that we have chosen two prime numbers p and q and that we have calculated N by multiplying p and q between them. Well at this point to create pairs of keys that are linked together by N, the RSA exploits the very important Euler-Fermat Theorem which states that:

where phi(N) is Euler's Phi Function which counts the number of numbers smaller than N that are coprime with N i.e. those that have no proper divisor (greater than 1) common to N.
Or in other words, Euler's Phi Function counts the number of numbers smaller than N that have the greatest common divisor equal to 1 with N. And a is an integer also coprime with N.
This theorem states that if we know the value of the function phi for a certain N and take any number a coprime with N, then if we calculate a raised to phi(N) we get a number that will have the remainder 1 with N.
Example:
N = 33 so phi(N) = 20
indeed: 1,2,4,5,7,8,10,13,14,16,17,19,20,23,25,26,28,29,31,32 are coprime with 33)
Let's choose a = 2 coprime with 33
calculate 2^20 = 1048576
now 1048576 is not divisible with 33, (1048576/33 = 31775.030303)
but the reminder is 1 as Euler Fermat's Theorem states
indeed: 1048576 = 33x31775 + 1
In order to exploit this Theorem, the public and private keys E, D must satisfy this relation:

that is, they must be the multiplicative inverse of the other module phi(N), practically if we multiply E and D together, as before we get a number that has the remainder 1, but this time in the division with phi(N).
It is also important to know that E and D must be coprime with phi(N), otherwise they could not be the multiplicative inverse of the other.
Using the example above:
phi(N) = 20
Let's choose E = 13 coprime with 20
then it follow that D = 17
indeed: 13x17 = 221
and 221 = 20x10 + 1
that is 221 has reminder 1 with 20
So E = 13 and D = 17
Now that we have the E and D keys, let's see how they are used to encode and decode messages.
Encoding
In the RSA the coding process is quite simple, take the message (number) a and raise it to E (public key) then take the reminder with N.
Let's call the encrypted message c.
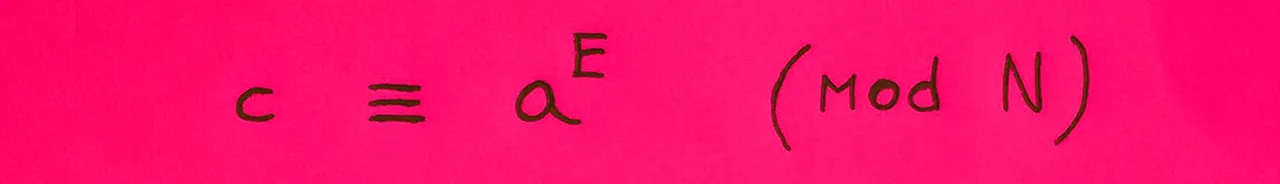
Example:
N = 33
Public key E = 13
Let's choose a number a coprime with N. a will be the message
a = 2
Calculate c
c = 2^13 mod 33 = 8
indeed 2^13 = 8192
and 8192 = 33x248 + 8
so the encrypted message is c = 8
Decoding
The decoding procedure is identical to the encryption one, but the D key is used.
You take the encrypted message c, raise it to D and take the reminder with N, you get the original message a.

Example:
N = 33
Private key D = 17
Encrypted message c = 8
Calculate c^D mod N
8^17 mod 33 = 2
indeed 8^17 = 2251799813685248
and 2251799813685248 = 33 x 68236357990462 + 2
so the reminder is 2 ,we then got the original message.
This magic is possible thanks to Euler Fermat's Theorem which intervenes in the decoding when the encrypted message c is raised to D and also thanks to the choice made on E and D.
Indeed E and D satisfy the relation

then it must exists an integer number t such that:
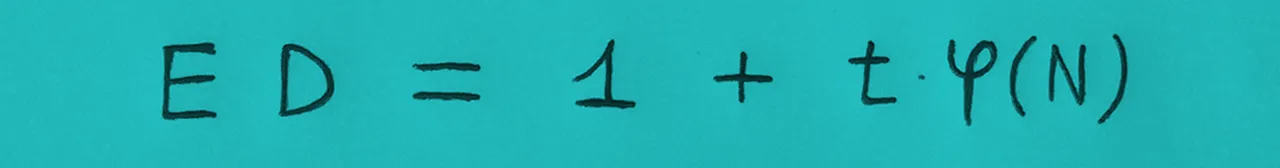
therefore since c is congruent to a^E module N, when in decoding it is raised to D we practically raise the original message a to ED in fact (aE)D = a^(ED)
Then using the relation that binds E to D and exploiting the theorem we obtain:

So we are able to decode the message with this simple procedure.
RSA hand made
Now let's see how to put into practice the notions seen above and create an RSA cryptosystem to encrypt the message in clear text: ciao.
As previously done we associate the word ciao with the number 39115. So a = 39115
Now we have to choose two prime numbers p and q to calculate N. I remind you that N must be coprime with a, so p and q must be too.
We choose p = 12149 and q = 19819 both prime and coprime with a.
To be sure that p and q are coprime with a just take two prime numbers greater than a.
Our N will be:
N = 12149 x 19819 = 240781031
At this point we need to create a pair of encryption and decryption keys. However, it is first necessary to calculate the value of Euler's Phi function for N.
In the case like this where N is the product of two distinct primes p and q, we can calculate the phi using the formula:
phi(N) = (p-1)(q-1)
Hence phi(240781031) = (12149-1)(19819-1) = 240749064
At this point we are able to create the keys, we must choose one and obtain the other.
We choose E = 1234567 as the public key to encrypt.
E is coprime with phi(N) so it admits multiplicative inverse. Its inverse will be our decryption private key D.
In the next few posts I will show you how to quickly calculate these multiplicative inverses using the Extended Euclidean Algorithm. For now, I'll just give you the results.
In this case we get D = 95886055
We can verify that 1234567 x 95886055 = 118377759263185
and 118377759263185 = 240749064 x 491706 + 1
The cryptosystem is ready, we can encode our message.
The encrypted message will be c = a^E mod N
c = 39115^1234567 mod 240781031
Also here to calculate this huge number I will show you in the next posts how to quickly calculate it using a certain algorithm.
Trust me for now ;)
We obtain c = 7709857
Now if we want to decode the message we take D and calculate c^D mod N then:
7709857^95886055 mod 240781031
trust me you get 39115 our clear message corresponding to ciao
Conclusions
Surely one of the strengths of the RSA lies in the speed with which the messages are encrypted and decrypted, as it is a question of making an exponentiation and then calculating a remainder.
These operations can be done very quickly using the above algorithm, even if the numbers are huge.
The safety of RSA lies in the still open problem of factoring numbers. In fact, there is still no algorithm that is able to factor a number quickly, that is, with a number of attempts that is at most a polynomial function of the number of digits of the input.
It is in fact essential that our number N is HUGE and therefore requires a lot of time to be factored by modern computers.
In fact, if we were able to factor N by finding p and q then we would also be able to calculate phi(N), and therefore we could get all the private keys of the users!! In fact it would be enough to take the public key of our victim and calculate its inverse multiplicative module phi(N)!!
Among the drawbacks, however, is the fact that it is not easy to find two very large prime numbers p and q.
However, there are rapid algorithms that allow us to distinguish composite numbers from prime ones.
And finally, the flaw I noticed is that you don't have the total freedom to choose the private or public key.
In fact, the key chosen must be a coprime number with phi(N), which sometimes narrows the range of possible choices a lot. In fact phi(N) being the product of two even numbers p-1 and q-1, could have many factors and therefore the coprime numbers with it will be few.
In these cases it is better to change p and q.
I close by telling you that I have implemented the RSA on discoBOT to encode the @discovery-it posting key. Now when I start discoBOT I have to enter a password I created (private key) which is used to decrypt the posting-key that I keep encrypted in a file.
I had a lot of fun implementing this cryptosystem and I am finally satisfied to have put into practice the things I learned at university!!
I hope I haven't bored you!! Hello everyone and see you soon!!

ITA
Ciao a tutti e bentornati nel mio blog.
Oggi voglio parlarvi del crittosistema a chiave pubblica RSA, pubblicato nel 1977 da Ron Rivest, Adi Shamir e Leonard Adleman.
Introduzione
Il crittosistema è una serie di regole e procedure che due o più individui decidono di adottare per scambiarsi dei messaggi in maniera privata.
Immaginiamo che Alice voglia mandare un messaggio a Bob e vuole che solamente Bob possa leggere il suo messaggio.
Alice vuole confessare il suo amore a Bob, ma se suo padre Luigi lo viene a sapere sono cazzi!!
Alice dovrà modificare in qualche modo il suo messaggio, rendendolo privo di senso dal punto di vista linguistico, spiegare a Bob come ricavare il messaggio originale da quello modificato e infine spedire il messaggio modificato al suo amante Bob.
Il metodo più banale che Alice può adottare è quello di convertire il messaggio in un numero, associando direttamente i numeri alle lettere dell'alfabeto.
Ad esempio in questo modo:
a = 1 , b = 2 , c = 3 , d = 4 , e = 5
f = 6 , g = 7 , h = 8 , i = 9 , j = 10
k = 11, l = 12, m = 13, n = 14, o = 15
p = 16, q = 17, r = 18, s = 19, t = 20
u = 21, v = 22, w = 23, x = 24, y = 25, z= 26
"Ciao" diventerebbe 3-9-1-15 quindi 39115
Ma adottando solo questo criterio, dopo un pò di tempo un attaccante potrebbe capire come decodificare il messaggio.
Luigi infatti potrebbe notare che alcune cifre compaiono più spesso di altre e quindi associare queste cifre alle lettere più ricorrenti nel nostro linguaggio, come ad esempio le vocali e alcune consonanti. Dopo qualche tentativo Luigi sarà in grado di leggere tutti i messaggi segreti di sua figlia.
Alice dovrà allora ingegnarsi un pò di più. Oltre a convertire il messaggio in numero, dovrà anche usare qualche operazione matematica per trasformarlo.
Ed è qui che entra in gioco il crittosistema RSA.
Nel crittosistema RSA ogni utente è in possesso di 2 chiavi, una pubblica usata per cifrare i messaggi e una privata usata per decifrare i messaggi.
Indicheremo le chiavi di Alice con la coppia (Ea , Da) mentre quelle di Bob con (Eb , Db).
Quando Alice vuole mandare un messaggio a Bob prende la chiave pubblica di Bob Eb, la usa per cifrare il messaggio e lo invia. Bob riceve il messaggio cifrato prende la sua chiave privata Db e lo decifra.
Vedremo ora nel dettaglio come il tutto avviene, per non dilungarmi troppo in questa parte assumerò che abbiate una "modesta" conoscenza dell'algebra :)
Iniziamo col capire come sono legate tra di loro le chiavi pubbliche e private e come poterle creare.
Chiave Pubblica e Privata
Dovete sapere che alla base dell' RSA vi è un numero composto N molto grande, prodotto di 2 numeri primi distinti segreti che chiameremo p e q, cioè vale N = pq
N è condiviso da tutti gli utenti e viene utilizzato sia nel processo di codifica sia in quello di decodifica del messaggio. Si può dire che N è una sorta di chiave pubblica universale del crittosistema. Infatti per ogni numero composto N esiste un crittosistema RSA associato che sarà più o meno sicuro in base a quale N abbiamo scelto.
Detto questo assumiamo di aver scelto due numeri primi p e q e di aver calcolato N moltiplicando p e q tra di loro. Bene a questo punto per creare delle coppie di chiavi che siano legate tra di loro tramite N, l'RSA sfrutta l'importantissimo Teorema di Eulero-Fermat il quale afferma che:

dove phi(N) è la funzione phi di Eulero che conta il numero di numeri minori di N che sono coprimi con N cioè quelli che non hanno alcun divisore proprio (maggiore di 1) comune a N.
O detto in altri termini, la phi di Eulero conta il numero di numeri minori di N che hanno il massimo comun divisore uguale a 1 con N. Mentre a è un numero intero anch'esso coprimo con N.
Questo teorema afferma che se noi conosciamo il valore della funzione phi per un certo N e prendiamo un qualsiasi numero a coprimo con N, allora se calcoliamo a elevato alla phi(N) otteniamo un numero che avrà resto 1 nella divisione con N.
Esempio:
N = 33 dunque phi(N) = 20
infatti: 1,2,4,5,7,8,10,13,14,16,17,19,20,23,25,26,28,29,31,32 sono coprimi con 33)
scelgo a = 2 coprimo con 33
calcolo 2^20 = 1048576
ora 1048576 non è divisibile per 33, (1048576/33 = 31775.030303)
ma il resto è 1 come afferma il Teorema di Eulero Fermat
infatti: 1048576 = 33x31775 + 1
Per poter sfruttare questo Teorema le chiavi pubbliche e private E, D devono soddisfare questa relazione:

devono cioè essere una l'inverso moltiplicativo dell'altra modulo phi(N), praticamente se moltiplichiamo tra loro E e D otteniamo come prima un numero che ha resto 1, ma questa volta nella divisione con phi(N).
Inoltre è importante sapere che E e D devono essere coprime con phi(N), altrimenti non potrebbero essere una l'inverso moltiplicativo dell'altra.
Usando l'esempio di prima:
phi(N) = 20
scelgo E = 13 coprimo con 20
allora trovo che D = 17
infatti: 13x17 = 221
e 221 = 20x10 + 1
cioè 221 ha resto 1 con 20
Dunque E = 13 e D = 17
Ora che siamo in possesso delle chiavi E e D, vediamo come vengono usate per codificare e decodificare i messaggi.
Codifica
Nell'RSA il processo di codifica è piuttosto semplice, si prende il messaggio (numero) a e lo si eleva alla E (chiave pubblica) poi se ne prende il resto con N.
Chiamiamo c il messaggio cifrato.
Sarà:
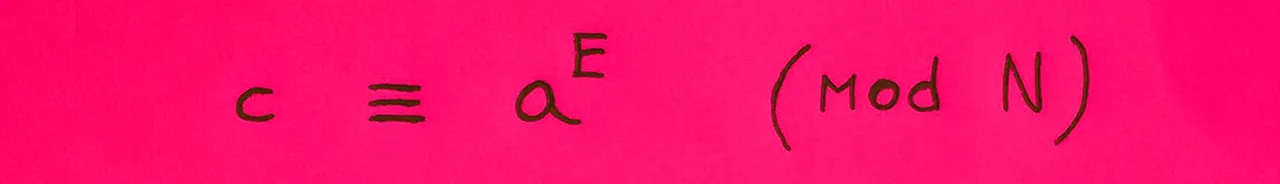
Esempio:
N = 33
Chiave pubblica E = 13
Scelgo un numero a coprimo con N. a sarà il messaggio
a = 2
Calcolo c
c = 2^13 mod 33 = 8
infatti 2^13 = 8192
e 8192 = 33x248 + 8
dunque in messaggio cifrato è c = 8
Decodifica
La procedura di decodifica è identica a quella di codifica, ma si usa la chiave D.
Si prende il messaggio cifrato c, lo si eleva alla D e se ne prende il resto con N, si ottiene a il messaggio originale.

Esempio:
N = 33
Chiave privata D = 17
Messaggio cifrato c = 8
Calcolo c^D mod N
8^17 mod 33 = 2
infatti 8^17 = 2251799813685248
e 2251799813685248 = 33 x 68236357990462 + 2
dunque il resto è 2 e abbiamo quindi ottenuto il messaggio originale.
Questa magia è possibile grazie al Teorema di Eulero Fermat che interviene nella decodifica quando si eleva alla D il messaggio cifrato c e anche grazie alla scelta fatta su E e D.
Infatti E e D soddisfano la relazione

dunque esiste un numero intero t tale che:
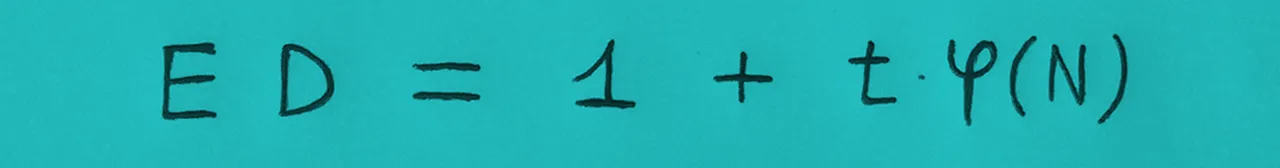
quindi essendo c congruo a a^E modulo N, quando nella decodifica lo si eleva alla D praticamente eleviamo il messaggio originale a alla ED infatti (aE)D = a^(ED)
Allora usando la relazione che lega E a D e sfruttando il teorema si ottiene:

Quindi siamo in grado di decodificare il messaggio con questa semplice procedura.
RSA fatto a mano
Vediamo ora come mettere in pratica le nozioni viste sopra e creare un crittosistema RSA per cifrare il messaggio in chiaro: ciao.
Come fatto in precedenza associamo alla parola ciao il numero 39115. Quindi a = 39115
Ora dobbiamo scegliere due numeri primi p e q per calcolare N. Ricordo che N deve essere coprimo con a, quindi anche p e q lo devono essere.
Scegliamo p = 12149 e q = 19819 entrambi primi e coprimi con a.
Per essere sicuri che p e q siano coprimi con a basta prendere due numeri primi maggiori di a.
Il nostro N sarà:
N = 12149 x 19819 = 240781031
A questo punto dobbiamo creare una coppia di chiavi di cifratura e decifratura. Però è necessario prima calcolare il valore della phi di Eulero per N.
Nel caso come questo in cui N è il prodotto di due numeri primi distinti p e q, possiamo calcolare la phi utilizzando la formula:
phi(N) = (p-1)(q-1)
Dunque phi(240781031) = (12149-1)(19819-1) = 240749064
A questo punto siamo in grado di creare le chiavi, dobbiamo sceglierne una e ricavare l'altra.
Scegliamo E = 1234567 come chiave pubblica per cifrare.
E è coprimo con phi(N) quindi ammette inverso moltiplicativo. Il suo inverso sarà la nostra chiave privata di decodifica D.
Nei prossimi post vi mostrerò come calcolare rapidamente questi inversi moltiplicativi usando l'Algoritmo Euclideo Esteso. Per adesso mi limito a darvi i risultati.
In questo caso si ottiene D = 95886055
Possiamo verificare che 1234567 x 95886055 = 118377759263185
e 118377759263185 = 240749064 x 491706 + 1
Il crittosistema è pronto, possiamo codificare il nostro messaggio.
Il messaggio cifrato sarà c = a^E mod N
c = 39115^1234567 mod 240781031
Anche qui per calcolare questo enorme numero vi mostrerò nei prossimi post come calcolarlo rapidamente usando un certo algoritmo.
Per adesso fidatevi di me ;)
Si ottiene c = 7709857
Adesso se vogliamo decodificare il messaggio prendiamo D e calcoliamo c^D mod N quindi:
7709857^95886055 mod 240781031
fidatevi si ottiene 39115 il nostro messaggio in chiaro corrispondente a ciao
Conclusioni
Sicuramente uno dei pregi dell'RSA sta nella rapidità con cui i messaggi vengono cifrati e decifrati, in quanto si tratta di fare un elevamento a potenza e poi di calcolare un resto.
Queste operazioni possono essere eseguite molto rapidamente usando l'algoritmo sopra citato, anche se i numeri sono enormi.
La sicurezza dell'RSA sta nel problema ancora aperto della fattorizzazione dei numeri. Infatti non esiste ancora un algoritmo che sia in grado di fattorizzare un numero rapidamente, cioè con un numero di tentativi che è al più funzione polinomiale del numero di cifre dell'input.
E' infatti fondamentale che il nostro numero N sia ENORME e che quindi richieda moltissimo tempo per essere fattorizzato dai moderni calcolatori.
Se infatti fossimo in grado di fattorizzare N trovando p e q allora saremmo anche in grado di calcolare phi(N), e quindi potremmo ottenere tutte le chiavi private degli utenti!! Infatti basterebbe prendere la chiave pubblica della nostra vittima e calcolare il suo inverso moltiplicativo modulo phi(N)!!
Tra i difetti invece vi è il fatto che non è facile trovare due numeri primi p e q molto grandi.
Esistono però algoritmi rapidi che ci permettono di distinguere i numeri composti da quelli primi.
E infine il difetto che ho notato io è che non si ha la totale libertà di scegliere la chiave privata o pubblica.
Infatti la chiave scelta dovrà essere un numero coprimo con phi(N), il che a volte restringe molto il campo delle scelte possibili. Infatti phi(N) essendo il prodotto di due numeri pari p-1 e q-1, potrebbe avere molti fattori e quindi i numeri coprimi con essa saranno pochi.
In questi casi conviene cambiare p e q.
Chiudo dicendovi che ho implementato l'RSA su discoBOT per codificare la posting key di @discovery-it. Ora quando avvio discoBOT devo immettere una password da me creata (chiave privata) la quale viene usata per decodificare la posting-key che conservo cifrata in un file.
Mi sono divertito molto ad implementare questo crittosistema e sono finalmente soddisfatto di aver messo in pratica le cose imparate all'università!!
Spero di non avervi annoiato!! Ciao a tutti e a presto!!
Vote for Us as Witness!
Join our community!


