Este miércoles pasado estuve presente en una pequeña reunión familiar y a un tío se le ocurrió plantear acertijos matemáticos para levantar el ánimo en la fiesta, y se me quedó grabado en mi memoria la pregunta: ¿cuánto vale 11 más 3?, la mayoría respondió 14, pero Él salió con que la respuesta correcta era "2".

Pensé, tal vez se trata de un truco algebraico, pero inmediatamente dibujó un círculo y colocó la numeración del 1 al 12, como la de un reloj, señaló el número 11 y se desplazó 3 unidades en el sentido de las agujas del reloj y resultó detenerse sobre el número 2. A partir de ese momento aprendí que el sistema de aritmética modular puede convertirse en una potente herramienta para desarrollar la Matemática más divertida.

Sistema de Aritmética Modular:

para explicarlo de la manera más sencilla posible, este tipo de relación matemática se emparenta con la operación de división y el teorema del resto, donde dividimos un elemento numérico "N" (numerador) entre un número "D" (denominador), resultando en un valor "Q" (resultado de la división) más una cantidad denominada "R" (residuo).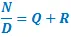

Esta relación se reescribe en términos de la aritmética modular como:

Siguiendo el ejemplo del acertijo matemático, el numerador estaría dado por la suma 11 + 3, el denominador sería en base a 12 divisiones del círculo, así:

N = (11+3) = 14
D = 12



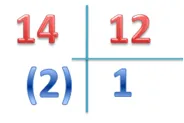
(14) mod12 = R
R = 2

tal como lo planteó mi tío.

Círculo Modular:

resulta en representar el número modular desde 0 hasta un dígito menor indicado por el módulo: 0 1 2 3 4 5 6 7 8 9 10 11 con un total de 12 dígitos y se continúa siguiendo esta numeración.

Aritmética modular para la multiplicación

Como esta publicación la realizo con el fin de mostrar que no hay trucos ni secretos en una representación del sistema aritmético modular, representaré una tabla numérica de resultados al determinar la multiplicación de 2 números enteros con módulo 5, veamos el siguiente ejemplo:

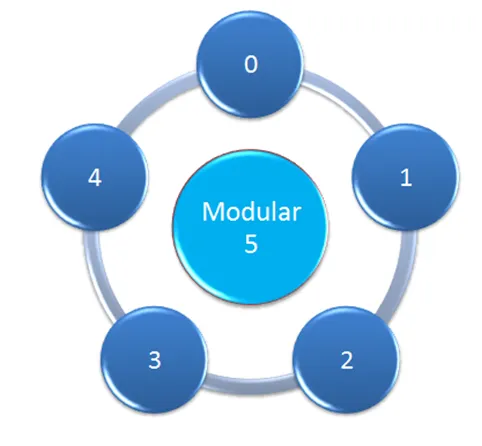
Como el módulo que seleccioné es mod = 5, la numeración consecutiva en el sistema aritmético modular se representa así:

0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, ..........

---

podemos determinar el resultado de (4*2) mod5, resolviendo (4*2) = 8, así que podemos reescribir 8 mod5 = ?

Como lo mencioné anteriormente, debemos considerar el residuo del cociente de 2 números:

8 mod5 = 3

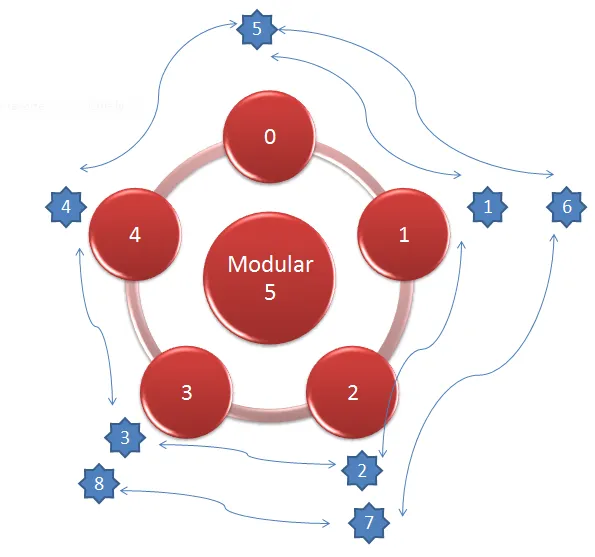
Nada de secretos, sólo debemos tomar en cuenta el contexto de las operaciones aritméticas sobre la base del sistema aritmético modular que estemos trabajando y nos ajustamos a la numeración coordinada por el módulo y repetición de valores numéricos.

Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de Alexas_Fotos: Portada de Aritmética modular
• Blog: Suma y resta modular
• Wikipedia: Sistema aritmético modular

Las funciones matemáticas son expresiones que relacionan
las variables de una igualdad o desigualdad,
para hallar la solución de la ecuación o inecuación