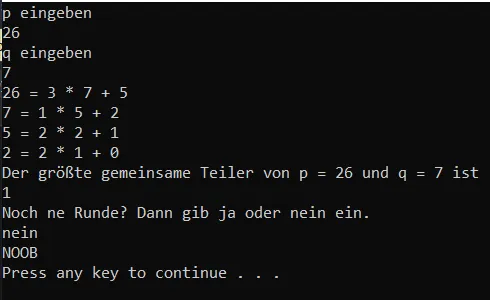
Während ich an meinen Post zum Thema Kryptographie saß und den euklidischen Algorithmus so in meine Tastatur kloppte, habe ich mir gedacht, dass man das ja auch mit Python machen könnte.
Als ultimative Python-Laie und auch Programmierlaie war dies zwar leichter gedacht als getan, aber mit der Hilfe von @altonos und @fehlerbeheber konnte ich die meisten meiner Noob-Fragen klären.
Mein Quest war die Berechnung des größten gemeinsamen Teilers mithilfe des euklidischen Algorithmus. Natürlich wollte ich mir kein fertiges "Produkt" schnappen, sondern mir selbst überlegen wie ich dies umsetzen könnte. Mein fertiges "Produkt" macht was es soll. Und das ist ja schon mal ein Erfolg.
Anschließend habe ich mir andere Versionen mal angeguckt. Diese sind deutlich kürzer. Dennoch gilt:
Der Weg ist das Ziel
Ich habe erstmal ein bis zwei Tutorials überflogen. Man muss ja auch die Syntax kennen (Schleifen, Funktionen etc.). Ergänzend sei erwähnt, dass ich minimale Erfahrung mit mathematischer Programmierung habe, welche ich hin und wieder mal mit C++ oder Matlab gemacht habe. Letztes Jahr hatte ich mir auch mal Python und Beem installiert und sogar einen Block ausgelesen (mithilfe von @felixxx). (Anm. d. Noobs: Ich weiß voll krass.)
Nach den oberflächlich gewatchten Tutorials habe ich dann auch gleich losgelegt. Als erstes habe ich grob über einen Pseudocode nachgedacht. Meine Idee war das ganze über einen Schleife in einer Schleife zu lösen. Das hat nicht immer so funktioniert wie es soll. Damit die Schleife auch das macht was sie soll, mussten die Variablen richtig umbenannt werden. 10 Versuche später hat mir dann @fehlerbeheber auf die Sprünge geholfen und was soll ich sagen - es ging. Naja zumindest fast.
Beim nächsten Problem habe ich dann @altonos gefragt. Der war allerdings durch zocken abgelenkt und ich brütete weiter. Als ich dann damit fertig war, machte die Schleife nicht genau was sie machen sollte. Drei Kaffee später haben ich dann auch das gelöst - etwas geschummelt, aber was solls 😅.
Zusätzlich wollte ich die Zwischenschritte in Listen speichern, da ich eigentlich nicht den euklidischen Algorithmus brauche, sondern den erweiterten euklidischen Algorithmus. Als dies dann endlich funktioniert hat, war die letzte Iteration allerdings falsch. Diese habe ich dann einfach aus der Liste gelöscht. Außerdem haben nicht alle Fälle funktioniert. Zum Beispiel falls die eine Zahl ein Vielfaches der anderen ist, ging nix mehr. Durch das Brüten über die anderen Probleme, hat sich dieses Problem wie von Geisterhand selbst gelöst.
Gegen Ende kam ich dann auch noch auf die Idee die Rechnung selbst visuell darzustellen. Da aber die letzte Iteration fehlte (was für den erweiterten euklidischen Algorithmus irrelevant wäre), habe ich diese dann noch dazu geschummelt.
Während der Finalisierungsphase bekam ich dann noch ein paar Tricks von @altonos und es läuft wie eine Bee. Ich habe zwar etwas geschummelt und dabei etwas gelitten, aber selbstgemacht ist doch noch am schönsten.
Hier ist meine epischer Erguss:
Python
def ggT(p,q):
v_k=[]
a=p
b=q
if q>p:
a=q
b=p
v_a=[a]
v_b=[b]
while a>b:
k=0
while a>b:
a=a-b
k=k+1
c=b
b=a
a=c
v_k.append(k)
v_a.append(a)
v_b.append(b)
v_a.pop(-1)
v_b.pop(-1)
v_k.pop(-1)
for i in range(len(v_k)):
print(v_a[i],'=',v_k[i],'*',v_b[i],'+',v_b[i+1])
print(v_a[-1],'=',v_a[-1]//v_b[-1],'*',v_b[-1],'+','0')
print('Der größte gemeinsame Teiler von', 'p', '=', p, 'und', 'q', '=', q , 'ist')
return v_b[-1]
print('p eingeben')
p=int(input())
print('q eingeben')
q=int(input())
print(ggT(p,q))
while True:
print('Noch ne Runde? Dann gib ja oder nein ein.')
l=input()
if l=='ja':
print('p eingeben')
p=int(input())
print('q eingeben')
q=int(input())
print(ggT(p,q))
if l=='nein':
print('NOOB')
break
else:
break
Und noch ein weiterer Output:
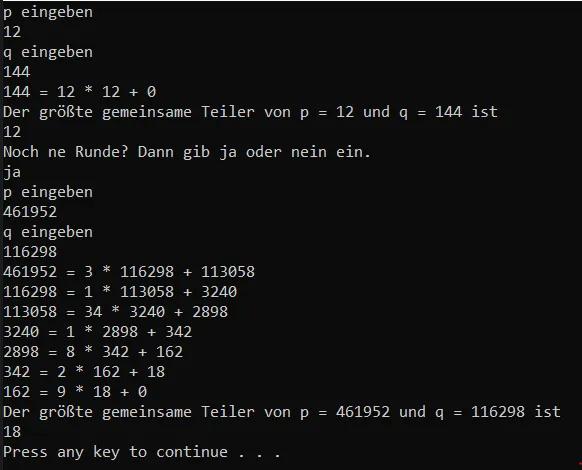
Wir lesen uns, wenn ich mit dem erweiterten euklidischen Algorithmus fertig bin.
