
Image contains: https://en.wikiversity.org/wiki/RLC_circuit
Introduction
Hello it'a me again @drifter1! Today we continue with the Electromagnetism series to talk about the Resonance of Parallel R-L-C circuits. To not get lost you should read the previous articles about such circuits in the Mutual and Self Induction chapter, but also the previous articles of the current chapter! So without further do, let's get started!
Parallel R-L-C circuit
RLC Circuits consist of three components: Resistance R, Inductance L and Capacitance C. Last time we talked about the series connection of those three elements that build a so called Series or Voltage Resonance RLC circuit. Another way of connecting those three components/elements together is in parallel. When connecting in parallel the components have the same voltage, but different currents. This means that part of the current is flowing through the resistor (R), part of it in the inductor (L) and the rest on the capacitor (C). The current flowing through each of those components or branches can be different to each other, but the total vector sum of all of them together of course has to give us the supply current Is. For this sum we of course have to use Kirchhoff's current law (KCL) All these can be summarized in the following two equations:
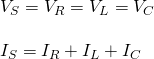
The sum of course is a "vector" sum and not an algebraic sum.
The same way as with series circuits we can solve this circuit using phasor vectors, but also using Kirchhoff's laws and Mathematical Analysis. What changes now is the current and so the three current vectors now have to be plotted in respect to the (supply) voltage. The current and voltage in resistors are in-phase and so the current flowing through the resistor is being noted parallel to the x-axis. The current in capacitors leads over the voltage by a 90 degree phase difference, whilst the current in inductors "lags" behind by 90 degrees. Doing all this we end up with a so called Current Triangle (similar to the Voltage Triangle of series circuits). The difference in magnitude between the current in the capacitor and inductor will make the circuit either capacitive or inductive. Here a graph so that you can understand it better:
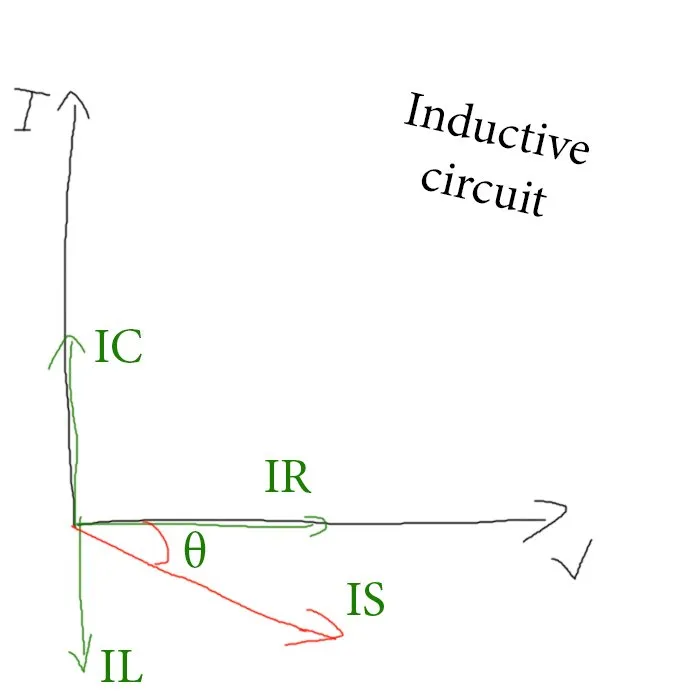 Based on the graph at:https://www.electronics-tutorials.ws/accircuits/parallel-circuit.html
Based on the graph at:https://www.electronics-tutorials.ws/accircuits/parallel-circuit.html
The Inductive component is mostly "stronger" then the capacitive one and so most circuits are inductive. This means that the previous diagram applies on most cases. Using the Pythagora's theorem we can determine the total current Is as:

The other way would be using Kirchoff's Current Law (KCL). Since the voltage across the circuit is common we can use KCL at any junction to find the total current. Solving a differential equation we will get the same equation that we calculated through the vector or phasor method...
The Impedance of such circuits has not been analyzed yet in any previous article, so let's get into it now! Parallel RLC circuits produce complex impedance's for each parallel branch. As the equation is somewhat "opposite" and complex we use the reciprocal of impedance that we call Admittance and is much more convenient to use. The total admittance with symbol Y can be found as a addition of the parallel admittances of each parallel branch. The total Impedance afterwards is 1/Y. This all can be summarized as following:
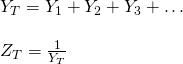
As a comparison the total impedance can also be calculated as:
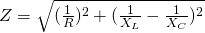
which can be used for a simple RLC circuit that contains only one of the three components on each branch, which means that one branch is "resistive", one "inductive" and one "capacitive".
Admittance defines the ease at which a circuit composed of resistances and reactances allows current to flow when a voltage is being applied, by also taking into account the phase difference between them. In the same notion we can also define the Conductance of resistance as G (1/R) and Suspectance of pure reactance (X). We of course have Inductive and Capacitive Suspectance. Combining all these together we get the so called Admittance triangle :
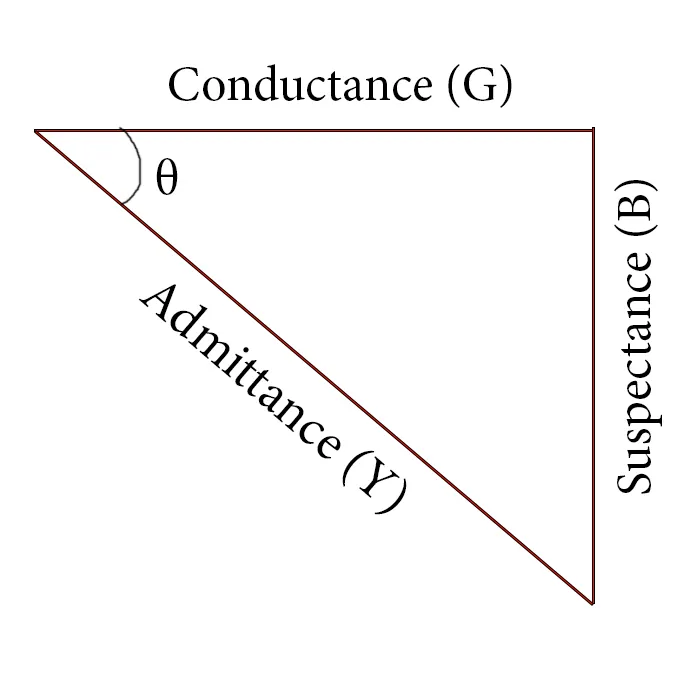 Based on the graph at:https://www.electronics-tutorials.ws/accircuits/parallel-circuit.html
Based on the graph at:https://www.electronics-tutorials.ws/accircuits/parallel-circuit.html
By using the Pythagora's theorem again we can find the same equation as before, something that shows us that the equation is somewhat "universal":

With Z = 1/Y we then get the same equation! :)
Lastly let's now also get into the power factor of such parallel RLC circuits. As the Admittance Y is a complex or vector quantity we can also write it down as Y = G - iB (in series circuits the impedance was Z = R + iX).Therefore using the polar form the power factor angle θ is given by:
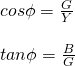
So, to summarize everything again in parallel circuits we talk about:
- current instead of voltage
- conductance instead of resistance
- suspectance instead of reactance
- admittance instead of impedance
Parallel Resonance
After all this entry information we can now finally get into the actual topic of today's post. In parallel RLC circuits we talk about a Parallel resonance, also called anti-resonance that occurs when the current and supply voltage are in-phase. At resonance there is a large circulating current between the inductor and capacitor due to the energy of the oscillations, therefore we also say that parallel circuits produce a so called current resonance. The energy of a parallel resonant circuit is being stored inside of the magnetic field of the inductor and the electric field of the capacitor. This energy is being constantly transferred back and forth between those two components resulting in zero current and energy draw from the supply. The instantaneous currents along each of those components are equal and opposite and therefore cancel each other out. The total current flowing through the circuit is equal to the vector sum of all these currents, which means that the total current is equal to the current flowing through the resistor (Is = IR).Resonance Frequency
At resonance the reactances or suspectances of the inductor and capacitor are of course equal to each other. The voltages are of course equal and opposite (VL = -VC). Applying KVL we therefore and end up with: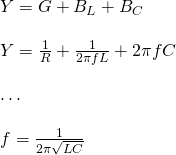
Oh! It's the same equation as with series resonance circuits!
We end up with the same equation as in the previous article about series rlc circuits, which means that it makes no difference if we connect the inductor or capacitor in series or parallel.
Parallel RLC circuit at Resonance
Let's now get into more in-depth stuff about this resonance thingy. At resonance the LC part of the RLC circuit acts like an open circuit and so the current is being determined by the resistor R. The total impedance of a parallel resonance circuit is therefore equal to the resistance in the circuit (Z = R). More specifically, the impedance of the parallel circuit reaches it's maximum value that's equal to the resistance creating a circuit condition of high resistance and low current. Having no reactance/suspectance the total circuit current is of course in-phase with the supply voltage. Changing the resistance R of the circuit can change the frequency response of it. The value of R of course affects the amount of current that is flowing through the circuit, as both L and C remain constant.The maximum impedance that a circuit reaches at resonance is called dynamic impedance and can be graphed as following:
This graph/diagram is exactly opposite when compared to the serial one! The parallel circuit Impedance is at maximum at resonance, which means that the admittance must be at it's minimum. Unlike in series resonance circuits, the resistor in parallel resonance circuits has a damping effect on the circuits bandwidth making the circuit less selective. Since the current is constant for any value of Z the voltage across the parallel resonance cirucit has the same shape as the total impedance. This means that the voltage waveform across such circuits is generally taken across the capacitor. Also, at resonance, the admittance is not only at it's minimum but also equal to the conductance (1/R). This means that the suspectances of the inductor and capacitor are also equal (BL = BC) turning the total suspetance zero. The inductive susceptance is inversely proportional to the frequency, while the capacitive susceptance is directly proportional to the frequency. Combining those together gives us a total suspectance that as a function of frequency can be represented by a hyperbolic curve. The maximum dynamic impedance can be calculated by:
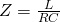
An equation that combines all three components!
Continuing on we could also talk about Bandwidth, Selectivity and Quality...that I will leave out, cause it's described perfectly at:
https://www.electronics-tutorials.ws/accircuits/parallel-resonance.html>
REFERENCES:
- https://www.electronics-tutorials.ws/accircuits/parallel-circuit.html
- https://www.electronics-tutorials.ws/accircuits/parallel-resonance.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/electric/parres.html
Mathematical equations that I had in this post where drawn using quicklatex!
Previous articles of the Electromagnetism series
Here we only have the previous two "chapters" and the current one....
Electromagnetic Induction:
Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law
Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization
Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields
Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)
Maxwell's equations -> What they are, each equation analyzed separately
Electromagnetic Induction exercises -> examples all around Electromagnetic Induction
Mutual and Self Induction:
Mutual Inductance -> Mutual Inductance, applications
Self Induction -> Self Induction, Lenz's law, Inductance of a Coil
Magnetic Energy Density -> Energy stored in a magnetic field (or inductor), Magnetic energy density, Coaxial Cable Inductance Example
R-L circuits -> R-L circuit energizing, de-energizing, Characteristic time constant
L-C circuits -> L-C circuit, oscillations, energy cases, applications
R-L-C circuits -> R-L-C circuit, oscillation, applications
Mutual and Self Induction exercises -> examples all around Mutual and Self Induction
Alternating current:
Getting into Alternating current -> Phasor diagrams, Alternating current, Average (RMS) current and voltage, Differences, Advantages/Disadvantages
Electric Reactance in AC circuits -> Resistors, Inductor and Capacitor Reactance in AC circuits
Series R-L-C circuits Impedance -> Series R-L-C circuits, Phasor Diagrams, Impedance
Power in AC circuits -> DC Resistive circuit, Power in AC circuits (resistive, reactive), Power Factor
Resonance in Series R-L-C circuits -> Series R-L-C circuit, Series Resonance
Final words | Next time
And this is actually it for today's post and I hope that you learned from it! Next time we will get into AC Transformers!


Keep on drifting!
