
Custom Thumbnail
Introduction
Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Exercises/Examples all around the Alternating current "chapter" we covered in the previous articles. By that I mean examples around Alternating Current Basics, Electric Reactance, Series R-L-C Impedance, AC Power, Series R-L-C and Parallel R-L-C circuit Resonance, AC Transformers. Lot's of these topic don't have "good" examples/applications, but I will still make a small theory recap about them. So, without further do, let's get started!
To stay organized each article/topic will be covered on it's own...as always!
Alternating current Basics
Let's start out with the first article/topic, which was an introduction to Alternating current (AC), giving a small recap. Let's first get into some theory and then into how we use/apply the formulas.
Alternating current follows sinusoidal waveforms that are periodically changing with time. An AC waveform is plotted similar to a sinφ trigonometric function and being represented mathematically as:
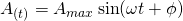
where:
- A is the value at specific time t in seconds
- Amax the maximum value that this quantity can reach (remmeber that sinφ and cosφ give values in the range [-1, 1])
- ω the angular velocity of the waveform
- φ the phase difference in comparison to a "regular" sinus-function
Two sinusoidal waveforms that describe current, voltage etc. can therefore be in-phase or out-of-phase. When out-of-phase we define the phase relationship as a lagging or leading phase difference in angle φ.
Being similar to a trigonometric sinus or cosinus function we can use a rotating vector or phasor to describe the values of a complete cycle or revolution of 2π (360 degrees). Rotating this vector anti-clockwise and including a phase difference of φ angle, we can describe the values through-out a whole period as following:

Image source: https://www.electronics-tutorials.ws/accircuits/phasors.html
Note that the length of the vector/phasor is equal to the signals Magnitude (or maximum value).
Instead of angular velocity ω, we mostly use the frequency f of the signal, for our calculations. That way the waveform equation turns into:

where ω = 2πf = 2π/T (T is the period).
Besides the theory, we also covered some very important mathematical equations/formulas. The instantaneous value of current and voltage doesn't mean much. What is of great importance is how "effective" a signal is. This can be measured easily by an "average" value of current/voltage that we call RMS (Root-Mean-Squared). The RMS value of Voltage and current for half a period is given as:
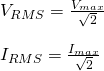
Let's get into a small application around all that...
Application
Consider an AC voltage supply of:
- 10V magnitude
- 5Hz frequency
- 90° phase angle
Calculate:
- The instantaneous voltage at t = 1 sec
- The instantaneous voltage at t = 1.44 sec
- The average/RMS voltage
1.
Using the equation of a sinusoidal waveform we get:
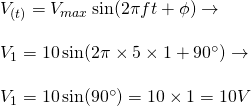
2.

3.
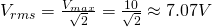
Electric Reactance
Resistance in AC circuits acts exactly the same way as in DC circuits, cause voltage and current are "in-phase" (o phase angle/difference) inside of resistors. "Plain" resistance doesn't depend on the frequency of the signal. Inductors and Capacitors on the other hand depend on the frequency of the signal. Inductive and Capacitive elements/components have a so called Reactance, which is a property that opposes the change in electric current or voltage. Capacitance, inductance and resistance are all inherent and natural properties of an element. Reactance of course makes only sense in AC circuits. To make everything simpler we of course consider ideal resistors that have zero reactance and ideal inductors/capacitors that consist entirely of reactance.
There are two types of reactance:
- capacitive reactance (Xc)
- inductive reactance (XL)
"Inductive" circuits, where inductive reactance is stronger then capacitive reactance (most AC circuits) have a total reactance of:

Let's get into each one more in-depth...
Capacitive reactance
Inside of capacitors current and voltage have a phase difference. More specifically the voltage "laggs" behind (or follows) the current by one-fourth of a cycle or by a 90° phase angle.
Therefore the voltage and current can be represented as:
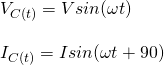
Thinking of this reactance as some form of resistance we can apply Ohm's law. Doing so we get that the current is given by:
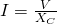
After analyzing a purely capacitive circuit using Kirchhoff's laws and Calculus we find that the capacitive reactance is given by:

This reactance is inversely proportional to the capacitance C of the Capacitor and frequency of the circuit.
Example:
Let's consider a capacitor of Capacitance C = 10F and an AC voltage supply of 10 V with frequency f = 5Hz and no phase-angle.
Find:
- the capacitive reactance of this capacitor
- the voltage and current at t = 1 sec.
1.
The capacitive reactance can be found easily using:
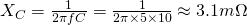
2.
Using the waveform equations for voltage and current we get:

Inductive reactance
Inside of inductors the voltage leads over the current by one-fourth of a cycle or 90 phase angle.Inductors oppose the change in current, which explains why the current "laggs" behind the voltage. Using all this we get the following mathematical represenation using sinusoidal waveforms:

Considering inductive reactance being an effective resitance Ohm's law gives us:
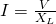
Again using Kirchhoff and Calculus we can find an mathematical expression that gives us the inductive reactance of a purely inductive circuit as:
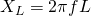
This shows us that inductive reactance is directly proportional to the frequency and inductance.
Example:
Let's now consider an inductor of inductance L = 2H and the same AC voltage supply as before.
Let's calculate:
- the inductive reactance of this inductor
- the voltage and current at t = 2 sec
1.
The inductive reactance can be found easily using:

2.
Using the waveform equations for voltage and current we get:
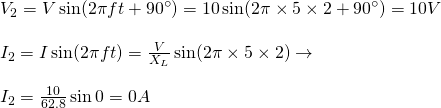
The values of time that I chose in those examples where so simple that we could calculate them even without calculating :P Of course voltage and current cannot be at the maximum magnitude at the same time. When one is max the other is zero (for 90 degrees phase angle)!
Series R-L-C circuits Impedance
The combination of both reactances (capacitive and inductive) and resistance gives us something that we call Impedance. In series R-L-C circuits, which are circuits that consist of resistance R, inductance L and capacitance C and have those components connected in serial, this combined effect of reactance and resistance can be analyzed very easily. Voltage and current have a linear relationship. In series circuits all components have the same current I, which means that:
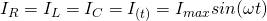
Combining the two reactances together, the phase difference/relationship between voltage and current of course starts to change a lot and depends on the "strength" of each of those components. Using a so called phasor or vector diagram that consists of 3 vectors; one for each voltage; we get that:
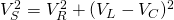
All this because inductive and capacitive voltage are vectors on the same axis that point in different directions and resistive voltage points in the other axis. The total sum of voltage is therefore a Parallelogram vector addition.
The AC version of Ohm's law using the complex resistance of Impedance is:
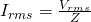
From this equation we can calculate the equation of impedance as being:

This final equation gives us the total impedance of an R-L-C circuit. When some components is missing we can "take out" the corresponding part of the equation. This same equation can also be calculated using a so called Impedance triangle, which consists of three vectors that correspond to the two reactances and the resistance.
Application
Consider an R-L-C circuit that consists of:
- a resistor of resistance R = 10Ω
- an inductor of inductance L = 5H
- a capacitor of capacitance C = 3F
- a voltage supply of voltage V = 7V, frequency f = 4Hz and no (extra) phase angle
Calculate:
- the reactance of each component
- the total impedance of the circuit
- the average (rms) voltage and current of the circuit
1.
The reactance of the inductor is:
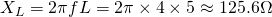
The reactance of the capacitor is:
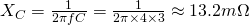
2.
The total impedance of the circuit is:
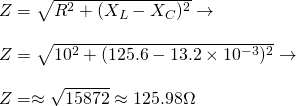
3.
The average/rms voltage of the circuit is:
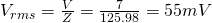
Using Ohm's law we can find the average current as:
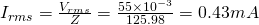
AC Power
Electrical power is the "rate" at which electrical energy is being convereted into heat inside of the resistor. In purely resistive circuits (both DC and AC) the instantanoues power is given by the equivalent (using Ohm's law) equations:
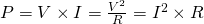
From this equation we see that ushc power exists only in closed-circuit, where both current and voltage are present. In AC circuits we will see that some other form of power (reactive) exists even in open-circuit conditions.
The instantaneous power in AC circuits is still P = VxI, but of course time-varying, the same way as current and voltage are. Of course current and voltage are affected by reactive components. The same happens to power! In AC circuits, power is being absorbed, stored and returned back. The phase differences make the equations of instantaneous and average power much more complex.
For purely resistive circuits the maximum instantaneous power is:
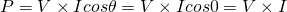
cause V and I have a 0° phase angle. The average or effective power can be calculated using the rms values as being:
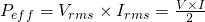
Purely reactive circuits of course have a "real" power magnitude of zero as no energy is being dissipated. But, we can still define an "imaginary" power that we call reactive power. The reactive power of an conductor is for example:
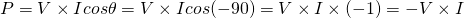
and so exactly the opposite to the "real" power of a purely resistive circuit, which shows us that a capacitor somehow produces energy. Of course a capacitor just returns back the energy it stored from the supply and doesn't produce actual "new" energy.
Mixing all the components together we start talking about the so called power factor. Reactive power Q = I^2X and real power P = I^2R together form the so called Apparent power S = I^2Z.
The total apparent power is equal to:
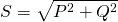
That can be found using the Pythagora theorem on the so called Power Triangle.
The power factor is being defined as the quotient of real with apparent power:
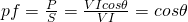
and is equal to the phase difference between current and voltage.
The power factor has a value between o.0 (purely reactive circuit where no energy is being lost) and 1.0 (purely resistive circuit where all the energy is being dissipated in the resistors) and so in the range [0.0, 1.1].
The voltage and current in R-L-C circuits are out of phase by a value in the range of [0, 90] degrees.
Application
Consider the circuit of the previous application...
Let's calculate:
- the effective/average apparent power S.
- the power factor (pf)
1.
Using the RMS voltage and current we get that:
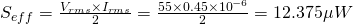
Note that the rms values where calculated using the total impedance, which means that the total effect of both real and reactive power was being considered.
2.
The power factor is equal to the phase difference/angle and so can be calculated easily using some trigonometry on top of the impedance triangle as:
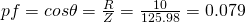
which shows us that the circuit is mostly reactive in nature.
The trigonometric equations about the phase angle φ that can be found from the impedance triangle are:

Resonance in Series R-L-C circuits
In series R-L-C circuits that total/sum voltage is:
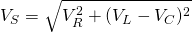
The impedance of such a series circuit is:
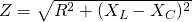
or even
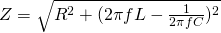
When the two reactances are equal to each other (XC = XL) we say that we are at series resonance. The resonance frequency at this point is:

During that series resonance the total phase angle is of course 0, cause VL = -VC, turning the circuit into a purely resistive circuit (pf = cos0 = 1). At resonance frequency the impedance Z is minimum, making the current maximum (Imax = V/R).
Application
Let's calculate:
- the resonance frequency AND
- maximum current
of the circuit that we had on the previous applications.
1.
The resonance frequency is:

2.
The maximum current is:
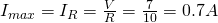
Resonance in Parallel R-L-C circuits
Parallel R-L-C circuits consist of the same components but connected in parallel, which means that the components have the same voltage, but different current. Therefore:
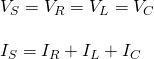
For such circuits we define a so called Current triangle (similar to the Voltage triangle of series circuits). From this triangle using Pethagora's theorem we get that:

This shows us that the total impedance is:

To make the analysis simpler we use the "opposite" of impedance, which is called admittance (Y). The admittance shows us the "ease" at which current flows through the circuit. In the same way we also define the opposite of reactance as conductance G, and the opposite of reactance as suspectance B. From the Admittance triangle (similar to the impedance triangle) we get:

The power factor / phase angle in such circuits is given by:

The resonance frequency in such circuits is the same as with series (having BL = BC this time) that can be found easily following the steps:
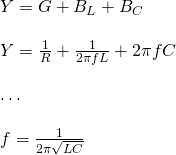
At parallel resonance (frequency) we define a maximum dynamic impedance:
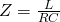
Application
Consider the same circuit that we talked about till now in our applications, but that it's in parallel connection.
Let's calculate:
- the Admittance of the circuit
- the maximum dynamic impedance
1.
At resonance frequency f the Admittance is:
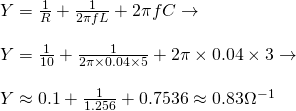
2.
The maximum dynamic impedance is:
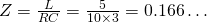
AC Transformers
Transformers transfer electric power from one electric circuit to another, without changing the frequency and most importantly without generating "new" energy. They consist of an input connetion, an output connection, mostly two windings and a laminated core. Their purpose is to change the voltage and current. The ratio between output and input voltage is equal to the number of turns between the two windings:
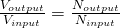
when talking about voltage transformers, giving the following equation for the output voltage:
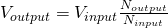
There are lots and lots of configurations and types of such AC transformers. The most important thing is the so called "turns ratio" (TR):
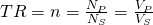
For current transformers this ratio is:
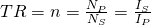
giving the following output (secondary) current equation:
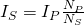
For all types we define the so called transformer EMF equation which can be found using Faraday's Induction law as:
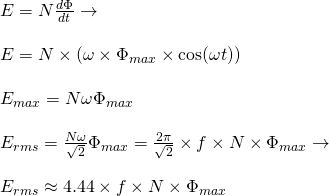
From this equation we can clearly see that transformers DO NOT operate on steady state DC voltages, but only in AC.
The Tranformer's power efficiency (η) is calculated by:

The total output wattage W is:
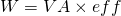
where:
- VA are the primary watts or volt-amps
- eff the secondary or effective watts
Example 1
Let's consider a transformer with:
- 10V primary or input voltage
- 25 turns in the primary winding
Calculate:
- the number of turns on the secondary winding AND
- the turns ratio (TR)
if we want an output voltage of 20V.
1.
From the ratio we we have that:

2.
TR is:
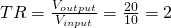
Example 2
Let's consider an transfomer with:
- N = 15 turns
- Φmax = 50mWb
- AC frequency f = 10Hz
- η = 85%
Calculate:
- the rms energy of the transformer (effective power)
- the input power (VA) of the transformer
- the total wattage of the transformer
1.
The rms energy can be calculated easily from:

2.
Knowing the power efficiency we can find the input power easily from:
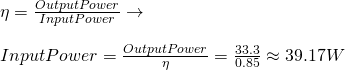
3.
Combining the two calculated energy and power values we get that the total wattage of the transformer is:
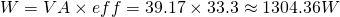
REFERENCES:
- The previous articles of the series with mathematical applications by myself
Mathematical equations that I had in this post where drawn using quicklatex!
Previous articles of the Electromagnetism series
Here we only have the previous two "chapters" and the current one....
Electromagnetic Induction:
Electromagnetic Induction and Faraday's law -> Electromagnetic Induction, Experiments, Faraday's law
Motional Electromotive Force (Emf) -> Motional Emf, Faraday's law and motional emf, generalization
Lenz's law and Induced Electric fields -> Lenz's law, Induced Electric Fields
Eddy Currents and Applications -> Εddy currents, applications (brakes, testing, others)
Maxwell's equations -> What they are, each equation analyzed separately
Electromagnetic Induction exercises -> examples all around Electromagnetic Induction
Mutual and Self Induction:
Mutual Inductance -> Mutual Inductance, applications
Self Induction -> Self Induction, Lenz's law, Inductance of a Coil
Magnetic Energy Density -> Energy stored in a magnetic field (or inductor), Magnetic energy density, Coaxial Cable Inductance Example
R-L circuits -> R-L circuit energizing, de-energizing, Characteristic time constant
L-C circuits -> L-C circuit, oscillations, energy cases, applications
R-L-C circuits -> R-L-C circuit, oscillation, applications
Mutual and Self Induction exercises -> examples all around Mutual and Self Induction
Alternating current:
Getting into Alternating current -> Phasor diagrams, Alternating current, Average (RMS) current and voltage, Differences, Advantages/Disadvantages
Electric Reactance in AC circuits -> Resistors, Inductor and Capacitor Reactance in AC circuits
Series R-L-C circuits Impedance -> Series R-L-C circuits, Phasor Diagrams, Impedance
Power in AC circuits -> DC Resistive circuit, Power in AC circuits (resistive, reactive), Power Factor
Resonance in Series R-L-C circuits -> Series R-L-C circuit, Series Resonance
Resonance in Parallel R-L-C circuits -> Parallel R-L-C circuit, Parallel Resonance
AC Transformers -> How they work, Configurations, Types, Voltage and Current Transformer
Final words | Next time
And this is actually it for today's post! Next time we will get into the final Electromagnetism topic. This final topic of course is Electromagnetic waves! After that topic I'm thinking of making a gigantic article that summarizes everything that we covered through-out the Electromagnetism branch!


Keep on drifting!
