[Image 1]
Introduction
Hey it's a me again @drifter1! Today we continue with the Physics branch "Classical Mechanics" to talk about Conservative and Non-Conservative Forces. The same way as last time, this article will continue theory and practice. With "practice" I mean examples/exercises around today's topics, so that you can understand everything better!
More specifcally, today's topics are:
- The Conservation of Energy
- Conservative Forces
- Non-Conservative Forces
- Conservative and Non-Conservative Fields
- Calculations and Exercises
So, without further ado, let's get straight into it!
The Conservation of Energy
First of all, "conservation" as a Physics term, refers to "something that doesn't change". Talking about a variable in an equation which represents a conserved quantity, that variable's equation/value is constant over time. This shows us that such quantitites have the same value before and after some event. Lots of quantities in Physics are being conserved and they are pretty useful for predictions in otherwise complicated situations. The three fundamental quantities, which are conserved when talking about Mechanics are:
- Energy
- Momentum
- Angular Momentum
More specifically for Energy we refer to the total energy of a system. When objects move around over time, the energy might change forms (kinetic, potential, heat), but it is conserved, meaning that the total remains the same. This conservation only applies to isolated systems, which don't interact with their surroundings.
But, what exactly do we mean by a system?
In physics, a system is a collection of objects that we choose to model with our equations. Everytime we want to describe the motion of an object using conservation of energy, we have to include the actual object of interest and all the other objects that interact with it. Anything that we don't include is usually collectively determined as "environment". Ignoring some of that environment will of course make our calculations less accurate. You have to describe the system knowing which effects can be safely ignored.
More about conservation of energy will be covered in articles to follow...
Conservative Forces
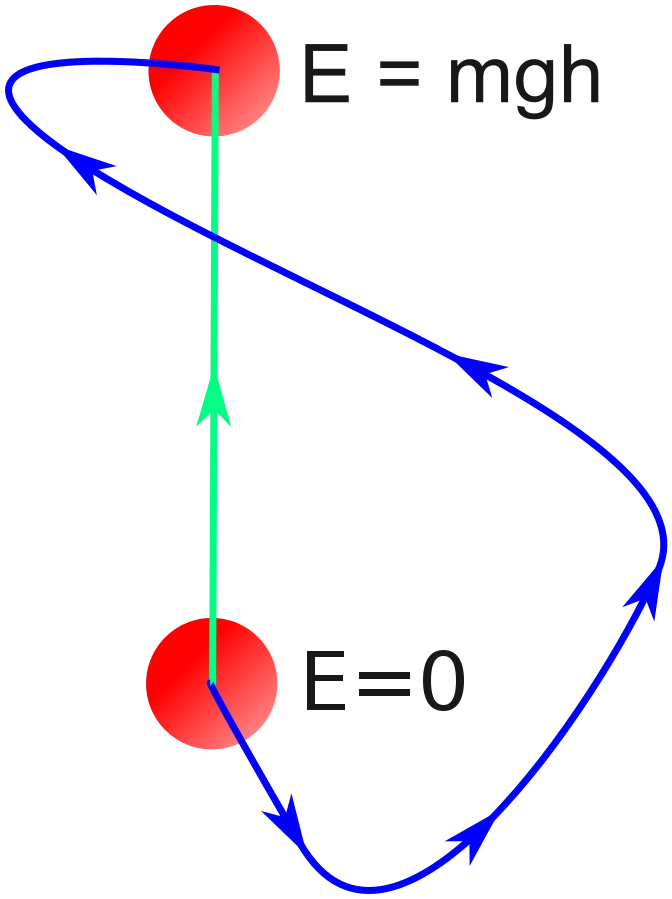
When talking about Conservative Forces you have to remember that the work of such a force on an object is path-independent. What really matters is the initial and final position of that path. Such forces are much easier to work with in physics cause the don't "leak" energy. Let's say that we start from a specific place and end up back on that same place. In that case we will have the same amount of energy as before, cause no energy is being "lost". That's why we say that the work done by such forces in a close path is zero. We also say that such forces "store energy" in a way.
Conservative force examples are:
- Gravitational forces
- Magnetic force
- Electrostatic force
- Elastic spring force
- Electric force
Let's now get into mathematical equations about conservative forces.
Knowing that the work done is path-independent we can write the following:
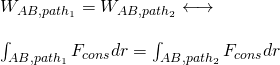
The work around any closed path is zero:
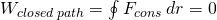
From the Work-Energy Theorem we can derive that the infinitesimal net work is equal to the exact differential of the kinetic energy, as following:
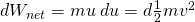
When talking about a two-dimensional force, or more specifically it's exact differential:
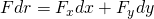
Following condition must apply for it to be conservative:
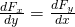
You might remember this condition from differential equations!
An example for a 3-dimensonal force can be found by the end of the following article, in the "optional section":
So, to summarize, what you have to remember is:
- The work done by such a force depends only on the initial and final position of the body and not on the actual path followed
- The work done around a closed path is zero
Non-Conservative Forces
When talking about Non-Conservative Forces the actual path matters. A great example of such a force is friction. A longer path will dissipate more kinetic energy than a short one, which clearly shows us that friction (and a non-conservative force in general) is path-dependent. Also, think about the heat that is dissipated into the environment. This dissipation happens so quickly, making heat energy unrecoverable and non-convertible. Such forces are clearly removing energy from the system, making it no longer available to the system. The energy does not disappear completely, but it just goes "somewhere else". What matters for us is that it doesn't "belong" to the system anymore.
Non-Conservative force examples are:
- Frictional forces
- Viscous forces
- Induction forces
- Air resistance force
- Tension in a string
- Normal force
- Propulsion force of a rocket or boat
So, to summarize, what you have to remember is:
- The work done by such a force depends on the path followed by the body
- The work done around a closed path is not zero.
Conservative and Non-Conservative Fields
In the same notion we can also talk about force fields, which can also be conservative or non-conservative. Let's suppose a non-uniform force-field f(r) that acts upon an object moving along a curved trajectory (path 1) from point A to point B. Let's also suppose a different trajectory (path 2) between the same points.
The work done by the force-field for each case/path is:
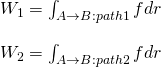
Now there are two possibilities:
- The Line-Integrals depend on the end points, A and B, but not on the path taken between them, in which case W1 = W2. [conservative force-field]
- The Line-Integrals depend both on the end points, A and B, and on the path taken between them, in which case W1 ≠ W2. [non-conservative force-field]
Another way of finding this out is by finding the integral along a closed circuit. Let's consider that the object move from point A to point B along path 1, and then from point B pack to point A along path 2. From the definition of line-integrals we know that we can simply reverse the path by picking up a minus sign. This shows us that:
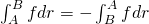
But, in the above integrals we simple took opposite directions along the same path! The total work done in a closed path is simply:
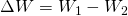
We again have two cases:
- For the case of a conservative field we have W1 = W2, for which we conclude that ΔW = 0
- For non-conservative fields we have W1 ≠ W2, for which we conclude that ΔW ≠ 0
We can see that the net work done by a conservative field on an object around a closed loop is zero, showing us that such a field stores energy without loss. In the second case the non-conservative field dissipates energy, making the object "give up" a certain amount of energy whil traveling.
Calculations and Exercises
Let's now lastly also get into some more specific examples!
Conservative Force (Example 8.2.1 of [5])
Let's consider the following two-dimensional forces:

Which of them are conservative and which are not? Assume that a and b are constants.
We have to check the condition for all three cases:
1.
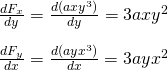
We can see that the two terms are not equal and so the force is non-conservative.
2.
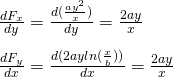
The terms are equal, meaning that the force is conservative.
3.
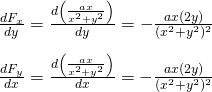
Again equal and so conservative.
Non-Conservative Force (Example 1 from [8])
Consider a baseball player sliding to stop on level ground. Using energy considerations, calculate the distance travelled by the 65.0-Kg baseball player, knowing that his initial speed is 6 m/s and that the friction against him is constant with a magnitude of 450N.
Solution
We know that the friction stops the player by converting his kinetic energy into other forms (including heat/thermal energy). In terms of the Work-Energy Theorem we can say that the work done by friction is negative, reducing the kinetic energy to zero. Friction f is applied in the opposite direction of the motion (θ = 180° or cosθ = -1). Therefore we have that W = -fd.
The last equation gives us:
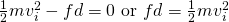
We know all the quantities except d (distance), meaning that we can solve it for d:

RESOURCES:
References
- https://www.khanacademy.org/science/physics/work-and-energy/work-and-energy-tutorial/a/what-is-conservation-of-energy
- https://www.dummies.com/education/science/physics/conservative-and-nonconservative-forces-in-physics/
- http://www.batesville.k12.in.us/physics/PhyNet/Mechanics/Energy/stored_energy.htm
- https://physicsabout.com/conservative-and-non-conservative-forces/
- https://phys.libretexts.org/TextBooks_and_TextMaps/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_I_-_Mechanics%2C_Sound%2C_Oscillations%2C_and_Waves_(OpenStax)/8%3A_Potential_Energy_and_Conservation_of_Energy/8.2%3A_Conservative_and_Non-Conservative_Forces
- http://farside.ph.utexas.edu/teaching/301/lectures/node59.html
- https://www.real-world-physics-problems.com/conservative-force.html
- https://courses.lumenlearning.com/physics/chapter/7-5-nonconservative-forces/
Images
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
- Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
You can find most of my previous articles organized per category, per series, per chapter, per article, in my recap of Summer 2018!
Final words | Next up
This is actually it for today's post! Next up is Potential Energy, for which we have lots and lots of things to cover, meaning that it might take more than one article to complete this topic.
See ya!


Keep on drifting!

